4. Median of Two Sorted Arrays(2个有序数组的中位数)
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
Example 1:
nums1 = [1, 3] nums2 = [2] The median is 2.0
Example 2:
nums1 = [1, 2] nums2 = [3, 4] The median is (2 + 3)/2 = 2.5
假设我们要找第 7 小的数字。

我们比较两个数组的第 k / 2 个数字,如果 k 是奇数,向下取整。也就是比较第 3 个数字,上边数组中的 4 和 下边数组中的 3 ,如果哪个小,就表明该数组的前 k / 2 个数字都不是第 k 小数字,所以可以排除。也就是 1,2,3 这三个数字不可能是第 7 小的数字,我们可以把它排除掉。将 1349 和 45678910 两个数组作为新的数组进行比较。
更一般的情况 A [ 1 ],A [ 2 ],A [ 3 ],A [ k / 2] ... ,B[ 1 ],B [ 2 ],B [ 3 ],B[ k / 2] ... ,如果 A [ k / 2 ] < B [ k / 2 ] ,那么 A [ 1 ],A [ 2 ],A [ 3 ],A [ k / 2] 都不可能是第 k 小的数字。
A 数组中比 A [ k / 2 ] 小的数有 k / 2 - 1 个,B 数组中,B [ k / 2 ] 比 A [ k / 2 ] 小,假设 B [ k / 2 ] 前边的数字都比 A [ k / 2 ] 小,也只有 k / 2 - 1 个,所以比 A [ k / 2 ] 小的数字最多有 k / 2 - 1 + k / 2 - 1 = k - 2 个,所以 A [ k / 2 ] 最多是第 k - 1 小的数。而比 A [ k / 2 ] 小的数更不可能是第 k 小的数了,所以可以把它们排除。
橙色的部分表示已经去掉的数字。
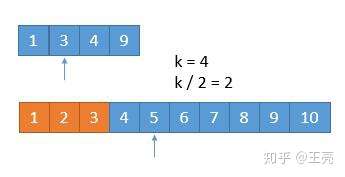
由于我们已经排除掉了 3 个数字,就是这 3 个数字一定在最前边,所以在两个新数组中,我们只需要找第 7 - 3 = 4 小的数字就可以了,也就是 k = 4 。此时两个数组,比较第 2 个数字,3 < 5,所以我们可以把小的那个数组中的 1 ,3 排除掉了。
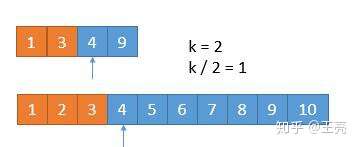
我们又排除掉 2 个数字,所以现在找第 4 - 2 = 2 小的数字就可以了。此时比较两个数组中的第 k / 2 = 1 个数,4 == 4 ,怎么办呢?由于两个数相等,所以我们无论去掉哪个数组中的都行,因为去掉 1 个总会保留 1 个的,所以没有影响。为了统一,我们就假设 4 > 4 吧,所以此时将下边的 4 去掉。
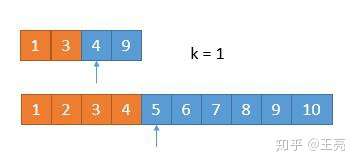
由于又去掉 1 个数字,此时我们要找第 1 小的数字,所以只需判断两个数组中第一个数字哪个小就可以了,也就是 4 。
所以第 7 小的数字是 4 。
我们每次都是取 k / 2 的数进行比较,有时候可能会遇到数组长度小于 k / 2 的时候。
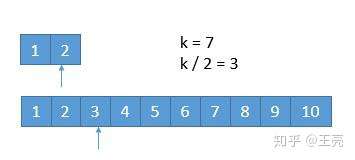
此时 k / 2 等于 3 ,而上边的数组长度是 2 ,我们此时将箭头指向它的末尾就可以了。这样的话,由于 2 < 3 ,所以就会导致上边的数组 1,2 都被排除。造成下边的情况。

由于 2 个元素被排除,所以此时 k = 5 ,又由于上边的数组已经空了,我们只需要返回下边的数组的第 5 个数字就可以了。
从上边可以看到,无论是找第奇数个还是第偶数个数字,对我们的算法并没有影响,而且在算法进行中,k 的值都有可能从奇数变为偶数,最终都会变为 1 或者由于一个数组空了,直接返回结果。
所以我们采用递归的思路,为了防止数组长度小于 k / 2 ,所以每次比较 min ( k / 2,len ( 数组 ) ) 对应的数字,把小的那个对应的数组的数字排除,将两个新数组进入递归,并且 k 要减去排除的数字的个数。递归出口就是当 k = 1 或者其中一个数字长度是 0 了。
对于一个长度为n的已排序数列a,若n为奇数,中位数为a[n / 2 + 1] ,
若n为偶数,则中位数(a[n / 2] + a[n / 2 + 1]) / 2
如果我们可以在两个数列中求出第K小的元素,便可以解决该问题
不妨设数列A元素个数为n,数列B元素个数为m,各自升序排序,求第k小元素(k=m+n)
取A[k / 2] B[k / 2] 比较,
如果 A[k / 2] > B[k / 2] 那么,所求的元素必然不在B的前k / 2个元素中(证明反证法)
反之,必然不在A的前k / 2个元素中,于是我们可以将A或B数列的前k / 2元素删去,求剩下两个数列的
k - k / 2小元素,于是得到了数据规模变小的同类问题,递归解决
如果 k / 2 大于某数列个数,所求元素必然不在另一数列的前k / 2个元素中,同上操作就好。
需要尝试对两个数组同时进行二分查找,逐步排除掉不可能出现中位数的区间,最后找到所求的中位数。这种解法的主要思想就是:
如果数组a的中位数小于数组b的中位数,那么整体的中位数只可能出现在a的右区间加上b的左区间之中;
如果数组a的中位数大于等于数组b的中位数,那么整体的中位数只可能出现在a的左区间加上b的右区间之中。
关键就是利用分治的思想逐渐缩小a的区间和b的区间来找到中位数。
1 class Solution { 2 public double findMedianSortedArrays(int[] nums1, int[] nums2) { 3 double res = 0.0; 4 int n = nums1.length; 5 int m = nums2.length; 6 if((m+n)%2==1) 7 res = (double)kth(nums1,nums2,0,0,(m+n+1)/2); 8 else 9 res = (double) ( kth(nums1,nums2,0,0,(m+n)/2) + 10 kth(nums1,nums2,0,0,(m+n)/2+1))/2; 11 return res; 12 13 } 14 private int kth(int[] a,int[] b,int alo,int blo,int k){ 15 if(alo>=a.length) return b[blo+k-1]; 16 if(blo>=b.length) return a[alo+k-1]; 17 if(k==1) return Math.min(a[alo],b[blo]); 18 19 int aMid = Integer.MAX_VALUE, bMid = Integer.MAX_VALUE; 20 21 if(alo+k/2-1<a.length) 22 aMid = a[alo+k/2-1]; 23 if(blo+k/2-1<b.length) 24 bMid = b[blo+k/2-1]; 25 26 if(aMid>bMid) 27 return kth(a,b,alo,blo+k/2,k-k/2); 28 else 29 return kth(a,b,alo+k/2,blo,k-k/2); 30 } 31 }



