动态规划相关
字符串子序列
300. Longest Increasing Subsequence(LIS最长递增子序列 动态规划)
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
状态转移方程
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意这里不是要dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值。
输入:nums = [1,3,5,4,7] 输出:3 解释:最长连续递增序列是 [1,3,5], 长度为3。
dp[i]:以下标i为结尾的数组的连续递增的子序列长度为dp[i]。注意这里的定义,一定是以下标i为结尾,并不是说一定以下标0为起始位置。
确定递推公式
如果 nums[i + 1] > nums[i],那么以 i+1 为结尾的数组的连续递增的子序列长度 一定等于 以i为结尾的数组的连续递增的子序列长度 + 1 。
即:dp[i + 1] = dp[i] + 1;
因为本题要求连续递增子序列,所以就必要比较nums[i + 1]与nums[i],而不用去比较nums[j]与nums[i] (j是在0到i之间遍历)。
既然不用j了,那么也不用两层for循环,本题一层for循环就行,比较nums[i + 1] 和 nums[i]。
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
dp[i]:包括下标i之前的最大连续子序列和为dp[i]。
dp[i]只有两个方向可以推出来:
- dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和
- nums[i],即:从头开始计算当前连续子序列和
一定是取最大的,所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
718. 最长重复子数组(dp) (双字符串)
1143. 最长公共子序列(dp) (双字符串)
392. 判断子序列(双指针\dp) (双字符串)
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
示例 1: 输入:s = "abc", t = "ahbgdc" 输出:true
示例 2: 输入:s = "axc", t = "ahbgdc" 输出:false
dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。
- if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
- if (s[i - 1] != t[j - 1])
- 相当于t要删除元素,继续匹配
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在dp[i-1][j-1]的基础上加1(如果不理解,在回看一下dp[i][j]的定义)

dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
这一类问题,基本是要分析两种情况
- s[i - 1] 与 t[j - 1]相等
- s[i - 1] 与 t[j - 1] 不相等
当s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。
一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
这里可能有同学不明白了,为什么还要考虑 不用s[i - 1]来匹配,都相同了指定要匹配啊。
例如: s:bagg 和 t:bag ,s[3] 和 t[2]是相同的,但是字符串s也可以不用s[3]来匹配,即用s[0]s[1]s[2]组成的bag。
当然也可以用s[3]来匹配,即:s[0]s[1]s[3]组成的bag。
72. Edit Distance(编辑距离 动态规划) (双字符串)
5. Longest Palindromic Substring(最长回文子串 manacher 算法/ DP动态规划)
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
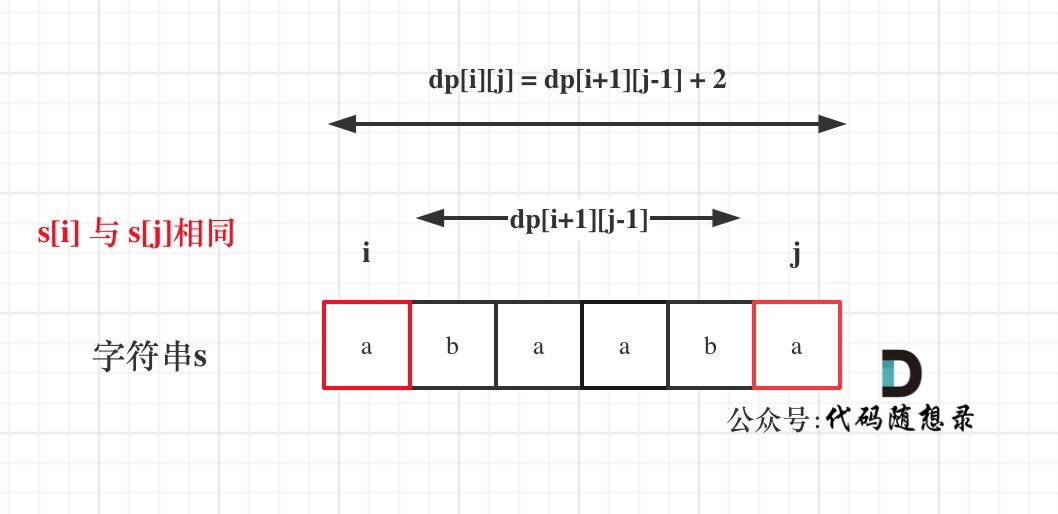
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
30连续子数组的最大和
97. Interleaving String(字符串的交替连接 动态规划)
路径题:
62. Unique Paths (走棋盘多少种不同的走法 动态规划)
63. Unique Paths II(有障碍的路径 动态规划)



