5. Longest Palindromic Substring

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example:

Input: "babad"

Output: "bab"

Note: "aba" is also a valid answer.

 

Example:

Input: "cbbd"

Output: "bb"

 

动态规划

此题还可以用动态规划Dynamic Programming来解，我们维护一个二维数组dp，其中dp[i][j]表示字符串区间[i, j]是否为回文串，当i = j时，只有一个字符，肯定是回文串，如果i = j + 1，说明是相邻字符，此时需要判断s[i]是否等于s[j]，如果i和j不相邻，即i - j >= 2时，除了判断s[i]和s[j]相等之外，dp[j + 1][i - 1]若为真，就是回文串，通过以上分析，可以写出递推式如下：

dp[i, j] = 1                                               if i == j

           = s[i] == s[j]                                if j = i + 1

           = s[i] == s[j] && dp[i + 1][j - 1]    if j > i + 1      

 

 

 

class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        res = ''
        dp = [[False] * n for _ in range(n)]
        for i in range(n):
            dp[i][i] = True
        for i in range(n)[::-1]:
            for j in range(i,n):
                if s[i]==s[j]:
                    if j-i <=2:
                        dp[i][j] = True
                    else:
                        dp[i][j] = dp[i+1][j-1]
                if dp[i][j] and j-i >=len(res):
                    res = s[i:j+1]
        return res 

 

 

 

 

 

中心扩散法：

 

class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        res = ""
        for index in range(n):
            ##
            l = r = index
            while l >= 0 and r < n and s[l] == s[r]:
                l-=1
                r+=1
            if r-l-1 > len(res):
                res = s[l+1:r]
            ####
            l = index
            r = index + 1
            while l >= 0 and r < n and s[l] == s[r]:
                l-=1
                r+=1
            if r-l-1 > len(res):
                res = s[l+1:r]
        return res

 

 

class Solution {
public:
    vector<int> find(string& s, int low, int high) {
        vector<int> res(2,0);
        while(low>=0 && high<s.size() && s[low]==s[high]) {
            low--;
            high++;
        }
        res[0] = low+1;
        res[1]  = (high-1)-(low+1);
        return res;
    }
    string longestPalindrome(string s) {
        int n = s.size();
        int max_len_start = 0;
        int max_len = 0;
        for(int i = 0; i<n;++i) {
            vector<int> res1 = find(s,i,i);
            vector<int> res2 = find(s,i,i+1);

            int cur_max_start =  res1[1]>res2[1]? res1[0]:res2[0];
            int cur_max = res1[1]>res2[1]? res1[1]:res2[1];

            if (cur_max>max_len) {
                max_len = cur_max;
                max_len_start = cur_max_start;
            }
        
        }
        return s.substr(max_len_start,max_len+1);
    }
};

 

 

 

 manacher 算法

回文有奇数偶数的问题，所以加上gap,这样字符串一定是奇数,所以只考虑奇数匹配就行。

a b c -----> #a#b#c#

a b       -->#a#b#

 

 

 

1、预处理成上面的样子，为处理方便，在最前面加一个从未出现的字符$

 

2、建立数组P，P[i] 来记录字符S[i]为中心的最长回文子串向左/向右扩张的长度（包括S[i]）

 

例如：

12212321

预处理：$#1#2#2#1#2#3#2#1#

          P: 12125214121612121 

 

 

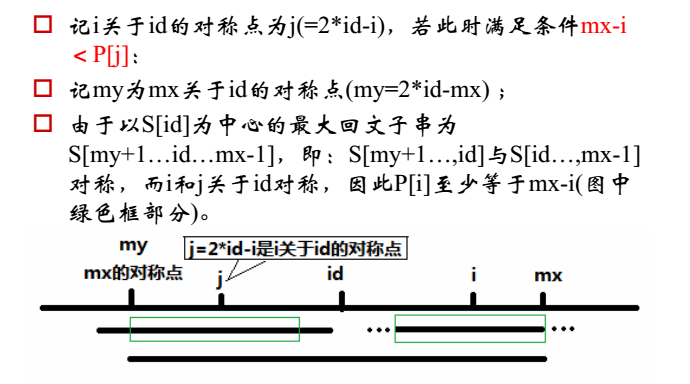
绿框之外的暴力

 

 

 1 class Solution:
 2     def longestPalindrome(self, s):
 3         """
 4         :type s: str
 5         :rtype: str
 6         """
 7         # preprocess
 8         slist = list(s)
 9         for i in range((len(s) + 1) * 2)[::2]:
10             slist.insert(i, "#")
11         slist.insert(0, '$')
12         
13         p = self.manacher(slist)
14         
15         i = p.index(max(p))
16         ans = ''.join(slist[i-p[i]+1:i+p[i]])
17         return ans.replace('#','').replace('$','')
18     def manacher(self, slist):
19    
20 
21         # 计算p
22         p = [0] * len(slist)
23         p[0] = 1
24         id = 0
25         mx = 1
26         print(slist)
27         for i in range(1,len(slist)):
28             if mx > i:
29                 p[i] = min(p[id * 2 - i], mx - i)
30             else:
31                 p[i] = 1
32 
33             #暴力
34             while i +p[i]<len(slist) and slist[i - p[i]]==slist[i + p[i]]:
35                 p[i] = p[i]+1
36             #更新最大三元组
37             if(mx < i + p[i]):
38                 mx = i + p[i]
39                 id = i
40 
41         return p