剑指Offer--35数组中的逆序对
题目描述
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
输入描述:
题目保证输入的数组中没有的相同的数字
数据范围:
对于%50的数据,size<=10^4
对于%75的数据,size<=10^5
对于%100的数据,size<=2*10^5
示例1
输
1,2,3,4,5,6,7,0
输出
7
class Solution: def reversePairs(self, nums: List[int]) -> int: def merge(nums,aux,l,m,r): i = l j = m k = l cnt = 0 while i < m and j < r : if aux[i] <= aux[j]: nums[k] = aux[i] i+=1 k+=1 else: nums[k] = aux[j] j+=1 k+=1 cnt += (m - i) while i < m : nums[k] = aux[i] i+=1 k+=1 while j < r : nums[k] = aux[j] j+=1 k+=1 aux[l:r] = nums[l:r] return cnt def merge_sort(nums,aux,l,r): if l>=r-1 : return 0 m = l + int((r-l)/2) a = merge_sort(nums,aux,l,m) b = merge_sort(nums,aux,m,r) c = merge(nums,aux,l,m,r) return a+b+c aux = nums.copy() return merge_sort(nums,aux,0,len(nums)) #return nums
思路:
类似于megersort
先统计子数组内部的逆序对的数目,然后再统计2个相邻子数组之间的逆序对的数目,在统计的过程中,还需要对数组排序,
排序可以避免重复统计。
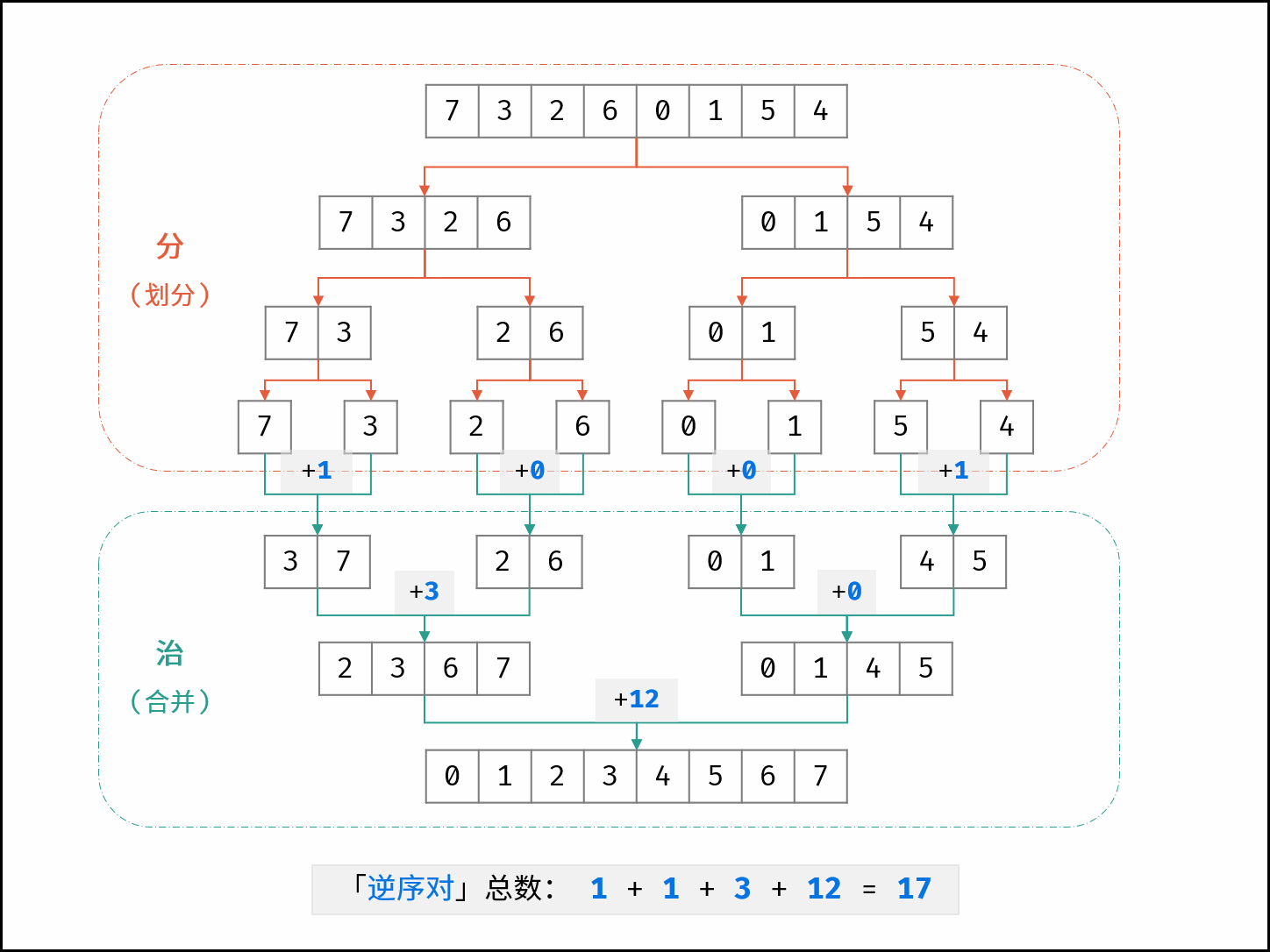
37 \ 26 合并的时候,
3 > 2, 所以2的逆序对有2个(32,72)
37与6合并的时候,逆序对有1个(76)
class Solution { public: int merge(vector<int>& nums,vector<int>&aux,int left, int mid, int right) { int l_start = left; int l_end = mid; int r_start = mid + 1; int r_end = right; int k = left; int cnt = 0; while(l_start<=l_end && r_start<=r_end) { if (nums[l_start] <= nums[r_start]) { aux[k++] = nums[l_start++]; } else { aux[k++] = nums[r_start++]; cnt += (mid - l_start +1);// 记录逆序对个数 } } while(l_start<=l_end) { aux[k++] = nums[l_start++]; } while(r_start<=r_end) { aux[k++] = nums[r_start++]; } // sort for(int k = left; k<= right;k++) { nums[k] = aux[k]; } return cnt; } int msort(vector<int>&nums,vector<int>&aux,int left, int right) { if(left>=right) return 0; int mid = left + (right - left) /2; int l = msort(nums,aux,left,mid); int r = msort(nums,aux,mid+1,right); int m = merge(nums,aux,left,mid,right); return l + r + m; } int reversePairs(vector<int>& nums) { vector<int> aux = vector<int>(nums.size()); return msort(nums,aux,0,nums.size()-1); } };
1 public class Solution { 2 public int InversePairs(int [] a) { 3 int[] aux = new int[a.length]; 4 for(int i = 0;i<a.length;i++) 5 aux[i] = a[i]; 6 7 return fun(a,aux,0,a.length-1); 8 } 9 private int fun(int[] a,int[] aux,int lo,int hi){ 10 if(lo==hi) return 0; 11 int mid = (hi-lo)/2+lo; 12 int left = fun(a,aux,lo,mid)%1000000007; 13 int right = fun(a,aux,mid+1,hi)%1000000007; 14 15 int i = mid; 16 int j = hi; 17 int ai = hi;//aux_index 18 int count = 0; 19 while(i>=lo&&j>=mid+1){ 20 if(a[i]>a[j]){ 21 aux[ai--] = a[i--]; 22 count+=j-mid; 23 if(count>=1000000007)//数值过大求余 24 count%=1000000007; 25 } 26 else 27 aux[ai--]=a[j--]; 28 } 29 30 while(i>=lo) 31 aux[ai--]=a[i--]; 32 while(j>=mid+1) 33 aux[ai--] =a[j--]; 34 35 //更新数组 36 for(int k = lo;k<=hi;k++) 37 a[k] = aux[k]; 38 39 return (left+right+count)%1000000007; 40 } 41 }
c++ 20180725
1 class Solution { 2 public: 3 int InversePairs(vector<int> data) { 4 int length = data.size(); 5 if(length<=0) return 0; 6 std::vector<int> copy(data); 7 long long cnt = InversePairsCore(data,copy,0,length-1); 8 return cnt; 9 } 10 long long InversePairsCore(std::vector<int> &data,std::vector<int> ©,int lo,int hi){ 11 if(lo==hi) return 0; 12 int mid = lo+(hi-lo)/2; 13 long long left = InversePairsCore(data,copy,lo,mid); 14 long long right =InversePairsCore(data,copy,mid+1,hi); 15 16 int i = mid; 17 int j = hi; 18 int k = hi; 19 int cnt = 0; 20 while(i>=lo&&j>=mid+1){ 21 if(data[i]>data[j]){ 22 copy[k--]=data[i--]; 23 cnt+=j-mid; 24 if(cnt>=1000000007) 25 cnt%=1000000007; 26 } 27 else{ 28 copy[k--]=data[j--]; 29 } 30 } 31 while(i>=lo) 32 copy[k--] = data[i--]; 33 while(j>=mid+1) 34 copy[k--] = data[j--]; 35 for(int m = lo;m<=hi;m++) 36 data[m] =copy[m]; 37 return (left+right+cnt)%1000000007; 38 } 39 };



