回归问题求解 python---梯度下降+最小二乘法

 

 

MSE = 1/m * ∑i=1m(yi−y^i)2

 

                                              
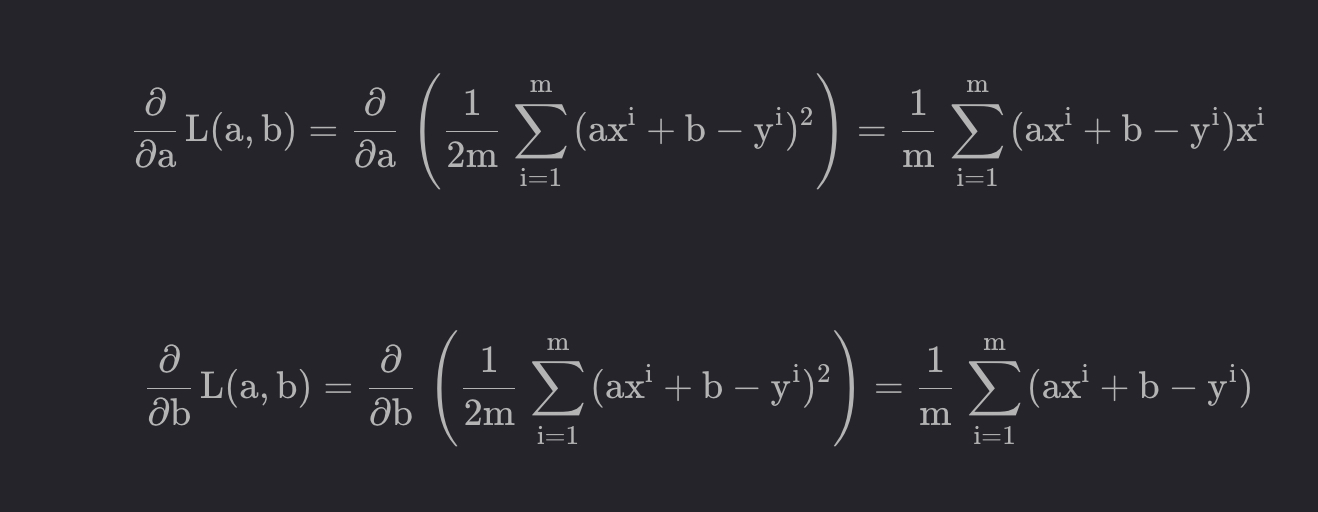
a = [1., 2., 3., 4., 5., 6., 7., 8., 9.]      
b = [3., 5., 7., 9., 11., 13., 15., 17., 19.] 
points = [[a[i],b[i]] for i in range(len(a))]

lr= 0.001
eps = 0.0001
m = len(points)
last_error = float('inf')
k = b = grad_k = grad_b = error = 0.0
for step in range(100000):
    error = 0.0  # 重新初始化误差为0
    for i in range(m):
        x,y = points[i]
        predict_y = x*k + b
        
        grad_k = (predict_y - y) * x  # 计算k的梯度
        grad_b = predict_y - y        # 计算b的梯度
        
        grad_k/=m
        grad_b/=m
        
        k-=grad_k*lr
        b-=grad_b*lr

        error += (predict_y - y) ** 2  # 累积误差

    if abs(last_error - error) < eps:
        break
    last_error = error

print('{0} * x + {1}'.format(k, b))

 

def liner_fitting(data_x,data_y):
      size = len(data_x);
      i=0
      sum_xy=0
      sum_y=0
      sum_x=0
      sum_sqare_x=0
      average_x=0;
      average_y=0;
      while i<size:
          sum_xy+=data_x[i]*data_y[i];
          sum_y+=data_y[i]
          sum_x+=data_x[i]
          sum_sqare_x+=data_x[i]*data_x[i]
          i+=1
      average_x=sum_x/size
      average_y=sum_y/size
      return_k=(size*sum_xy-sum_x*sum_y)/(size*sum_sqare_x-sum_x*sum_x)
      return_b=average_y-average_x*return_k
      return [return_k,return_b]