486. 预测赢家
给你一个整数数组 nums 。玩家 1 和玩家 2 基于这个数组设计了一个游戏。
玩家 1 和玩家 2 轮流进行自己的回合,玩家 1 先手。开始时,两个玩家的初始分值都是 0 。每一回合,玩家从数组的任意一端取一个数字(即,nums[0] 或 nums[nums.length - 1]),取到的数字将会从数组中移除(数组长度减 1 )。玩家选中的数字将会加到他的得分上。当数组中没有剩余数字可取时,游戏结束。
如果玩家 1 能成为赢家,返回 true 。如果两个玩家得分相等,同样认为玩家 1 是游戏的赢家,也返回 true 。你可以假设每个玩家的玩法都会使他的分数最大化。
示例 1:
输入:nums = [1,5,2] 输出:false 解释:一开始,玩家 1 可以从 1 和 2 中进行选择。 如果他选择 2(或者 1 ),那么玩家 2 可以从 1(或者 2 )和 5 中进行选择。如果玩家 2 选择了 5 ,那么玩家 1 则只剩下 1(或者 2 )可选。 所以,玩家 1 的最终分数为 1 + 2 = 3,而玩家 2 为 5 。 因此,玩家 1 永远不会成为赢家,返回 false 。
示例 2:
输入:nums = [1,5,233,7] 输出:true 解释:玩家 1 一开始选择 1 。然后玩家 2 必须从 5 和 7 中进行选择。无论玩家 2 选择了哪个,玩家 1 都可以选择 233 。 最终,玩家 1(234 分)比玩家 2(12 分)获得更多的分数,所以返回 true,表示玩家 1 可以成为赢家。
class Solution: def predictTheWinner(self, nums: List[int]) -> bool: #我们要求的结果其实就是两个选手的胜负,那么不用两个选手的得分,而是把问题转换为两个选手所拿元素的差值。 def backtracking(l,r): if l >r : return 0 a = nums[l] - backtracking(l+1,r) b = nums[r] - backtracking(l,r-1) return max(a,b) return backtracking(0,len(nums)-1) >= 0
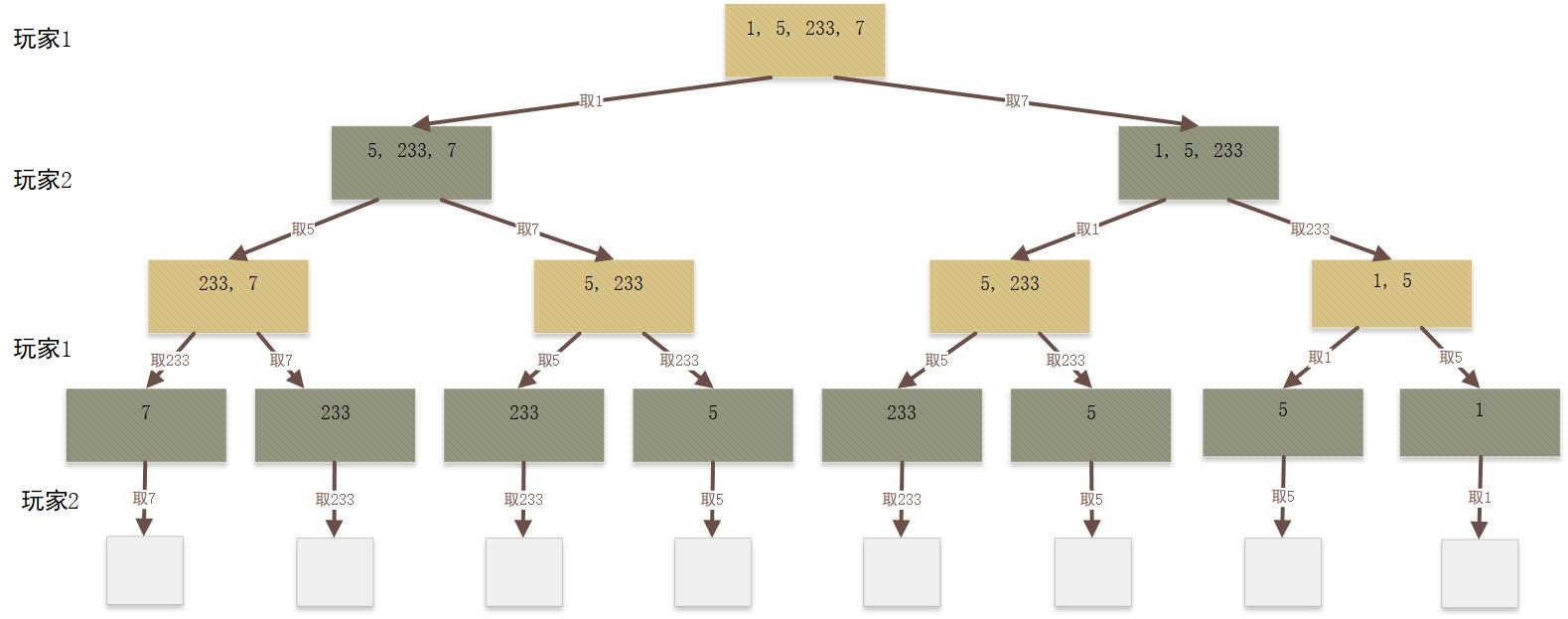
dfs: 第一个人得分综总和
class Solution { public: int dfs(vector<int>& nums, int i, int j) { if (i>j) return 0; if (i==j) return nums[i]; int a = nums[i] + min(dfs(nums,i+1,j-1), dfs(nums,i+2,j)); int b = nums[j] + min(dfs(nums,i+1,j-1), dfs(nums,i,j-2)); //cout << i << " " << j << " " << max(a,b) << endl; return max(a,b); } bool PredictTheWinner(vector<int>& nums) { int total = 0; for(auto a:nums) total+=a; int first = dfs(nums,0,nums.size()-1); return first >=total-first; } };
方法2: 因为就我们要求的结果其实就是两个选手的胜负,那么不用两个选手的得分,而是把问题转换为两个选手所拿元素的差值。
class Solution: def backtrackint(self,nums,i,j): if i>j: return 0 return max( nums[i]-self.backtrackint(nums,i+1,j), nums[j]-self.backtrackint(nums,i,j-1) ) def PredictTheWinner(self, nums: List[int]) -> bool: res = self.backtrackint(nums,0,len(nums)-1) return res >= 0
class Solution { public: int dfs(vector<int>& nums, int i, int j,vector<vector<int>>&dp) { if (i>j) return 0; if (i==j) return nums[i]; if (dp[i][j] != -1) return dp[i][j]; int a = nums[i] + min(dfs(nums,i+1,j-1,dp), dfs(nums,i+2,j,dp)); int b = nums[j] + min(dfs(nums,i+1,j-1,dp), dfs(nums,i,j-2,dp)); dp[i][j] = max(a,b); return dp[i][j]; } bool PredictTheWinner(vector<int>& nums) { int total = 0; int n = nums.size(); vector<vector<int>> dp(n,vector<int>(n,-1)); for(auto a:nums) total+=a; int first = dfs(nums,0,nums.size()-1,dp); return first >=total-first; } };


