310. 最小高度树 （拓扑排序 bfs）

 

树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。

 

示例 1：

输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：

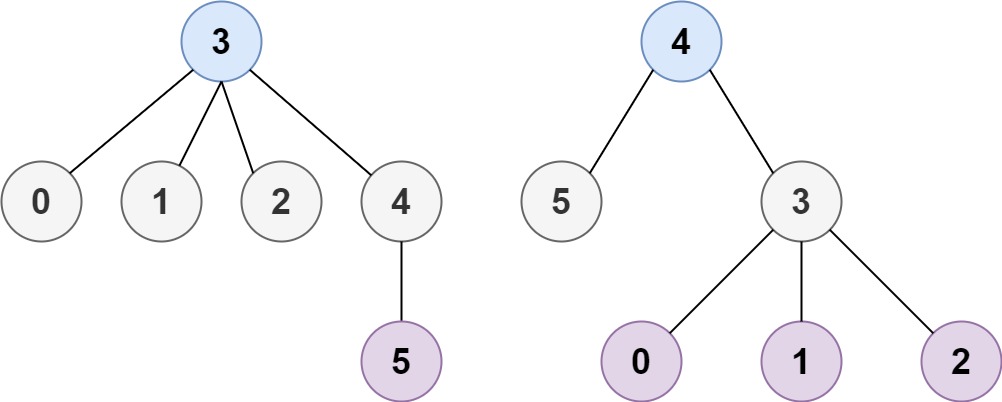
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

 

 

 

从叶子节点出发，一步步找到最终的根节点集合。

为什么从叶子节点出发就一定是正确的呢？

因为叶子节点永远在最外面，如果以叶子节点为根，那么树的高度为叶子+根+...+叶子，总是要高于根+...+叶子，所以从叶子节点出发到根才能得到最短高度。

基于BFS，每次都把当前的叶子节点遍历并剪枝，得到新的叶子节点放入队列中，直到无法剪枝，这时候队列中的节点即为最小高度树的根节点，代码如下：

 

 

 

 

class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        if (n ==1) return vector<int>(1,0);
        vector<int> degree(n,0);
        vector<vector<int>> tree(n);
        for(int i = 0; i < edges.size();i++) {
            degree[edges[i][0]]++;
            degree[edges[i][1]]++;
            tree[edges[i][0]].emplace_back(edges[i][1]);
            tree[edges[i][1]].emplace_back(edges[i][0]);
        }
        vector<int> res;
        queue<int> q;
        for(int i = 0; i < n;i++) {
            if (degree[i]==1) {
                q.push(i);
            }
        }
        while(!q.empty()) {
            int size = q.size();// bfs 需要记录层数，然后返回最后一层的结果
            res.clear();
            for(int i = 0;i < size; i++) {
                int top = q.front();
                q.pop();
                degree[top]--;
                res.emplace_back(top);
                for (int edge:tree[top]) {
                    degree[edge]--;
                    if (degree[edge] == 1) {
                        q.push(edge);
                    }
                }
            }
        }
        return res;
    }
};