84. 柱状图中最大的矩形 （双指针、单调栈）

 

难度困难1873

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

 

示例 1:

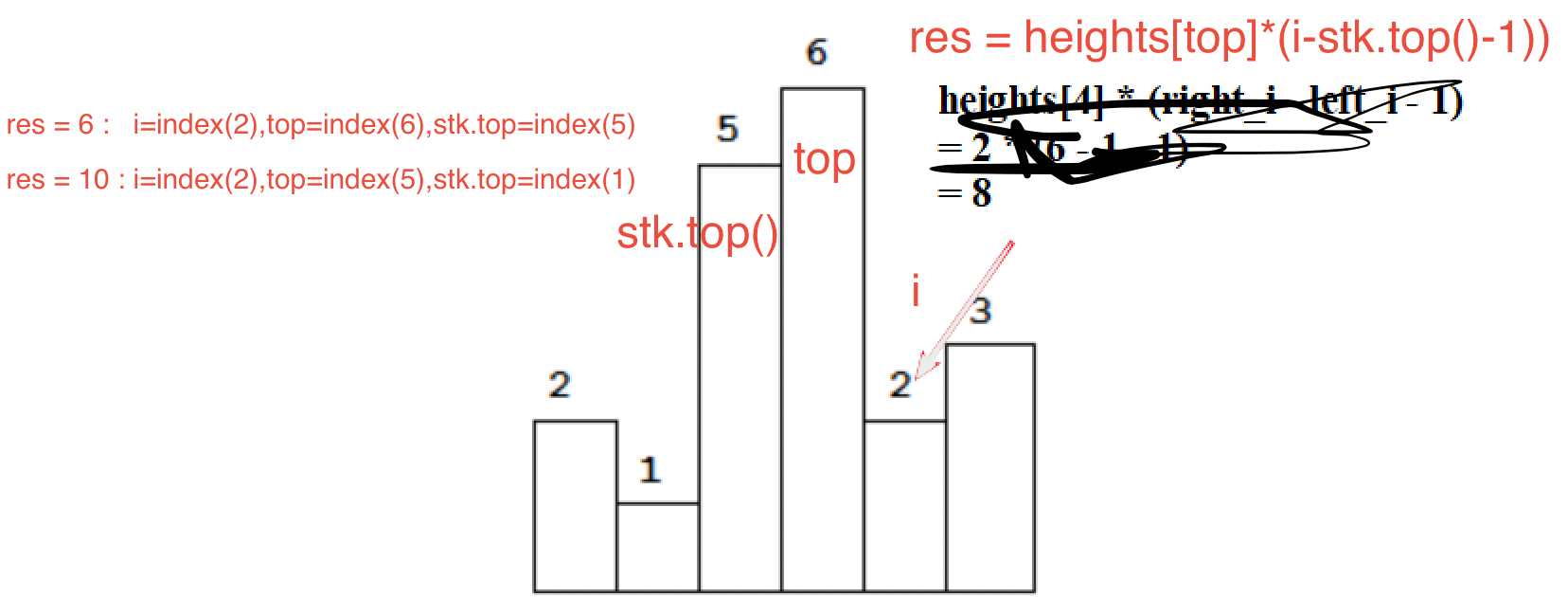
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

输入： heights = [2,4]
输出： 4

 

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        heights = [0] + heights + [0]
        stack = []
        res = 0
        for i in range(len(heights)):
            cur = heights[i]
            while stack and cur < heights[stack[-1]]:
                top = stack.pop()
                area = heights[top] * (i-stack[-1]-1)  #不是i-top 212这种过不了 
                res = max(res,area)
            stack.append(i)
        return res 

 

 

 

 

 

 

 

 

 

中心扩散，找到当前以 hight[i] 为高，长度最长，然后算 面积。 

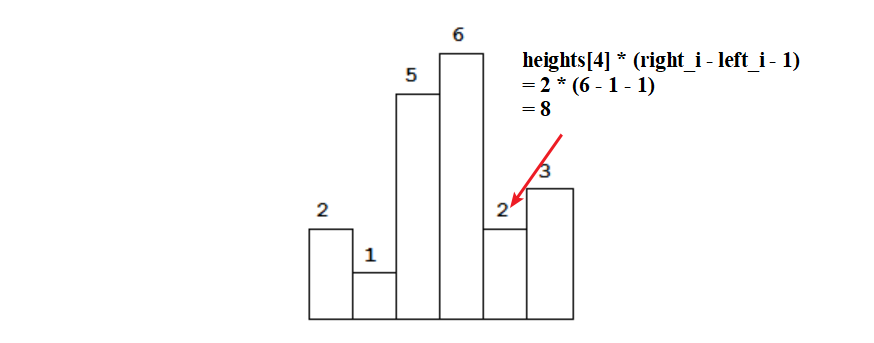
是以i 为中心，向左找第一个小于 heights[i] 的位置 left_i；向右找第一个小于于 heights[i] 的位置 right_i，即最大面积为 heights[i] * (right_i - left_i -1)，如下图所示：

所以，我们的问题就变成如何找 right_i 和 left_i？

 

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int max_res = 0;
        int n = heights.size();
        for (int i = 0; i < n;i++) {
            int left_i = i;
            while (left_i >= 0 && heights[left_i] >= heights[i]) left_i--;
            int right_i = i;
            while (right_i <= n-1 && heights[right_i] >= heights[i]) right_i++;
            max_res = max(max_res,heights[i] * (right_i-left_i-1)); 
            //cout << heights[i]  << "  "  << left_i << "  " << right_i << endl;
        }
        return max_res;
    }
};

 

 

2 3 4 1 为例子，

234 入栈，到1 时，无法入栈。 需要将栈内大于1的元素弹出，此时，以右边界就找到了，就是1所在的索引，4的左边界就是把4弹出来，剩下的 top 就是3 所在的索引，继续弹，只到弹完，就相当于遍历了以 1为右边界，所有的面积。

 

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        
        // 两端补0， 不然24 这种 case 过不了、
        // 单调递增栈
        // 2,1,5,6,2,3   
        //  stk = 1 5 6  i = 2
        // 以6为高， 右边界是2，左边界是5
        heights.insert(heights.begin(),0);
        heights.push_back(0);
        int res = 0;
        int top = 0;
        stack<int> stk;
        for(int i = 0; i < heights.size(); i++) {
            while(!stk.empty() && heights[i] < heights[stk.top()]) {
                top = stk.top();
                stk.pop();
                res = max(res, heights[top]*(i-stk.top()-1));
            }
            stk.push(i);          
        }
        return res;
    }