BFS
BFS :
BFS 的核心思想应该不难理解的,就是把一些问题抽象成图,从一个点开始,向四周开始扩散。一般来说,我们写 BFS 算法都是用「队列」这种数据结构,每次将一个节点周围的所有节点加入队列。
BFS 相对 DFS 的最主要的区别是:BFS 找到的路径一定是最短的,但代价就是空间复杂度可能比 DFS 大很多,至于为什么,我们后面介绍了框架就很容易看出来了。
本文就由浅入深写两道 BFS 的典型题目,分别是「二叉树的最小高度」和「打开密码锁的最少步数」,手把手教你怎么写 BFS 算法。
这个广义的描述可以有各种变体,比如走迷宫,有的格子是围墙不能走,从起点到终点的最短距离是多少?如果这个迷宫带「传送门」可以瞬间传送呢?
再比如说两个单词,要求你通过某些替换,把其中一个变成另一个,每次只能替换一个字符,最少要替换几次?
再比如说连连看游戏,两个方块消除的条件不仅仅是图案相同,还得保证两个方块之间的最短连线不能多于两个拐点。你玩连连看,点击两个坐标,游戏是如何判断它俩的最短连线有几个拐点的?
再比如……
净整些花里胡哨的,这些问题都没啥奇技淫巧,本质上就是一幅「图」,让你从一个起点,走到终点,问最短路径。这就是 BFS 的本质,框架搞清楚了直接默写就好。
1、为什么 BFS 可以找到最短距离,DFS 不行吗?
首先,你看 BFS 的逻辑,depth 每增加一次,队列中的所有节点都向前迈一步,这保证了第一次到达终点的时候,走的步数是最少的。
DFS 不能找最短路径吗?其实也是可以的,但是时间复杂度相对高很多。你想啊,DFS 实际上是靠递归的堆栈记录走过的路径,你要找到最短路径,肯定得把二叉树中所有树杈都探索完才能对比出最短的路径有多长对不对?而 BFS 借助队列做到一次一步「齐头并进」,是可以在不遍历完整棵树的条件下找到最短距离的。
形象点说,DFS 是线,BFS 是面;DFS 是单打独斗,BFS 是集体行动。这个应该比较容易理解吧。
2、既然 BFS 那么好,为啥 DFS 还要存在?
BFS 可以找到最短距离,但是空间复杂度高,而 DFS 的空间复杂度较低。
还是拿刚才我们处理二叉树问题的例子,假设给你的这个二叉树是满二叉树,节点数为 N,对于 DFS 算法来说,空间复杂度无非就是递归堆栈,最坏情况下顶多就是树的高度,也就是 O(logN)。
但是你想想 BFS 算法,队列中每次都会储存着二叉树一层的节点,这样的话最坏情况下空间复杂度应该是树的最底层节点的数量,也就是 N/2,用 Big O 表示的话也就是 O(N)。
由此观之,BFS 还是有代价的,一般来说在找最短路径的时候使用 BFS,其他时候还是 DFS 使用得多一些(主要是递归代码好写)。
双向 bfs:双向 BFS 也有局限,因为你必须知道终点在哪里。
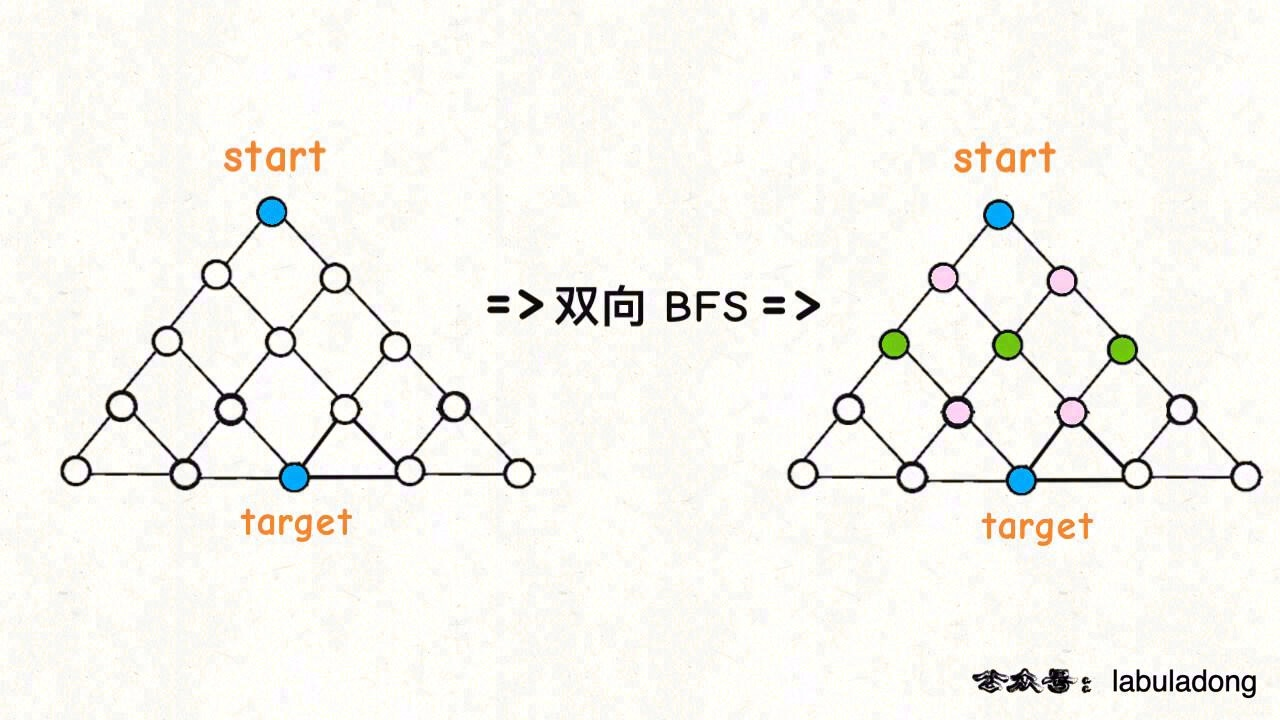
双向 BFS 还是遵循 BFS 算法框架的,只是不再使用队列,而是使用 HashSet 方便快速判断两个集合是否有交集。
另外的一个技巧点就是 while 循环的最后交换 q1 和 q2 的内容,所以只要默认扩散 q1 就相当于轮流扩散 q1 和 q2。
其实双向 BFS 还有一个优化,就是在 while 循环开始时做一个判断:
因为按照 BFS 的逻辑,队列(集合)中的元素越多,扩散之后新的队列(集合)中的元素就越多;在双向 BFS 算法中,如果我们每次都选择一个较小的集合进行扩散,那么占用的空间增长速度就会慢一些,效率就会高一些。
拓扑排序:
利用度,从下往上遍历,从叶子节点往根遍历。(以树为例子)
普通 bfs , 从根往叶子节点遍历,找最短树深度(以树为例)
class Solution { public: vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) { if (n ==1) return vector<int>(1,0); vector<int> degree(n,0); vector<vector<int>> tree(n); for(int i = 0; i < edges.size();i++) { degree[edges[i][0]]++; degree[edges[i][1]]++; tree[edges[i][0]].emplace_back(edges[i][1]); tree[edges[i][1]].emplace_back(edges[i][0]); } vector<int> res; queue<int> q; for(int i = 0; i < n;i++) { if (degree[i]==1) { q.push(i); } } while(!q.empty()) { int size = q.size();// bfs 需要记录层数,然后返回最后一层的结果 res.clear(); for(int i = 0;i < size; i++) { int top = q.front(); q.pop(); res.emplace_back(top); for (int edge:tree[top]) { degree[edge]--; if (degree[edge] == 1) { q.push(edge); } } } } return res; } };
111. Minimum Depth of Binary Tree (最小树深度\bfs)
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int minDepth(TreeNode* root) { if (root== nullptr) return 0; queue<TreeNode*> q; int res = 1; q.push(root); while(!q.empty()) { int sz = q.size(); for(int i = 0;i < sz;i++) { TreeNode* cur = q.front();q.pop(); // 遍历邻居 if (cur->left) q.push(cur->left); if (cur->right) q.push(cur->right); if (cur->left == nullptr && cur->right == nullptr) return res; } res++; } return res; } };
127. Word Ladder(单词变换 bfs/双向 bfs)





