887. 鸡蛋掉落

 

给你 k 枚相同的鸡蛋，并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。

已知存在楼层 f ，满足 0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都会碎，从 f 楼层或比它低的楼层落下的鸡蛋都不会破。

每次操作，你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。

请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少？

 

示例 1：

输入：k = 1, n = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，肯定能得出 f = 0 。 
否则，鸡蛋从 2 楼掉落。如果它碎了，肯定能得出 f = 1 。 
如果它没碎，那么肯定能得出 f = 2 。 
因此，在最坏的情况下我们需要移动 2 次以确定 f 是多少。 

示例 2：

输入：k = 2, n = 6
输出：3

示例 3：

输入：k = 3, n = 14
输出：4




暴力

class Solution {
public:
    int dfs(int k, int n) {
        if (k==1) return n;
        if (n == 0 || n == 1) return n;
        int res = INT_MAX;
        for (int i = 1; i < n;i++) {
                        // 碎了 or 没碎
            int t_maxa= max(dfs(k-1,i-1),dfs(k,n-i));
            res = min(res, 1 + t_max);
        }
        return res;
    }
    int superEggDrop(int k, int n) {
        return dfs(k,n);
    }
};

 

 

暴力+mome

class Solution {
public:
    int dfs(int k, int n, vector<vector<int>>& dp) {
        if (k==1) return n;
        if (n == 0 || n == 1) return n;
        if (dp[k][n]!=-1) return dp[k][n];
        int res = INT_MAX;
        for (int i = 1; i < n;i++) {
                        // 碎了 or 没碎
            int t_max= max(dfs(k-1,i-1,dp),dfs(k,n-i,dp));
            res = min(res, 1 + t_max);
        }
        dp[k][n] = res;
        return res;
    }
    int superEggDrop(int k, int n) {
        vector<vector<int>>dp (k+1,vector<int>(n+1,-1));
        return dfs(k,n,dp);
    }
};

 

 

 

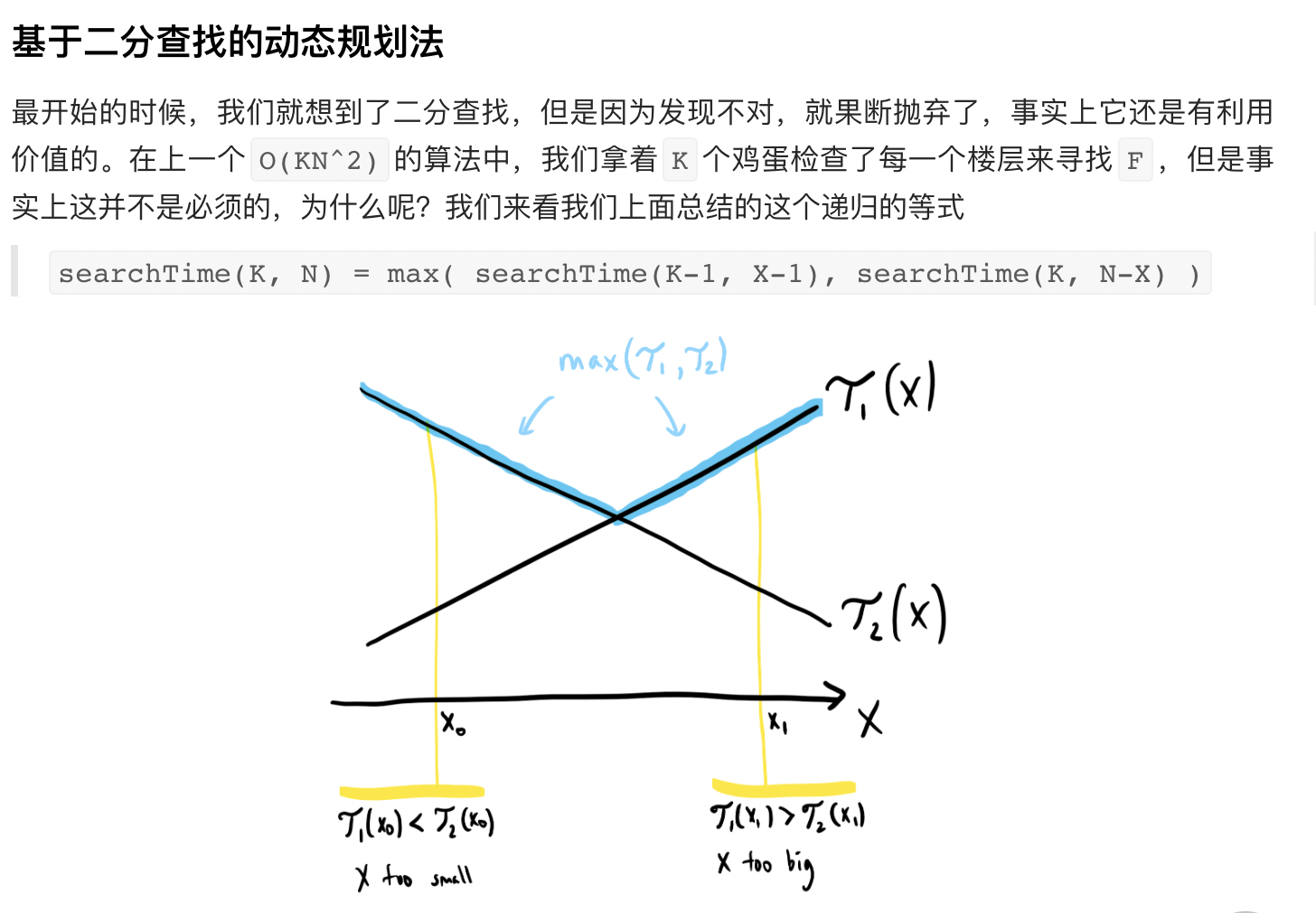
class Solution {
public:
    int dfs(int k, int n, vector<vector<int>>& dp) {
        if (k==1) return n;
        if (n == 0 || n == 1) return n;
        if (dp[k][n]!=-1) return dp[k][n];
        int res = INT_MAX;
        int low = 1,high = n;
        while(low<high) {
            int mid =  low + (high -low)/2;
            int ll = dfs(k-1,mid-1,dp);
            int rr = dfs(k,n-mid,dp);
            if (ll<rr) {
                low = mid  + 1;
            } else if (ll>rr) {
                high = mid;
            } else {
                low = high = mid;
                break;
            }
        }    
        int t_max= max(dfs(k-1,low-1,dp),dfs(k,n-low,dp));
        res = min(res, 1 + t_max);

        dp[k][n] = res;
        return res;
    }
    int superEggDrop(int k, int n) {
        vector<vector<int>>dp (k+1,vector<int>(n+1,-1));
        return dfs(k,n,dp);
    }
};

 

class Solution {
public:
    int superEggDrop(int k, int n) {
        vector<vector<int>> dp(n+1,vector<int>(k+1,0));
        for(int i = 1; i <= n;i++) {
            dp[i][1] = i;
        }
        for(int j = 1;j <= k ;j++) {
            dp[1][j] = 1;
        }
        for (int i = 2;i <= n;i++) {
            for(int j =2;j <=k;j++) {
                
                /*
                int res = INT_MAX;
                for(int t = 2;t <=i;t++) {
                // broken or not broken
                res = min(res,max(dp[t-1][j-1],dp[i-t][j])+1);
                }
                */
                int res = INT_MAX-1;
                int low = 2;
                int high = i;
                while(low<=high) {
                    int mid = low + (high - low) /2;
                    if (dp[mid-1][j-1]>dp[i-mid][j]) {
                        high = mid-1;
                    } else if(dp[mid-1][j-1]<dp[i-mid][j]){
                        low = mid+1;
                    } else {
                        low=high=mid;// = min(res,max(dp[mid-1][j-1],dp[i-mid][j])+1);
                        break;
                        }
                    //res = min(res,max(dp[mid-1][j-1],dp[i-mid][j])+1);
                }
                res = max(dp[low-1][j-1],dp[i-low][j])+1;
                
                
            dp[i][j] = res;
            }
        }
        return dp[n][k];
    }
};

 

 

 

 

 

 

 

超时https://www.bilibili.com/video/BV1KE41137PK

class Solution {
public:
    int superEggDrop(int k, int n) {
        vector<vector<int>> dp(n+1,vector<int>(k+1,0));
        for(int i = 1; i <= n;i++) {
            dp[i][1] = i;
        }
        for(int j = 1;j <= k ;j++) {
            dp[1][j] = 1;
        }
        for (int i = 2;i <= n;i++) {
            for(int j =2;j <=k;j++) {
                int res = INT_MAX;
                for(int t = 1;t <=i;t++) {
                // broken or not broken
                res = min(res,max(dp[t-1][j-1],dp[i-t][j])+1);
                }
            dp[i][j] = res;
            }
        }
        return dp[n][k];
    }
};