392. 判断子序列(双指针\dp)

难度简单507

 

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, ... , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

致谢：

特别感谢 @pbrother 添加此问题并且创建所有测试用例。

 

示例 1：

输入：s = "abc", t = "ahbgdc"
输出：true

示例 2：

输入：s = "axc", t = "ahbgdc"
输出：false

 

提示：

• 0 <= s.length <= 100
• 0 <= t.length <= 10^4
• 两个字符串都只由小写字符组成。

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int i = 0;
        int j = 0;
        while(i < s.size() && j < t.size()) {
            if(s[i]==t[j]) {
                i++;j++;
            } else {
                j++;
            }
        }
        return  i == s.size();
    }
};

 

 

 

dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

 

 

 

 

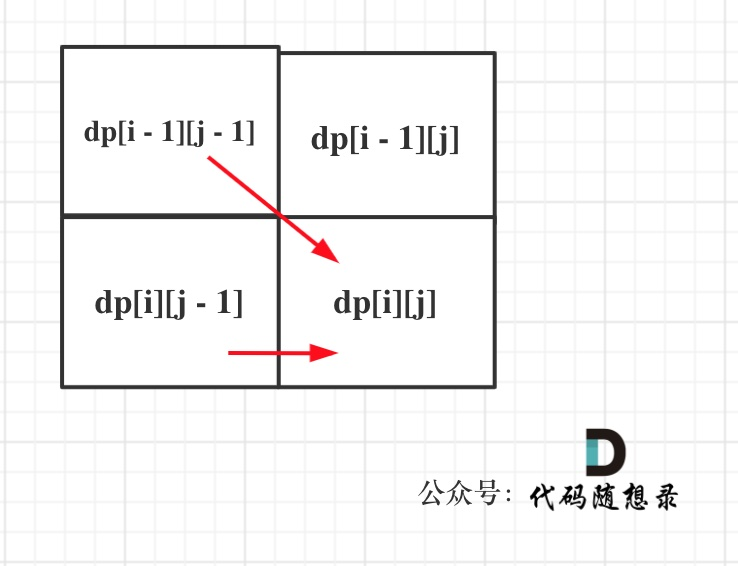
class Solution {
public:
    bool isSubsequence(string word1, string word2) {
        int n1 = word1.size();
        int n2 = word2.size();
        vector<vector<int>> dp = vector<vector<int>>(n1+1,vector<int>(n2+1,0));
        for(int i = 1; i <= n1 ;i++){
            for(int j = 1; j <= n2; j++) {
                if(word1[i-1]==word2[j-1]) {
                    dp[i][j] = 1 + dp[i-1][j-1]; 
                } else {
                    dp[i][j] = dp[i][j-1];
                }
            }
        }
        return dp[n1][n2]==n1;
    }
};

 

 

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int n = s.size();
        int m = t.size();
        // s[:i] 与t[:j] 子序列长度
        int dp[n+1][m+1]; 

        for(int i = 0;i < n+1; i++) {
            dp[i][0] = 0;
        }
        for(int j = 0; j < m+1;j++) {
            dp[0][j] = 0;
        }

        for(int i =1;i<n+1;i++) {
            for(int j = 1;j < m+1;j++) {
                if(s[i-1]==t[j-1]) {
                    dp[i][j] = 1 +dp[i-1][j-1];
                } else {
                    // 删除 t[j]
                    dp[i][j] = dp[i][j-1]; 
                }
            }
        }


        return dp[n][m] == s.size();
    }
};