神经网络反向传播，通俗理解

 

 

前置知识：

sigmod 函数

g(z) = 1 / (1 + np.exp(-z))
g'(z) = (1 / (1 + np.exp(-z))) * (1 - (1 / (1 + np.exp(-z))))
g'(z) = g(z) * (1 - g(z))

 

LR-----1层神经网络

 

 

dL/dz 简称dz_，L(a,y）使用交叉熵。

 

 

 

da_ = dL/da = (-(y/a) + ((1-y)/(1-a)))

dz_ = dL/da * da/dz = da_*   g'(z)

dw_ = dL/dz *dz/dw = dz* x

db_ = dz

 

2层神经网络

 

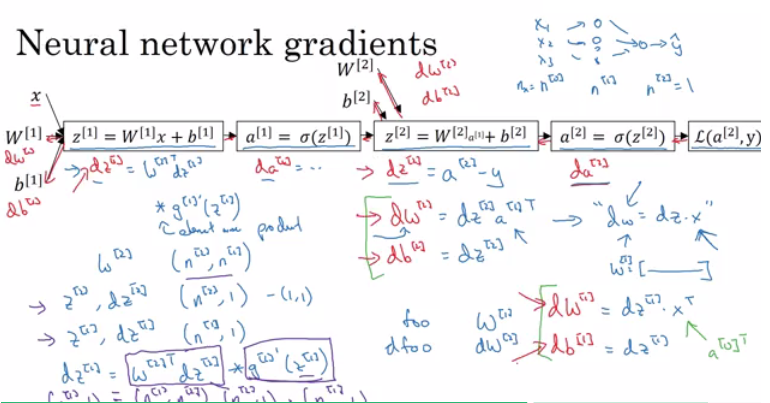
da_2 = dL/da2 =  (-(y/a) + ((1-y)/(1-a)))

dz_2 = dL/da2 * da2/dz2 = da_2*  g'(z2)

dw_2 = dL/dz2 *dz2/dw2 = dz_2* a1

db_ 2= dz_2

 

da_1 =dz_2* w2

dz_1 = dL/da1 * da2/dz1 = da_1* g'(z1)

dw_1 = dL/dz1 *dz1/dw1 = dz_1*  a0(x)

db_ 1= dz_1

 

 

多层神经网络

 

• Pseudo code for forward propagation for layer l:

  Input  A[l-1]
  Z[l] = W[l]A[l-1] + b[l]
  A[l] = g[l](Z[l])
  Output A[l], cache(Z[l])
  

• Pseudo code for back propagation for layer l:

  Input da[l], Caches
  dZ[l] = dA[l] * g'[l](Z[l])
  dW[l] = (dZ[l]A[l-1].T) / m
  db[l] = sum(dZ[l])/m                # Dont forget axis=1, keepdims=True
  dA[l-1] = w[l].T * dZ[l]            # The multiplication here are a dot product.
  Output dA[l-1], dW[l], db[l]
  

• If we have used our loss function then:

  dA[L] = (-(y/a) + ((1-y)/(1-a)))

 

https://github.com/mbadry1/DeepLearning.ai-Summary/tree/master/1-%20Neural%20Networks%20and%20Deep%20Learning#deep-l-layer-neural-network