数论-裴蜀定理-扩展欧几里得算法

裴蜀定理

对于任意的整数a、b，都存在一对整数x、y（注意x和y可以是负整数），使得\(ax+by = gcd(a,b)\)成立。或者可以这样描述：对方程\(ax+by = c，(a,b,c∈Z)\)，只有满足\(gcd(a,b)|c\)（即a和b的最大公约数可以整除c），方程才有整数解。

裴蜀定理的证明

已知\(gcd(a,b) = gcd(b,a\%b)\)，递归边界就是\(b=0，a=gcd(a,b)\)。这个时候\(ax+by = gcd(a,b)\)，只需令\(x = 1, y = 0\)，即可。

从递归边界回归的过程中，当前存在整数x'和y'满足：\(a'x' + b'y' = gcd(a,b)\)，再往上一层，则有：\(a' = b ， b' = a\%b = a - a/b*b\)，代入上式有：

\(bx' + (a-a/b*b)y' = gcd(a,b)\)，即：\(bx' + ay' - a/b*by' = ay' +b(x'-a/b*y') = gcd(a,b)\)。

根据\(ax + by = gcd(a,b)\) , 得：\(x = y'，y = (x' - a/b*y')\)。

因为\(y'\)是整数，\(x'\)也是整数，而\(a/b\)也是向下取整后的整数结果，因此，可以得知：\(x\)和\(y\)也是整数。由此可归纳得证。
以上证明方法，也称为扩展欧几里得算法。

扩展欧几里得算法模板

int exgcd(int a, int b,int &x,int &y){
  if(b==0){		    // 边界
    x = 1, y = 0 ;
    return a;
  }
  int d = exgcd(b,a%b,x,y);
  int k = x;                //K 为 x'
  x = y;		    //x 为 y'
  y = k - a/b*y;            //y 为 x' - a/b*y'
  return d;
}

求解不定方程

对于方程\(ax+by = c, gcd(a,b)|c\) ，可以调用\(exgcd(a,b,x,y)\)，计算出方程\(ax+by = gcd(a,b)\)的一组特解\((x_0,y_0)\)

设 \(d=c/gcd(a,b)\)，则\(ax_0*d+by_0*d=gcd(a,b)*d=c\)，故\((x_0*d,y_0*d)\)是方程\(ax+by = c\) 的一组解

求不定方程\(ax+by = c\) 的任意一组解\((x,y)\) ,则有 \(ax + by = c\)与 \(ax' + by' =c\) 相减得 \(a(x−x') = b(y'-y)\)

得到\(\dfrac{a}{gcd(a, b)}(x−x') = \dfrac{b}{gcd(a, b)}(y'−y)\)

因为\(gcd(\dfrac{a}{gcd(a, b)},\dfrac{b}{gcd(a, b)})=1\)，所以\(\dfrac{a}{gcd(a, b)}|y' − y\)。

故存在整数t，使得 \(y'-y =\dfrac{a}{gcd(a, b)}t\)，即 \(y = y'−\dfrac{a}{gcd(a, b)}t\)，同理有 \(x = x'+\dfrac{b}{gcd(a, b)}t\)

由 x, y 的任意性，方程的全部解都可以表示为 \((x'+\dfrac{b}{gcd(a, b)}t，y'−\dfrac{a}{gcd(a, b)}t)\) , 其中\((x',y')\)由\((x_0*d,y_0*d)\)得来，\(t∈Z\)。

求x的最小正整数解，设\(P=\dfrac{b}{gcd(a, b)}\)，那么

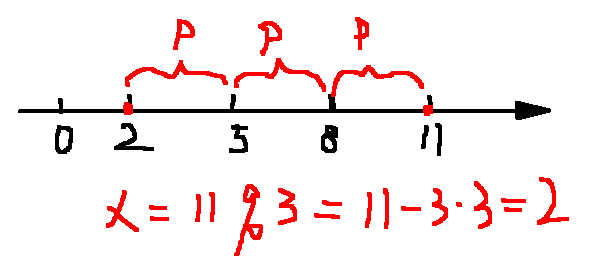
当\(x'>0\)时，则\(x=x'\%P\)，相当于\(t\)为负整数，让\(x'\)减少\(t\)倍\(P\)，直到最小正整数解，例如当\(x'=11，P=3,t=-3\) 时，使\(x=11-3*3=2\) , 相当于 \(x=11\%3=2\)

当\(x'< 0\)时，则\(x=(x'\%P+P)\%P\)，相当于\(t\)为正整数，让\(x'\)增加到最小正整数,例如当\(x'=-11，P=3,t=4\) 时，使\(x=-11+3*4=1\) , 相当于 \(x=(-11\%3+3)\%3=(-2+3)\%3=1\)

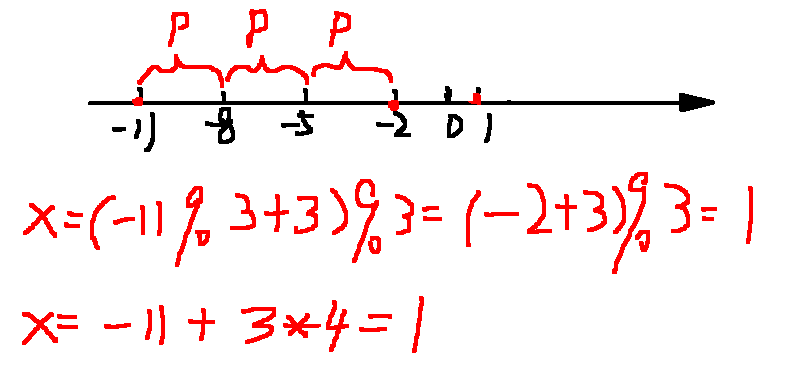
举例：青蛙约会 http://poj.org/problem?id=1061

分析：

设青蛙A和青蛙B跳跃了t次后相遇，则相对于起点0，青蛙A总路程为\(x+mt\) ,青蛙B总路程为\(y+nt\) ,满足\(x+mt=y+nt + kl\) ,\(k∈Z\)。

化解方程为\((m-n)t+kl=y-x\) , 设\(a=m-n,b=l,c=y-x\) , 则有\(at+bk=c\),本题要求t的最小正整数解，若\(gcd(a,b)\nmid c\)，则说明无解。

利用扩展欧几里得算法实现如下：

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
ll x, y, m, n, l, a, b, c, _x, _y;
ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (b == 0) {  // 边界
        x = 1, y = 0;
        return a;
    }
    ll d = exgcd(b, a % b, x, y);
    ll k = x;           // K 为 x'
    x = y;              // x 为 y'
    y = k - a / b * y;  // y 为 x' - a/b*y'
    return d;
}
int main() {
    scanf("%lld %lld %lld %lld %lld", &x, &y, &m, &n, &l);
    a = m - n, b = l, c = y - x;
    if (a < 0) {  //方便计算gcd(a,b)为正整数，a与c一起变号，k为任意整数，故不考虑k
        a = -a, c = -c;
    }
    ll _eg = exgcd(a, b, _x, _y);  //_x可能是负数
    if (c % _eg)
        puts("Impossible");
    else {
        ll d = c / _eg, p = b / _eg;
        _x = _x * d;  //_x不一定是最小正整数解
        if (_x > 0) {
            printf("%lld\n", _x % p);  //相当于_x 减去 t个p 后最小正整数解
        } else {
            printf("%lld\n", (_x % p + p) % p);  //相当于_x 加上 t个p 后最小正整数解
        }
    }
    return 0;
}