结对项目作业

结对项目作业

项目	内容
作业所属课程	2020春季计算机学院软件工程（罗杰，任健）
作业要求	结队项目作业
教学班级	005
项目地址	https://github.com/Therp-GY/Pair_intersect

PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	20	15
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	600	500
· Design Spec	· 生成设计文档	20	20
· Design Review	· 设计复审 (和同事审核设计文档)	20	30
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	20	10
· Design	· 具体设计	30	15
· Coding	· 具体编码	480	200
· Code Review	· 代码复审	60	30
· Test	· 测试（自我测试，修改代码，提交修改）	120	120
Reporting	报告
· Test Report	· 测试报告	15	10
· Size Measurement	· 计算工作量	15	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	60
	合计	1430	1020

结对编程中对接口的设计

我们在设计接口前，主要针对信息隐藏，接口设计和松耦合相关的知识进行研究并设计我们的接口。

在信息隐藏方面，我们所用到的类都是通过接口类来进行访问，对于接口类的内部数据结构和数据，我们采用private来进行私密保护，对于类的访问都是通过公开的函数实现。

在松耦合我们的目标就是降低软件模块之间的依赖程度，为此我们要以尽量少的数据交流，实现模块之间的结合。在我们的UI模块和core计算模块中，主要通过UI模块调用add_object和delete_object来传入几何对象的坐标信息，再通过get_point_gui得到交点的坐标信息进行绘制。这样模块之间调用起来较为方便，在测试上也会简化工作。

计算模块接口的设计与实现过程

计算模块中的类：

Point:

double distance(const Point& point)const;　　//　　求点与点之间距离

Line:

　　　//    线线交点
int find_intersection(const Line &line, Point *p) const; 
    //    圆线交点
int find_intersection(const Circle& circle, Point* p) const;    

Circle:

　　//　　圆线交点
int find_intersection(const Line& line , Point *p)const;
　　//　　圆圆交点
int find_intersection(const Circle& circle, Point* p)const;

关键函数比较离散，并不复杂。线线、圆线都是独立求的，圆圆会转化为圆线相交，逻辑比较简单。

算法关键：

本次结对项目引入了线段和射线

• 因此当计算线线交点和线圆交点时，所得到的点可能并不在线类（Line、Ray、Seg）上，因此需要增加判断点是否在线上的函数contain()。引入contain()后，即将求出的交点一一用contain()判定，不在线上则舍去。

　　contain（）：由于我是使用double类型并引入eps精度，因此若直接带入点，有可能出现如下情况：虽然点确实是在线上，但是由于坐标数值过大带入所　　得到的值可能超过精度值，·　　从而判定点不在直线上。因此我没有采用带入点的方法。当初始化线类时会有两个初始点start_point和end_point，我计算其方　　向向量（（end_point - start_point）/ |（end_point - 　　　start_point）|）= v并存入线类中。判断某个点是否在线上，先判断是否等于两个初始点中的一个，　　相等则在线上，若不等：

　　　　计算该点和start_point的方向向量v'

　　　　1.线为Line：若|v'| == v 则在线上。

　　　　2.线为Ray：若 v' == v 则在射线上。

　　　　3.线为Reg：若 v' == v 则在射线上且该点坐标介于start_point和end_point之间，则在线段上。

• 判断两条线有无限交点时，不能单纯靠线的a、b、c参数判定，我引入 coincide()函数

　　coincide()：线l1的两个初始点start_point1、end_point1 ，线l2的两个初始点start_point2、end_point2，则判断start_point1、end_point1是否在l2上，start_point2、end_point2是否在l1　　上，若有三个点即以上满足条件，则两条线有无数个交点。若有两个点，则判断这两个点是否为同一个点，否，则　　两条线有无数个交点。

计算模块的UML图

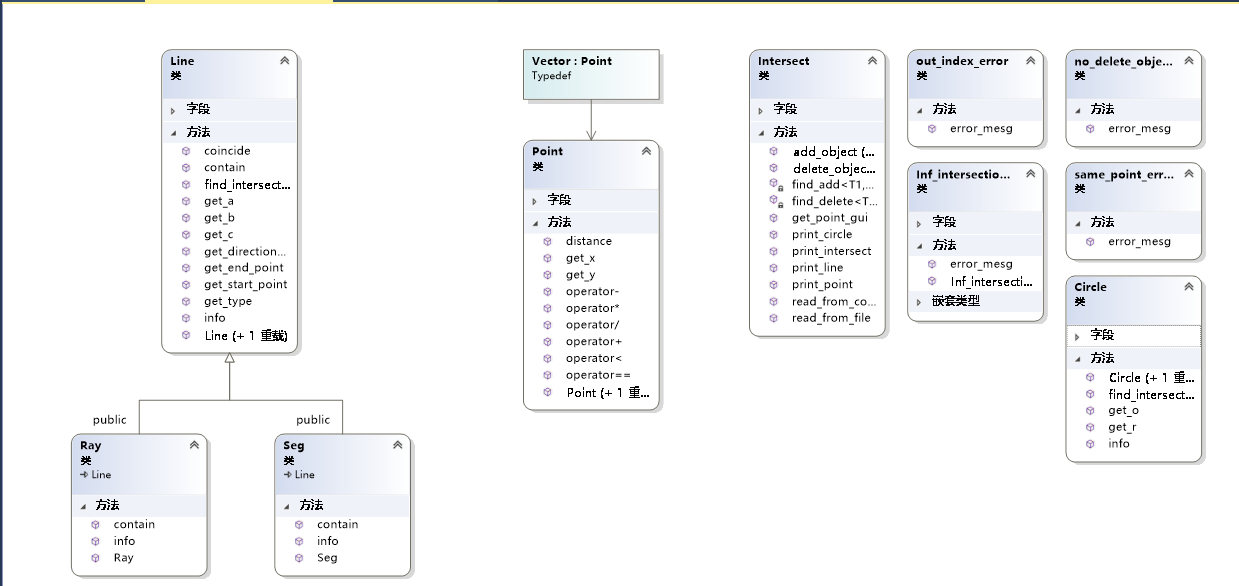
计算模块接口部分的性能改进

由于本次项目时间大部分花在接口的设计上，因此在性能上没有做出很多改进。

性能分析图：

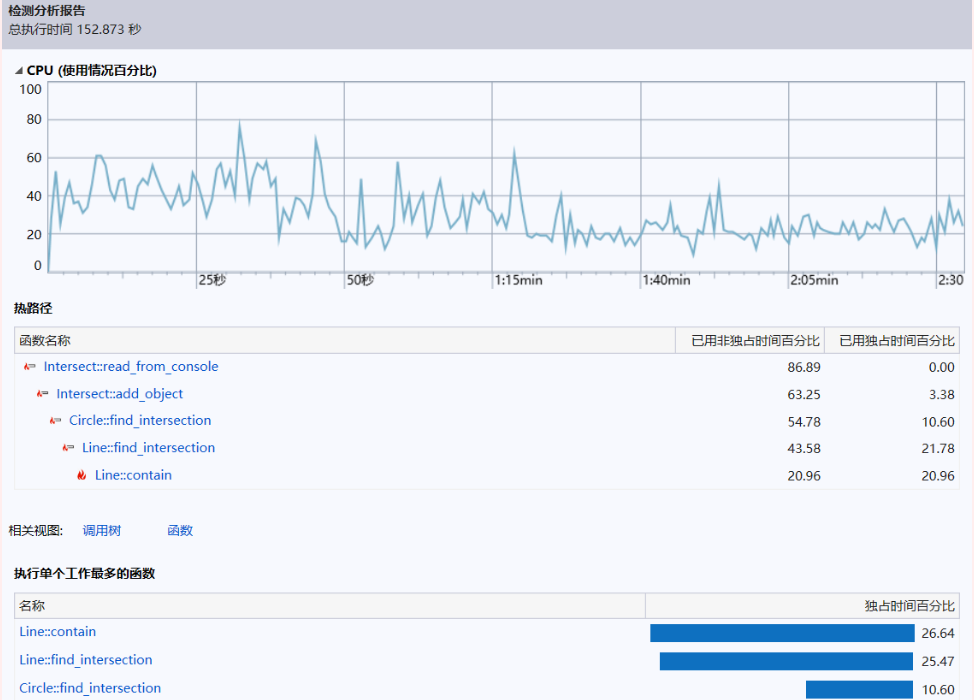
更改思路：结果得出，contain()函数是消耗时间最多的。回到程序中，我发现由于增加了Ray和Seg，我在每一次求交点（线线、圆线）时，我都需要调用contain()判断交点是否在线上，然而实际上当线类为直线时，我并不需要判定，因此我做出如下改动

更改前：

Point t0 = p[0];
        Point t1 = p[1];
        n = 0;
        if (line.contain(t0)) {
            p[n++] = t0;
        }
        if (line.contain(t1)) {
            p[n++] = t1;
        }
        return n;

更改后：

        Point t0 = p[0];
        Point t1 = p[1];
        n = 0;
        if (line.get_type() == 'L' || line.contain(t0)) { //判断是否为直线
            p[n++] = t0;
        }
        if (line.get_type() == 'L' || line.contain(t1)) {
            p[n++] = t1;
        }
        return n;

更改后性能图：

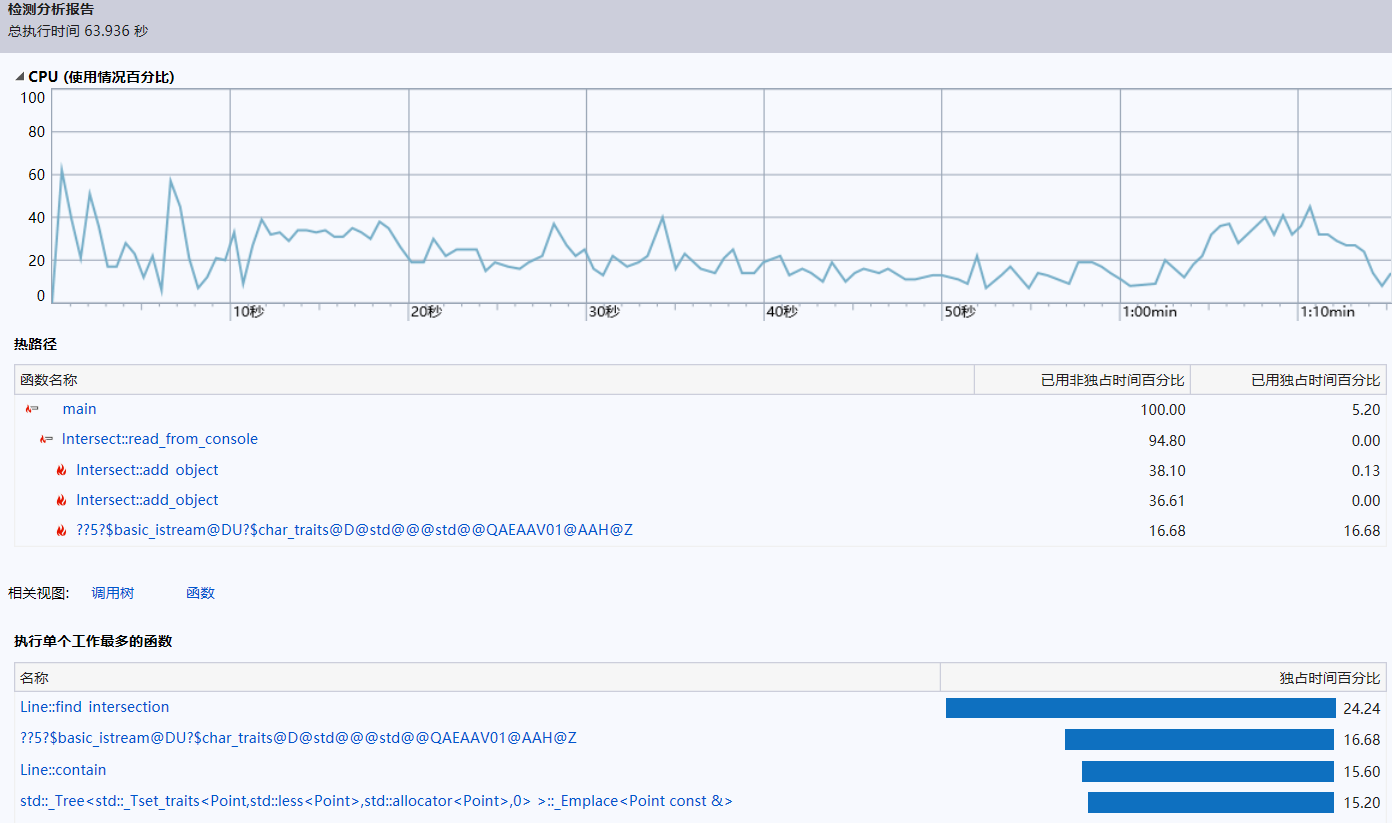
可见contain()函数所占时间百分比大大降低，性能得到提升。

*（然而当线类都为射线或者线段时，无法避免调用contain()函数，会消耗大量运行时间）

Design by Contract, Code Contract

当我们调用一个方法函数，对于要传入的参数，我们是否能够保证传入的参数符号函数的预期，我们应该如何去检查传入的参数是否符合我们的使用规范。这种种问题都是契约式设计所要解决的。

契约式设计是一种设计计算机软件的方法，它描述了一种接口规范，软件设计者可以借此对软件的组件定义更加正式，准确，并可验证。契约式设计扩展了抽象数据类型对于先验条件，后验条件和不变式的一般定义。

在本次的结对项目中，我们主要是考虑UI模块和core计算模块的组合对接，在UI模块调用core模块中计算功能的方法时，需要保证相关的参数类型，个数符合规范，以及得到的返回值数据类型加以处理利用，得到交点的坐标和个数。

优点：

使用者和调用者双方都必须履行义务，也有使用权利，保证了双方的代码质量，提高了软件工程的效率和质量；

有助于测试，帮助开发者更好理解代码；

支持复用。

缺点：

对程序语言有一定的要求，需要一种机制来验证契约的成立与否，造成代码的冗余和不可读性；

需要大量的实践。

计算模块部分单元测试展示

测试代码：

[](javascript:void(0)😉

    vector<std::pair<double, double>>  point_gui_list;
    Intersect intersect;
    const char* s = "input.txt";
    intersect.read_from_file(s);
    /*　　正常输入数据
    4
    C -3 3 3
    C -3 2 2
    S 2 4 3 2
    L -1  4  5  2
    */
    intersect.read_from_console();
    /*
    3
    C 3 3 3
    C 3 3 3    　圆重合异常
    R 3 0 5 3  
    R 5 3 7 6   线重合异常
    L 0 0 0 0   
    S 1 0 1000000 20   坐标范围异常
    C 6 7 3
    */
    intersect.print_intersect();
    intersect.delete_object('S', 2, 4, 3, 2);　　//　删除线类
    intersect.print_intersect();
    intersect.add_object('S', 2, 4, 3, 2);　　//　添加线类
    intersect.print_intersect();
    intersect.delete_object('C' ,3,  3,  3);　　//　　删除圆类
    intersect.print_intersect();
    intersect.add_object('C', 3, 3, 3);　　//　　添加圆类
    intersect.print_intersect();
    point_gui_list = intersect.get_point_gui();　　//　　得到交点坐标

    //    cout << 14
    cout << point_gui_list.size();

[](javascript:void(0)😉

测试思路：先从文件中读取数据，再从命令行读取数据（通过命令行读取时的错误数据输入覆盖异常测试），覆盖测试读取数据函数。然后增加删除几何体（线、圆），覆盖所有核心计算模块（线线交点、线圆交点、圆圆交点）。最后得到交点list，打印交点个数，和实际个数吻合

覆盖截图：

总覆盖率超过90%

计算模块部分异常处理说明

异常目标：

同端点异常 same_point_error：当输入线类时，两个端点相同，则抛出异常。

超范围异常 out_index_error：当输入数据（点坐标、圆半径）、交点坐标超过100000，抛出异常。

无限交点异常 Inf_intersection_error：当存在两个几何体的交点有无数个，抛出异常。

删除异常 no_delete_object_error：当删除一个并不存在的几何体（即输入时并没有添加的几何体），抛出异常

异常单元测试：

• same_point_error

[](javascript:void(0)😉

            int a = 0;
            try
            {
                Point a1(-1000, 0);
                Point b1(-1000, 0);
                Seg l1(a1, b1);　　//　　相同端点，应抛出异常
            }
            catch (const same_point_error s)
            {
                a = 1;
            }
            Assert::AreEqual(1, a);

[](javascript:void(0)😉

• out_index_error

[](javascript:void(0)😉

            a = 0;
            try
            {
                Circle r1(Point(-1, 200), 100002);　　//　　圆半径超过范围，应抛出异常
            }
            catch (const out_index_error o)
            {
                a = 1;
            }
            Assert::AreEqual(1, a);

[](javascript:void(0)😉

• Inf_intersection_error

[](javascript:void(0)😉

            Point p[2];
            int a = 0;
            try
            {
                Point a1(0, 0);
                Point b1(2, 2);
                Seg l1(a1, b1);

                Point a2(1, 1);
                Point b2(3, 3);
                Ray l2(a2, b2);
                l1.find_intersection(l2,p);　　//　　线段l1和射线l2有无限个交点，应抛出异常
            }
            catch (const Inf_intersection_error i)
            {
                a = 1;
            }
            Assert::AreEqual(1, a);

[](javascript:void(0)😉

• no_delete_object_error

[](javascript:void(0)😉

            Intersect intersect;
            int a = 0;
            try
            {
                Line l(Point(1, 1), Point(2, 2));
                intersect.add_object('L',1,1,2,2);
                intersect.delete_object('L', 1, 1, 2, 3);　　//　　intersect中并没有('L', 1, 1, 2, 3)这一条直线，应抛出异常
            }
            catch (const no_delete_object_error n)
            {
                a = 1;
            }
            Assert::AreEqual(1, a);

[](javascript:void(0)😉

界面模块的详细设计过程

在这次的界面模块设计中，我们采用的是QT软件，基于c++开发的UI模块。在此基础上，我们学习了一下QT的基本使用方法，以及在QT中需要用到的数据类型和方法来构建页面。最后通过设计，我们得到了一个建议的坐标轴界面，可以进行对几何对象的绘制，同时支持添加和删除几何对象，以及调用计算交点个数并绘制。

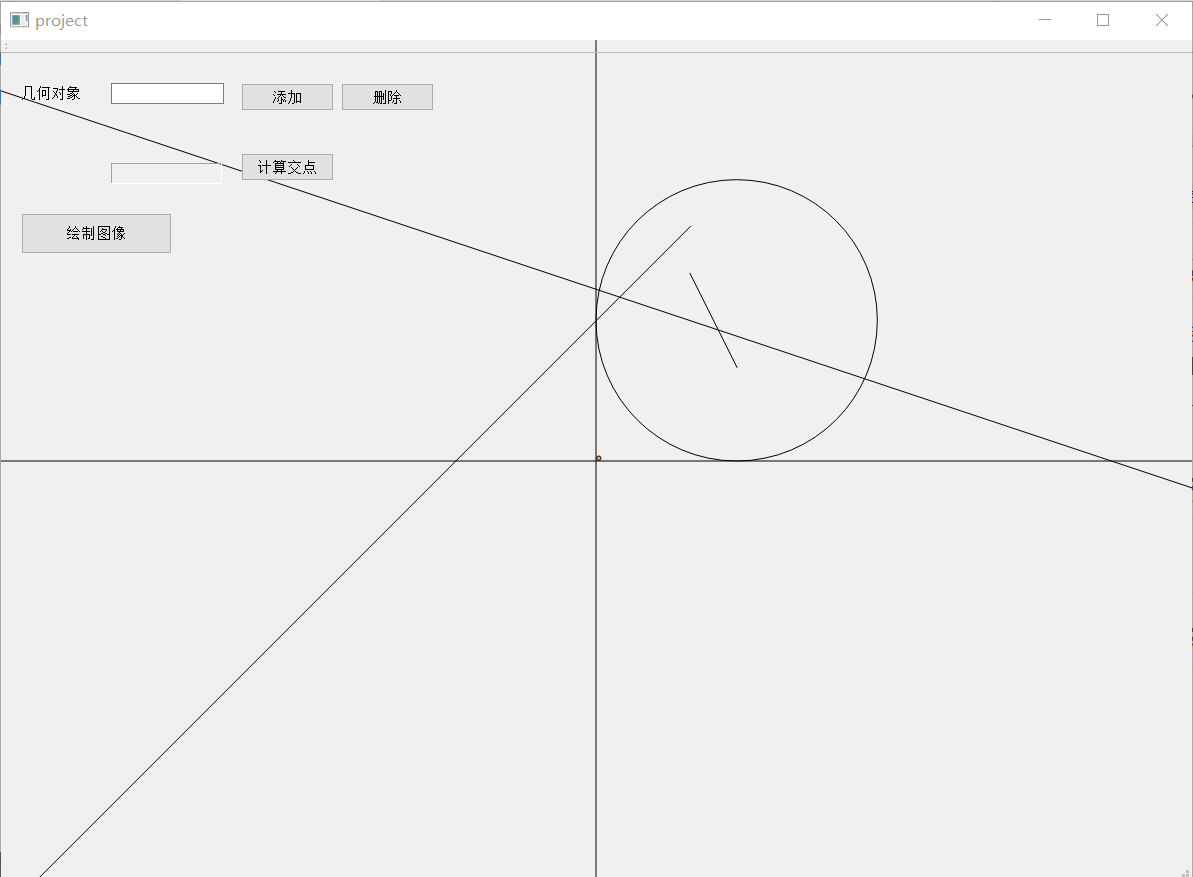
首先，模块从input.txt文件中导入几何对象的坐标信息，利用相应的数据结构储存坐标点信息

QFile file("E:/QT-GUI/UI/input.txt");
    file.open(QIODevice::ReadOnly | QIODevice::Text);
    QTextStream in(&file);
    QString line = in.readLine();
    qint16 num = line.toInt();     //几何对象个数

    while (!line.isNull()) {
        line = in.readLine();
        QList<QString> list = line.split(" ");
        if (list[0].compare("L") == 0) {
            QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
            QPoint point2 = QPoint(list[3].toInt(), list[4].toInt());
            lines_1.append(point1);
            lines_2.append(point2);
        } else if (list[0].compare("C") == 0) {
            QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
            int x = list[1].toInt();
            int y = list[2].toInt();
            int z = list[3].toInt();
            if ((abs(x) + z) > size_window) {
                size_window = (double)(abs(x) + z);
            }
            if ((abs(y) + z) > size_window) {
                size_window = (double)(abs(y) + z);
            }
            circles_1.append(point1);
            circles_2.append(list[3].toInt());
        } else if (list[0].compare("S") == 0) {
            QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
            QPoint point2 = QPoint(list[3].toInt(), list[4].toInt());
            int x1 = list[1].toInt();
            int y1 = list[2].toInt();
            int x2 = list[3].toInt();
            int y2 = list[4].toInt();
            if (abs(x1) > size_window) {
                size_window = (double)(abs(x1));
            }
            if (abs(y1) > size_window) {
                size_window = (double)(abs(y1));
            }
            if (abs(x2) > size_window) {
                size_window = (double)(abs(x2));
            }
            if (abs(y2) > size_window) {
                size_window = (double)(abs(y2));
            }
            segments_1.append(point1);
            segments_2.append(point2);
        } else if (list[0].compare("R") == 0) {
            QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
            QPoint point2 = QPoint(list[3].toInt(), list[4].toInt());
            int x1 = list[1].toInt();
            int y1 = list[2].toInt();
            int x2 = list[3].toInt();
            int y2 = list[4].toInt();
            if (abs(x1) > size_window) {
                size_window = (double)(abs(x1));
            }
            if (abs(y1) > size_window) {
                size_window = (double)(abs(y1));
            }
            if (abs(x2) > size_window) {
                size_window = (double)(abs(x2));
            }
            if (abs(y2) > size_window) {
                size_window = (double)(abs(y2));
            }
            rays_1.append(point1);
            rays_2.append(point2);
        }
    }

在窗口设计方面，首先是构建好一个建议的坐标轴系统，由于无法精确坐标轴的刻度大小范围，我们采用一个size_window参数来对几何对象的坐标大小信息记录，根据size_window参数来自动调节坐标轴的刻度大小范围。

int side = qMin(width(),height()); //创建窗口宽高参数
    QPainter painter(this);
    painter.setRenderHint(QPainter::Antialiasing,true); //开启抗锯齿
    painter.translate(width() / 2,height() / 2); //坐标系统平移变换,把原点平移到窗口中心
    painter.scale(side / (3.0 * size_window),side / (3.0 * size_window)); //坐标系统比例变换,使绘制的图形随窗口的放大而放大
    painter.scale(1,-1); //Y轴向上翻转,翻转成正常平面直角坐标系
    painter.setPen(QPen(Qt::black,height() / 2000));
    painter.drawLine(-200000,0,200000,0);
    painter.drawLine(0,150000,0,-150000);
    painter.setPen(QPen(Qt::black, height() / 2000));

在绘制部分，我们采用一些QT的QPainter中的方法，比如drawLine,drawEllipse来绘制直线，圆等几何对象，对于绘制坐标点，我们实际上也根据坐标轴刻度绘制一个以交点为中心的小圆圈以便观察。

对于添加和删除功能，我们设计了两个槽函数来对输入的坐标信息进行处理：

QString tempStr;
    QList<QString> list = ui->lineEdit_2->text().split(" ");
    if (list[0].compare("L") == 0) {
        QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
        QPoint point2 = QPoint(list[3].toInt(), list[4].toInt());
        lines_1.append(point1);
        lines_2.append(point2);
        intersect.add_object('L', list[1].toDouble(), list[2].toDouble(),
                list[3].toDouble(), list[4].toDouble());
    } else if (list[0].compare("C") == 0) {
        QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
        circles_1.append(point1);
        circles_2.append(list[3].toInt());
        intersect.add_object('C', list[1].toDouble(), list[2].toDouble(),
                list[3].toDouble());
    } else if (list[0].compare("S") == 0) {
        QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
        QPoint point2 = QPoint(list[3].toInt(), list[4].toInt());
        segments_1.append(point1);
        segments_2.append(point2);
        intersect.add_object('S', list[1].toDouble(), list[2].toDouble(),
                list[3].toDouble(), list[4].toDouble());
    } else if (list[0].compare("R") == 0) {
        QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
        QPoint point2 = QPoint(list[3].toInt(), list[4].toInt());
        rays_1.append(point1);
        rays_2.append(point2);
        intersect.add_object('R', list[1].toDouble(), list[2].toDouble(),
                list[3].toDouble(), list[4].toDouble());
    }

QList<QString> list = ui->lineEdit_2->text().split(" ");
    if (list[0].compare("L") == 0) {
        QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
        QPoint point2 = QPoint(list[3].toInt(), list[4].toInt());
        for (int i = 0; i < lines_1.length(); i++) {
            if (lines_1.at(i) == point1 && lines_2.at(i) == point2) {
                lines_1.removeAt(i);
                lines_2.removeAt(i);
                break;
            }
        }
        intersect.delete_object('L', list[1].toDouble(), list[2].toDouble(),
                list[3].toDouble(), list[4].toDouble());
    } else if (list[0].compare("C") == 0) {
        QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
        for (int i = 0; i < circles_1.length(); i++) {
            if (circles_1.at(i) == point1 && circles_2.at(i) == list[3].toInt()) {
                circles_1.removeAt(i);
                circles_2.removeAt(i);
                break;
            }
        }
        intersect.delete_object('C', list[1].toDouble(), list[2].toDouble(),
                list[3].toDouble());
    } else if (list[0].compare("S") == 0) {
        QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
        QPoint point2 = QPoint(list[3].toInt(), list[4].toInt());
        for (int i = 0; i < segments_1.length(); i++) {
            if (segments_1.at(i) == point1 && segments_2.at(i) == point2) {
                segments_1.removeAt(i);
                segments_2.removeAt(i);
                break;
            }
        }
        intersect.delete_object('S', list[1].toDouble(), list[2].toDouble(),
                list[3].toDouble(), list[4].toDouble());
    } else if (list[0].compare("R") == 0) {
        QPoint point1 = QPoint(list[1].toInt(), list[2].toInt());
        QPoint point2 = QPoint(list[3].toInt(), list[4].toInt());
        for (int i = 0; i < rays_1.length(); i++) {
            if (rays_1.at(i) == point1 && rays_2.at(i) == point2) {
                rays_1.removeAt(i);
                rays_2.removeAt(i);
                break;
            }
        }
        intersect.delete_object('R', list[1].toDouble(), list[2].toDouble(),
                list[3].toDouble(), list[4].toDouble());
    }

最后是对交点的绘制，我们通过访问core模块，得到相应的返回值后，对返回的数据结构进行相应的处理，可以得到所有交点的坐标信息。

std::vector<std::pair<double, double>> points_1 = intersect.get_point_gui();
    ui->label_2->setText(tempStr.setNum(points_1.size()));
    for (int i = 0; i < points_1.size(); i++) {
        points.append(QPointF(points_1.at(i).first, points_1.at(i).second));
    }

界面模块与计算模块的对接

我们首先将core计算模块封装为dll文件，其中还有相应的头文件和.lib文件，将其作为外部库导入到界面模块GUI中，在GUI的调用过中，通过接口类Intersect传入参数得到相应的反馈。

在实际的对接过程中，我们首先创建一个Intersect类，通过intersect导入文件的几何对象坐标描述，在此同时intersect在core中构建出几何图像的交点信息，在UI模块添加和删除几何对象时，也调用intersect相应的方法添加和删除几何体。最后，GUI如要获取交点信息，通过get_point_gui()得到一个包含所有交点信息的数据返回值。

Intersect intersect;
const char* s = "input.txt";
intersect.read_from_file(s);

intersect.add_object('S', list[1].toDouble(), list[2].toDouble(),
                list[3].toDouble(), list[4].toDouble());

intersect.delete_object('L', list[1].toDouble(), list[2].toDouble(),
                list[3].toDouble(), list[4].toDouble());

std::vector<std::pair<double, double>> points_1 = intersect.get_point_gui();
    ui->label_2->setText(tempStr.setNum(points_1.size()));
    for (int i = 0; i < points_1.size(); i++) {
        points.append(QPointF(points_1.at(i).first, points_1.at(i).second));
    }

描述结对的过程

由于此次结对编程过程条件有限，双方只能通过网络进行交流，所有稍有不便，我们主要通过微信语音交流和腾讯会议远程协作。

结对编程的优缺点

优点：

1. 提高个人的一些能力，通过相互学习提高自己的认知
2. 加强团队配合能力，在结对实践中清晰自己的不足，需要改进的地方
3. 提高自己的积极性，实现双方1+1>2
4. 提高软件项目的质量，共同解决问题

缺点：

1. 双方的了解不多，导致初次配合存在问题，可以多磨合相互促进
2. 没有合理地安排可能会导致时间的浪费
3. 有很多项目并不一定适合结队编程