本文是机器学习系列的第一篇文章, 在写这篇文章之前, 我思考了很久,该如何开始这一系列的内容..
我很久以前看过一篇ted上讲解的视频给了我启发.
本篇文章将用我认为最好理解的方式介绍机器学习的基本原理, 力求让没有任何基础的小伙伴也能够理解 在机器学习中, 我们是如何训练计算机"学习"的.
下面我们看看一个计算机视觉处理模型的最基本功能:
将上面的图片识别为"bird", 对于人脑来说非常简单. 但是对于传统的计算机程序来说, 这是非常非常困难的任务.
那么, 这幅图片到底是经过什么样的计算得到了"bird"这个单词的呢?
对于人来说, 识别过程大概如下如所示:
图片被视觉神经元感知, 经过一层又一层的神经元(乱七八糟的神经元),发生一次又一次的变化; 你可以想象一层又一层的神经元就是一个又一个的数学函数, 从上一层神经元数据加工后, 输出到下一层神经元.....
最终一组神经元在我们电脑里面打开了一个开关, "叮!!!" 的一下, 一盏灯就亮了, 突然冒出了4个字母"bird".
然后, 牛逼的科学家们, 把 图片的像素点, 人类的神经系统, 还有鸟, 分别抽象成了:$x,w,y$. 像下面的图片展示的一样:
在图片中,有上百万上千万的大量的x, w, 和少量的输出: y, 毕竟得出的结果:'bird'只是4个字母.
之后, 科学家们又假设了一个公式: $X '*' W = Y$, 在"乘以"上加上了引号, 表示这个"乘以"实际上是一系列复杂的数学运算.
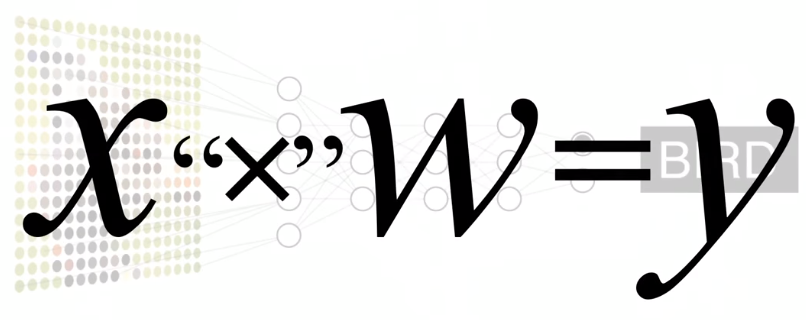
这样一个等式:$Y = X '*' W$, 只要得到其中,2个值,就能解出另外一个值, 非常简单.
我们有x, 并且我们知道y, 我们很容易就能够计算出w, 然后把w告诉计算机, 用在其它的输入:'X'上, 通过X '*' W = Y这个等式, 把Y计算出来.
但是这里的乘号'*', 是一个非常复杂的数学过程, 他可能并不存在逆运算(乘的逆运算是除), 我们不能用直接在两边同时乘以 '1/X'的方式来计算W.
那到底应该怎么计算这个W呢? 为了说明这个过程, 我们用一个更简单的栗子: 现在假设 输入值 x = 3, 输出值:y = 6
$3 * w = 6$
上面说了, 我们不能直接通过等式两边同时除以3来做这件事.
使用一种不使用除法的方式来计算, 把y移到等式左边, 随机假设一个w 的值, 然后把得到的输出值y' - 真实值y 的结果, 作为误差lossing_value, 就像下面的等式:
$3 * w - 6 = y'$
$lossing\_value = y' - y$
当这个lossing_value的值满足一定条件, 或者说, 变得非常非常小的时候, 我们说这是了一个比较有用的, 满足条件的w.
那么, 具体过程是如何做的呢?, 我们继续使用上面的栗子:
上面的栗子中, y=0, x =3, 现在随机假设一个值 w = 5, 我们看, 这个w和lossing_value其实是存在一定关系的.
$w = 5$
$3 * w - 6 = 9,\ \ \ y' - y = 9,\ \ \ lossing\ too\ large, try\ agin: w-0.5$
$w = 4.5$
$3 * w - 6 = 7.5,y' - y = 7.5,lossing\ too\ large, try\ agin: w-0.5$
$w = 4$
$3 * w - 6 = 6,\ \ \ y' - y = 6,\ \ \ lossing\ too\ large, try\ agin: w-0.5$
$......$
$w = 2$
$3 * w - 6 = 0,\ \ \ y' - y = 0,\ \ \ lossing\ small\ than\ 0.001,\ ok ,\ stop!$
以上这个过程, 就是我们训练计算机学习整个过程.
在真实的情况下, 我们需要大量的x, 以及大量的y, 我们不断的告诉计算机x, 和, y, 让计算机不停的迭代, 最终计算机可以得到一个满足条件的w, 使得lossing_value非常小.
下面说一些专业术语:
1) 每一次迭代, 调整w的值, 使得lossing_value更小. 这个过程叫: 梯度下降, 之前我们随便选择了一个w, 然后再调整, 这就是"随机梯度下降".
2) 在真实的训练中, 并不会直接使用$y' - y = lossing\_vlaue$, 毕竟 这样计算出来的$lossing\_value$可能是负值, 但是误差却更大了.
衡量误差大小有一系列专门的函数, 比如 使用方差:
$lossing\_value = \frac{\sum_{i=1}^m\sqrt{(y - y_i)^2}}{m}$
还有交叉熵..等等.
嗯...讲这里, 训练机器进行学习的最基本原理讲得就差不多了. 整个过程非常容易理解, 真实应用场景中, 也差不多是上面这个流程, 但情况会更加复杂一点.
大家不用担心, 这些内容后面有时间我也会慢慢写.
如果有条件可以看看个视频, 这篇文章很多内容就是从这个视频上来的.
抽空来完成这些文章, 对自己的学习来说是一种巩固, 但的确也会耗费不少精力. 如果大家转载文章, 请尊重作者, 注明文章来源.
如果能够您觉得文章对您有帮助, 您除了可以留言点赞之外, 还可以扫描下面的二维码, 对我进行打赏!
