上一篇文章介绍了目前大多数人在拟合手写笔迹的时候使用的算法, 这篇文章介绍一种自己独创的算法.
这种算法具有以下优点:
1) 使用二次贝塞尔曲线拟合, 计算量大概比3次贝塞尔曲线少三分之一.
2) 不必等到用户输入了下一个点之后, 才能绘制当前两个点之间的曲线, 这种算法可以先绘当前需要拟合的线段的一部分, 能够非常及时的把用户的输入反馈给用户, 用户体验立刻提高了2个档次.
3) 不用计算控制点, 处理起来更加简单, 计算量也再次减少, 用户绘制体验得到进一步提高.
4) 笔迹拟合更加接近真实手写的笔迹.
有以下缺点:
我真尼玛没发现有缺点, 我真的不能欺骗大家, 它明明没有缺点, 我非要找一个缺点出来吗!!!?,作为一个程序员, 我不能说谎啊!!!!!O(∩_∩)O哈哈~
这么厉害的算法, 大家是不是已经迫不及待了. 下面就来给大家分享这个算法的思路, 先看下面的图解:
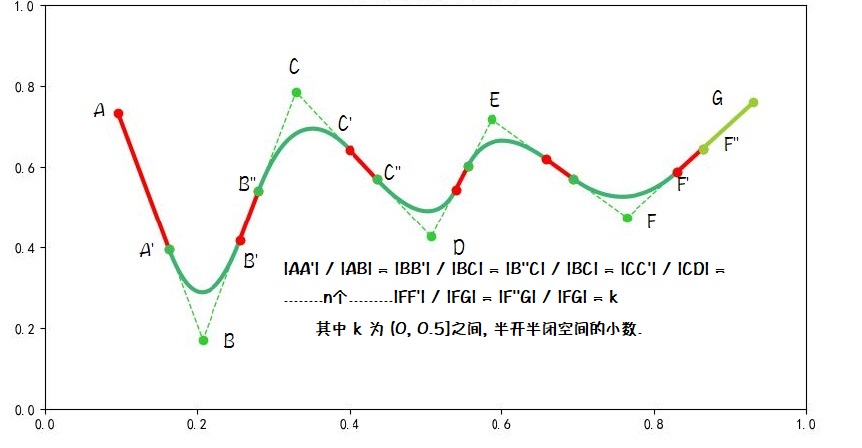
可能大家只看图就已经知道应该怎么做了. 现在按照图中的标注, 假设:ABCDEFG为原笔迹点.
1) 当用户通过点击鼠标或者点击手机屏幕手势, 输入点A时, 我们在A的位置画下一个小圆点
2) 首先需要设立一个系数k,取值为(0, 0.5]之间的小数. 当用于通过移动, 输入了第二个点B时, 我们在线段AB上找到一个点A', 使得 |A'B| / |AB| = k, 并绘制线段AA', 将其作为手写笔迹的一部分.
3) 当用户再次移动鼠标, 得到得到第三个点C时, 我们在BC上, 找到两个点, B' 和 B'', 满足 |BB'| / |BC| = |B''C| / |BC| = k, 然后将前面的 A' 和 B' 作为两个端点,
点B作为控制点, 绘制A'BB' 描述的二次贝塞尔曲线. 作为手写笔迹的一部分.
4) 连接B'B''的直线线段, 作为时候写笔迹的一部分.
5) 当用于输入点D,E,F.......时, 回到第2步, 循环执行2,3,4.
6) 当用于输入最后一个点G时, 执行2, 3步, 然后直接连接F'G, 结束绘制.
为什么要把第4步单独分离出来呢, 因为当k取值为0.5的时候, B'B'', C'C''.....F'F'' 直接重合为同一个点, 就可以直接省略弟4步.(实践证明, k值取0.5, 不但速度快, 效果还非常好!!!!)
这个算法, 初看起来, 有一些问题, 整个曲线没有经过作为原笔迹点的BCDEF, 是不是效果不理想呢???..再细想一下:
使用点ABC来举例, 虽然没有经过点B, AA'和B'B两条线段的轨迹是完全和原笔迹的连线重合的, 即使阈值取0.5的情况, 也有两个点(A', B')和原笔迹连线重合'
所以, 我们虽然放弃了一棵树,得到了一片森林;放弃一个点, 重合了无数个点, 我们还可以通过阈值k来控制曲线的拟合程度, k越小, 转角的地方越锐利; k越大, 拟合越平滑.
同样,为了大家学习方便, 我在前面一篇文章的基础上稍作修改, 把这种算法用Python实现出来, 提供大家参考和理解:
1 #!/usr/bin/env python 2 # -*- coding: utf-8 -*- 3 import numpy as np 4 from scipy.special import comb, perm 5 import matplotlib.pyplot as plt 6 7 plt.rcParams['font.sans-serif'] = ['SimHei'] 8 # plt.rcParams['font.sans-serif'] = ['STXIHEI'] 9 plt.rcParams['axes.unicode_minus'] = False 10 11 class Handwriting: 12 def __init__(self, line): 13 self.line = line 14 self.index_02 = None # 保存拖动的这个点的索引 15 self.press = None # 状态标识,1为按下,None为没按下 16 self.pick = None # 状态标识,1为选中点并按下,None为没选中 17 self.motion = None # 状态标识,1为进入拖动,None为不拖动 18 self.xs = list() # 保存点的x坐标 19 self.ys = list() # 保存点的y坐标 20 self.cidpress = line.figure.canvas.mpl_connect('button_press_event', self.on_press) # 鼠标按下事件 21 self.cidrelease = line.figure.canvas.mpl_connect('button_release_event', self.on_release) # 鼠标放开事件 22 self.cidmotion = line.figure.canvas.mpl_connect('motion_notify_event', self.on_motion) # 鼠标拖动事件 23 self.cidpick = line.figure.canvas.mpl_connect('pick_event', self.on_picker) # 鼠标选中事件 24 self.ctl_point_1 = None 25 26 def on_press(self, event): # 鼠标按下调用 27 if event.inaxes != self.line.axes: return 28 self.press = 1 29 30 def on_motion(self, event): # 鼠标拖动调用 31 if event.inaxes != self.line.axes: return 32 if self.press is None: return 33 if self.pick is None: return 34 if self.motion is None: # 整个if获取鼠标选中的点是哪个点 35 self.motion = 1 36 x = self.xs 37 xdata = event.xdata 38 ydata = event.ydata 39 index_01 = 0 40 for i in x: 41 if abs(i - xdata) < 0.02: # 0.02 为点的半径 42 if abs(self.ys[index_01] - ydata) < 0.02: break 43 index_01 = index_01 + 1 44 self.index_02 = index_01 45 if self.index_02 is None: return 46 self.xs[self.index_02] = event.xdata # 鼠标的坐标覆盖选中的点的坐标 47 self.ys[self.index_02] = event.ydata 48 self.draw_01() 49 50 def on_release(self, event): # 鼠标按下调用 51 if event.inaxes != self.line.axes: return 52 if self.pick is None: # 如果不是选中点,那就添加点 53 self.xs.append(event.xdata) 54 self.ys.append(event.ydata) 55 if self.pick == 1 and self.motion != 1: # 如果是选中点,但不是拖动点,那就降阶 56 x = self.xs 57 xdata = event.xdata 58 ydata = event.ydata 59 index_01 = 0 60 for i in x: 61 if abs(i - xdata) < 0.02: 62 if abs(self.ys[index_01] - ydata) < 0.02: break 63 index_01 = index_01 + 1 64 self.xs.pop(index_01) 65 self.ys.pop(index_01) 66 self.draw_01() 67 self.pick = None # 所有状态恢复,鼠标按下到稀放为一个周期 68 self.motion = None 69 self.press = None 70 self.index_02 = None 71 72 def on_picker(self, event): # 选中调用 73 self.pick = 1 74 75 def draw_01(self): # 绘图 76 self.line.clear() # 不清除的话会保留原有的图 77 self.line.set_title('Bezier曲线拟合手写笔迹') 78 self.line.axis([0, 1, 0, 1]) # x和y范围0到1 79 # self.bezier(self.xs, self.ys) # Bezier曲线 80 self.all_curve(self.xs, self.ys) 81 self.line.scatter(self.xs, self.ys, color='b', s=20, marker="o", picker=5) # 画点 82 # self.line.plot(self.xs, self.ys, color='black', lw=0.5) # 画线 83 self.line.figure.canvas.draw() # 重构子图 84 85 # def list_minus(self, a, b): 86 # list(map(lambda x, y: x - y, middle, begin)) 87 88 def controls(self, k, begin, end): 89 if k <= 0 or k >= 1: return 90 first_middle = begin + k * (end - begin) 91 second_middle = begin + (1 - k) * (end - begin) 92 return first_middle, second_middle 93 94 95 def all_curve(self, xs, ys): 96 le = len(xs) 97 if le < 2: return 98 self.ctl_point_1 = None 99 100 begin = [xs[0], ys[0]] 101 end = [xs[1], ys[1]] 102 self.one_curve(begin, end) 103 104 for i in range(2, le): 105 begin = end 106 end = [xs[i], ys[i]] 107 self.one_curve(begin, end) 108 109 end = [xs[le - 1], ys[le - 1]] 110 x = [self.ctl_point_1[0], end[0]] 111 y = [self.ctl_point_1[1], end[1]] 112 113 #linestyle='dashed', 114 self.line.plot(x, y, color='yellowgreen', marker='o', lw=3) 115 116 def one_curve(self, begin, end): 117 ctl_point1 = self.ctl_point_1 118 119 begin = np.array(begin) 120 end = np.array(end) 121 122 ctl_point2, self.ctl_point_1 = self.controls(0.4, begin, end) 123 color = 'red'; 124 if ctl_point1 is None : 125 xs = [begin[0], self.ctl_point_1[0]] 126 ys = [begin[1], self.ctl_point_1[1]] 127 self.line.plot(xs, ys, color=color, marker='o', linewidth='3') 128 else : 129 xs = [ctl_point1[0], begin[0], ctl_point2[0]] 130 ys = [ctl_point1[1], begin[1], ctl_point2[1]] 131 self.bezier(xs, ys) 132 xs = [ctl_point2[0], self.ctl_point_1[0]] 133 ys = [ctl_point2[1], self.ctl_point_1[1]] 134 self.line.plot(xs, ys, color=color, marker='o', linewidth='3') 135 136 def bezier(self, *args): # Bezier曲线公式转换,获取x和y 137 t = np.linspace(0, 1) # t 范围0到1 138 le = len(args[0]) - 1 139 140 self.line.plot(args[0], args[1], marker='o', linestyle='dashed', color='limegreen', lw=1) 141 le_1 = 0 142 b_x, b_y = 0, 0 143 for x in args[0]: 144 b_x = b_x + x * (t ** le_1) * ((1 - t) ** le) * comb(len(args[0]) - 1, le_1) # comb 组合,perm 排列 145 le = le - 1 146 le_1 = le_1 + 1 147 148 le = len(args[0]) - 1 149 le_1 = 0 150 for y in args[1]: 151 b_y = b_y + y * (t ** le_1) * ((1 - t) ** le) * comb(len(args[0]) - 1, le_1) 152 le = le - 1 153 le_1 = le_1 + 1 154 155 color = "mediumseagreen" 156 if len(args) > 2: color = args[2] 157 self.line.plot(b_x, b_y, color=color, linewidth='3') 158 159 fig = plt.figure(2, figsize=(12, 6)) 160 ax = fig.add_subplot(111) # 一行一列第一个子图 161 ax.set_title('手写笔迹贝赛尔曲线, 计算控制点图解') 162 163 handwriting = Handwriting(ax) 164 plt.xlabel('X') 165 plt.ylabel('Y') 166 167 # begin = np.array([20, 6]) 168 # middle = np.array([30, 40]) 169 # end = np.array([35, 4]) 170 # handwriting.one_curve(begin, middle, end) 171 # myBezier.controls(0.2, begin, middle, end) 172 plt.show()
下一篇文章,不出意外应该是这个手写笔迹系列的最后一篇文章.
我将把我实现笔锋效果的具体原理和细节, 还有用C++对算法的具体实现, 以及可以直接运行查看效果的Demo一起分享给大家.
无良公司老板拖欠两个月工资了, 穷得叮当响, .真尼玛坑啊,我靠!!!!!!!!现在每天吃8块钱的蛋炒饭, 早上点一份,中午吃一半, 晚上吃一半, 日子真实苦啊..
大家如果大家觉得这篇文章对您有帮助, 又愿意打赏一些银两, 请拿起你的手机, 打开你的微信, 扫一扫下方二维码, 作为一个有骨气的程序员攻城狮, 我非常愿意接受大家的支助...哈哈哈!!!




