从 $n$ 个人中取出 $m$ 个人，如果取出来的顺序不同就是不同的结果的话，选第一个人时有种选择，
选第二个人时, 对于前面$ n $种选择, 每一种, 都有 $n - 1$ 种选择，。。。最后一个人有 $n - m + 1$ 种选择.
所以排列的数量有:

$P_n^m = n(n-1)(n-2)...(n-m+1)$

组合

假设从 $n$ 个人中取出 $m$ 个人, 有 $C_n^m$ 种方法, 对于每一种取法, 对取出的 $m$ 个人进行排序, 其总和等于$P_n^m$,所以下面的等式成立:

$\begin{aligned} C_n^m * m! &= P_n^m => \\ C_n^m &= \frac{P_n^m}{m!}\end{aligned}$

二项式分布

二项式分布概念

假设下面的情况:

老王是条单身狗的屌丝程序员, 想着怎么找一个妹子, 老王想了一个大面积撒网,小面积培养的办法:遇到一个妹子, 就去跟她表白;
老王觉得自己还挺有魅力, 所以他假设自己每表白4次就会成功1次,
所以每次表白成功的概率为$p=0.25; $则表白失败的概率为 $q=1-p=0.75$
老王现在想算一下,如果自己对100个妹子表白, 被其中10个妹子看中的概率是多少呢?

对于100次都表白, 我们每次都用$x$来表示表白的结果:

\[\underbrace{x,x,\cdots,x}_{100} \]

这个$x$有可能是 $p$ 的概率(成功), 也可能是$1-p$(失败), 由于有10次成功, 我们可以把这10次成功随机的放到100个$x$的位置上.

一共有多少种放法?这是一个组合, 即:$C_{100}^{10}$,而基于出现在$C_{100}^{10}$中的每一种情况, 其出现的概率都是$p^{10}(q)^{90}$,只是p和q出现的顺序不一样而已.

所以, 可以得出如果老王对100个女孩表白, 成功10次的概率是:

\[C_{100}^{10}p^{10}(1-p)^{90} \]

概率质量函数(probability mass function)

根据上面的结果可以得出一个普遍的公式, 对于是n个独立的成功/失败试验中成功的次数的离散概率分布，

其中每次试验的成功概率为p,失败的概率为1-p, 则实验n次成功k次的概率为一个函数记为:

\[f(k, n, p) = C_n^mp^k(1-p)^{n-k} \]

这个$f(k,n,p)$函数称为:'概率质量函数',用于计算对于概率为p的随机事件(伯努利实验), 重复试验n次, 出现k次的概率

在wolfram上可以看到表白这件事的概率分布如下图:

累积分布函数(Cumulative Distribution Function)

老王作为一条单身汪, 也不是没有原因的, 想着想着, 竟然开始研究概率问题了:

老王想知道我要是表白100次,成功10次到15次的概率是多少呢?

所以老王把自己成功10次, 11次, 12..15次的概率加起来,得出下面的函数:

\[F(K, n, p) = \sum_{k=10}^{15}{C_n^mp^k(1-p)^{n-k}}\qquad(p=0.25, n=100) \]

$F(K,n,p)$函数就是老王表白成功的累积分布函数如图:
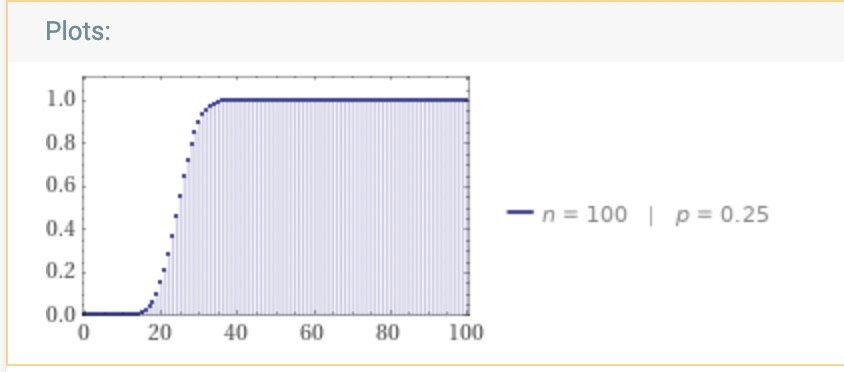
累积分布函数图形

老王表白是一个离散的事件, 在连续的情况下, 累积分布函数应该是取积分:

\[F(K, n, p) = \int\nolimits_{10}^{15}{C_n^mp^k(1-p)^{n-k}}\qquad(p=0.25, n=100) \]

泊松分布

老王每天没事就在路边对着女性表白,骚扰女性!常在路边走哪有不湿鞋, 出来混迟早要还的!!!
突然有一天老王就被一道闪电劈中了, 但是, 老王因祸得福, 居然拥有了闪电的速度, 他变成了闪电侠!
所以老王的速度越来越快, 他的每天表白的次数n可以接近无限,每天可以成功的次数变成了 $\lambda$,

所以这个时候,老王表白成功的概率可以算成$P=\frac{\lambda}{n}$, 然后我们就可以推算出泊松分布的公式了, 如下:

$\begin{aligned} f(k, n, p) &= C_n^kp^k(1-p)^{n-k} \\ &=\frac{{n(n-1)...(n-k+1)}}{k!}p^k(1-p)^{n-k} \\ &=\frac{{n(n-1)...(n-k+1)}}{k!}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k} \\ &=\frac{{n(n-1)...(n-k+1)}}{n^k}\frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n-k} \\ &=\begin{cases}\lim\limits_{n \to \infty}\frac{{n(n-1)...(n-k+1)}}{n^k}\end{cases}\frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n-k} \\ &=\begin{cases}\lim\limits_{n \to \infty}\frac{\overbrace{n(n-1)...(n-k+1)}^{k个}}{\underbrace{n * n ... * n}_{k个}}\end{cases}\frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n-k} \\ &= 1*\frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n-k} \\ &= \frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n}\begin{cases}\lim\limits_{n \to \infty}(1-\frac{\lambda}{n})^{-k}\end{cases} \\ &= \frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n}*1 \\ &= \frac{\lambda^k}{k!}\begin{cases}\lim\limits_{n\to \infty}(1+\frac{-\lambda}{n})^{n}\end{cases} \\ &= \frac{\lambda^k}{k!}e^{-\lambda} \end{aligned}$

至于最后一步推导$\begin{cases}\lim\limits_{n \to \infty}(1 - \frac{\lambda}{n}) = e^{-\lambda}\end{cases}$的证明,请看这里

所以, 当二项式分布测试样本n非常大的时候, 就可以逼近泊松分布了.

Filcoin中出块权的计算

有了上面的基础, 就可以更加深入, 开始研究Filcoin出块权的计算的原理了.

Filcoin计算出块wincount的代码如下, 后面会分几个部分进行详细的讨论:

// ComputeWinCount uses VRFProof to compute number of wins
// The algorithm is based on Algorand's Sortition with Binomial distribution
// replaced by Poisson distribution.
func (ep *ElectionProof) ComputeWinCount(power BigInt, totalPower BigInt) int64 {
	h := blake2b.Sum256(ep.VRFProof)
	lhs := BigFromBytes(h[:]).Int // 256bits, assume Q.256 so [0, 1)
	// We are calculating upside-down CDF of Poisson distribution with
	// rate λ=power*E/totalPower
	// Steps:
	//  1. calculate λ=power*E/totalPower
	//  2. calculate elam = exp(-λ)
	//  3. Check how many times we win:
	//    j = 0
	//    pmf = elam
	//    rhs = 1 - pmf
	//    for h(vrf) < rhs: j++; pmf = pmf * lam / j; rhs = rhs - pmf
	lam := lambda(power.Int, totalPower.Int) // Q.256
	p, rhs := newPoiss(lam)
	var j int64
	for lhs.Cmp(rhs) < 0 && j < MaxWinCount {
		rhs = p.next()
		j++
	}
	return j
}

关于计算$\lambda$的解释

矿工出块的概率理论受自身算力的影响和全网算力的影响,在Filcoin出块权限计算的时候, 这个$\lambda$的计算方法为:

// computes lambda in Q.256
func lambda(power, totalPower *big.Int) *big.Int {
	lam := new(big.Int).Mul(power, blocksPerEpoch.Int)   // Q.0
	lam = lam.Lsh(lam, precision)                        // Q.256
	lam = lam.Div(lam /* Q.256 */, totalPower /* Q.0 */) // Q.256
	return lam
}

列成代数表达式可以是这样的:

$\lambda = \frac{blocks\_per\_epoch\ *\ power}{total\_power} * 2^{256}, \{block\_per\_epoch=5\}$

根据前面的内容, 可以知道二项式分布中概率$p$,当重复试验次数n趋于正无穷的时候, 等式成立:$p = \begin{cases}\lim\limits_{n \to \infty}\frac{\lambda}{n}\end{cases}$

所以, 这个$\lambda$的值现在可以认为是在重复$2^{256}$个高度以后, 矿工理论上应该获得的wincount数量(数学期望)

关于$1-CDF[Poisson[\lambda], k]$的意义

对于Filcoin计算Wincount部分的泊松分布, 根据前面的了解,可以知道,

累积分布$CDF[Poisson[\lambda], k]$的意义表示:

当$n \to \infty$时, 矿工出块数为$0 \to k$之间的概率.

故而$1-CDF[Poisson[\lambda], k]$的意义表示:

当$n \to \infty$时, 矿工出块数为$k \to n (n \to \infty)$的概率.

所以在Filcoin计算wincount的下面这一部分代码中:

p, rhs := newPoiss(lam)
var j int64
for lhs.Cmp(rhs) < 0 && j < MaxWinCount {
	rhs = p.next()
	j++
}

newPoisson 返回值rhs, 是计算$1-CDF[Poisson[\lambda], k], \{k=0\}$的值
p.next 返回的rhs, 是计算$1-CDF[Poisson[\lambda], k], \{k=k+1\}$值

再返回来看这段$for(...)$循环, 其功能为:

newPoissn(lam), k=0, 返回出块数$>=1$的概率
p.next(), k=1, 返回出块数$>=2$的概率
p.next(), k=2, 返回出块数$>=3$的概率
....

关于lhs(hash256[VRFProof])的理解

VRFProof是Filcoin的分布式随机数生成服务生成的256bit的随机变量,

由于Filcoin已经把poisson分布中的概率, 映射到了$[0, 2^{256})$之间,概率上可以视为$[0,1)$之间的一个值.

h := blake2b.Sum256(ep.VRFProof)
lhs := BigFromBytes(h[:]).Int // 256bits, assume Q.256 so [0, 1)
...
for lhs.Cmp(rhs) < 0 && j < MaxWinCount {
		rhs = p.next()
		j++
}

这一部分代码可以看成, 分布式随机数生成的服务器在每一轮出块计算时, 给出一个随机概率阈值记为$\phi$,

这个值对于所有的矿工来说都一样, 计算矿工本轮的wincount就是计算:$\max(0, k), k \in (1-CDF[Poisson[\lambda],k] > \phi)$ ,

所以这个wincount在满足条件的情况下, 是符合其出块的数学期望的.

验证Wincount是否符合其算力对等的数学期望

下面的代模拟了证了10万, 100万轮出块, 矿工算力为全网30%情况下, 矿工赢得的wincount:

func TestWinCounts(t *testing.T) {
	totalPower := NewInt(100)
	power := NewInt(30)

	ep := &ElectionProof{VRFProof: nil}

	round := 100000.0
	networkWincount := round * float64(blocksPerEpoch.Int64())
	expectedWincount := networkWincount * 30 / 100
	realWincount := int64(0)
	for i := uint64(0); i < uint64(round); i++ {
		i := i + 1
		ep.VRFProof = []byte{byte(i), byte(i >> 8), byte(i >> 16), byte(i >> 24), byte(i >> 32)}
		j := ep.ComputeWinCount(power, totalPower)
		realWincount += j
	}
	fmt.Printf("round=%d, expected wincount = %d, actually wincount=%d\n",
		int64(round), int64(expectedWincount), realWincount)
}

10万轮的情况, 预期赢票数为150000, 实际赢票为:150031

=== RUN   TestWinCounts
round=100000, expected wincount = 150000, actually wincount=150031
--- PASS: TestWinCounts (0.36s)
PASS

100万轮的情况, 预期赢票为1500000, 实际赢票为:1498847

=== RUN   TestWinCounts
round=1000000, expected wincount = 1500000, actually wincount=1498847
--- PASS: TestWinCounts (3.26s)
PASS

posted on 2021-06-11 09:39 88911562 阅读(242) 评论(0) 编辑收藏举报

刷新页面返回顶部

导航

Filcoin出块权算法原理

排列

组合