题解 CF1909H
题意
给定一个长度为 \(n\) 的排列 \(p\)。你可以进行不超过 \(10^6\) 次操作，每次操作是选择一个长度为偶数的区间 \([l,r]\)，然后交换 \((p_l,p_{l+1}),(p_{l+2},p_{l+3}),...,(p_{r-1},p_r)\)。
你需要将排列排序。
数据范围：\(n \le 3\times 10^5\)。
题解
刚才有个群友问我 Z 菜鸡发生肾摸事了，我说怎么回事？给我发了几张 CF 分数对比图，我一看！嗷！原来是昨天，我打了一场 CF，爆零了，掉分到 newbie，又被嘲讽了。
提供另一种 \(2n\) 次操作的做法。
首先假设 \(n\) 是奇数。
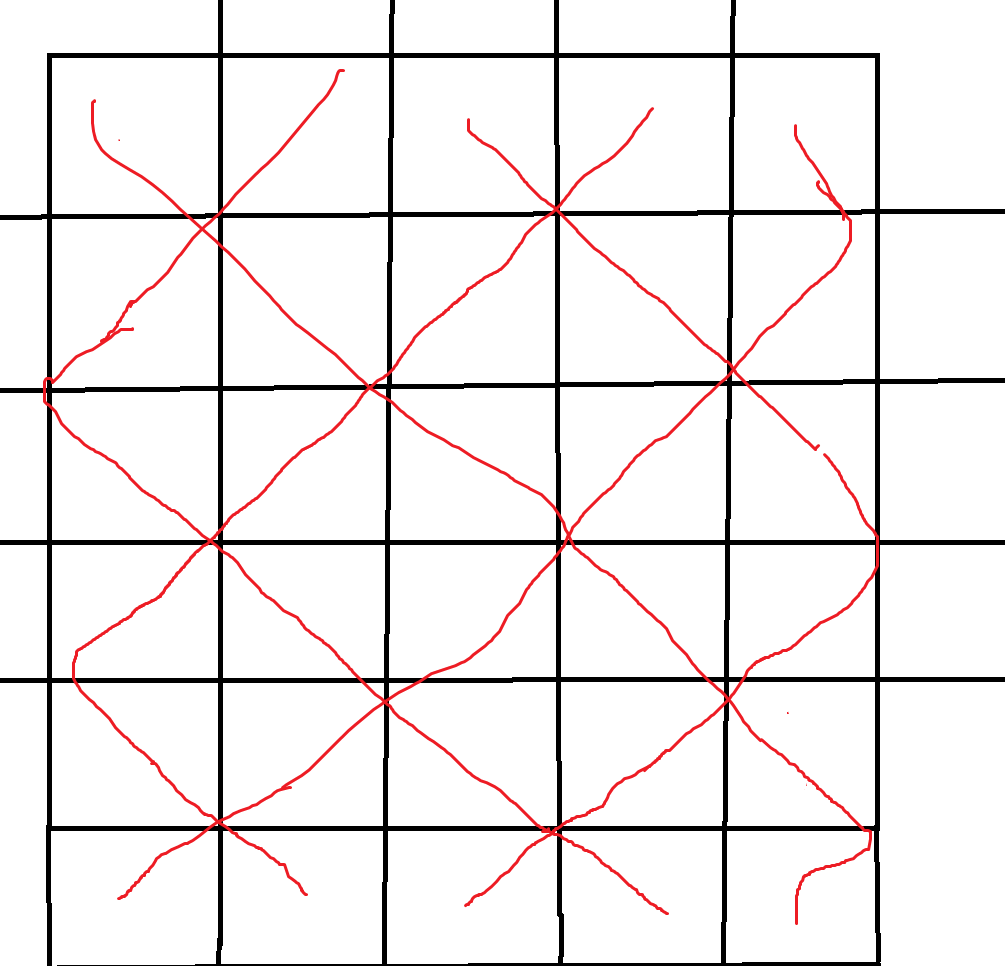
我们考虑交替执行 \((1,n-1)\) 和 \((2,n)\)，执行 \(n\) 次，观察执行后的结果。下面是一张做工粗糙的图：
可以发现第 \(i\) 号位置被交换到了第 \(n-i+1\) 上，而且每两条线路都相交了恰好一次。
不妨称终点在 \(i\) 号点的线路为第 \(i\) 条线路。
在两条线路相交的时，我们可以选择交换这两条线路的起点。考虑在这些操作中加入这些交换来把排列变成 \(p\)。
设 \(to_i = p_{n-i+1}\)，并给 \(i \to to_i\) 连边，连的边形成一些置换环。一条边 \(x\to y\) 表示我们要把第 \(x\) 条线路的起点换到第 \(y\) 条线路上。这时，前文的交换线路可以看成是 每个时刻我们都有机会交换一些 \(to_x\) 和 \(to_y\)，且每对 \((x,y)\) 都出现了恰好一次。
我们遇到一对 \((x,y)\) 的时候，如果 \(x\) 和 \(y\) 在一个置换环上，那么就交换，此时置换环会分裂，\(x\) 和 \(y\) 就不在一个置换环上了。执行完所有交换后，每两个点都不在一个置换环上，因此一定有 \(to_i=i\)。
由于置换环最多分裂 \(n-1\) 次，所以这样做最多操作 \(2n-1\) 次。
然而这还没完：这题 \(n\) 是 \(3\times 10^5\)，所以我们不能暴力做！注意到对于一个置换环，最早的能交换的数对 \((x,y)\) 一定满足 \(x\) 和 \(y\) 在对置换环的节点排序后相邻，所以只要对于每个环维护一个从小指向大的链表，环分裂的时候把小的那边拿出来删掉并重构即可。
\(n\) 是偶数的做法是差不多的，无非是把 \((1,n-1)\) 和 \((2,n)\) 换成 \((1,n)\) 和 \((2,n-1)\)。
时间复杂度 \(\mathcal O(n\log^2 n)\) 或 \(\mathcal O(n \log n)\)，操作次数不超过 \(2n-1\)。
代码。
