联合省选 Day2
T1 卡牌 (easy+)
题意
有 \(n\) 张可以两两区分的卡,第 \(i\) 张卡上写着正整数 \(s_i\)。
有 \(m\) 次查询,每次查询给出 \(c_i\) 个质数,\(p_{i,1},p_{i,2},...,p_{i,c_i}\),询问有多少种选择卡片子集的方法,使得卡片上的数的乘积能被所有给出的质数整除。
数据范围:\(1 \le n \le 10^6\),\(1 \le s_i \le 2000\),\(1 \le m \le 1500\),\(1 \le c_i, \sum_{i} c_i \le 18000\),\(2 \le p_{i,j} \le 2000\)。
题解
考虑把 \(\le 43\) 的质数称为小质数,\(> 43\) 的质数称为大质数。这样一个数不可能被两个大质数整除,并且只有 \(14\) 个小质数。
我们对每个 \(c_i\) 中出现的小质数容斥,钦定一些 \(c_i\) 没有被整除。这样我们就可以去掉对于小质数的限制了,变为只有对大质数的限制。
设对于一个大质数数 \(p\),\(p\) 的倍数的卡牌集是 \(S_p\)。对于每个大质数 \(p\) 都有 \(S_p\) 中的元素只要有一个牌的限制。注意到任意两个 \(S_p\) 都是互不相交的,所以可以对于每个大质数直接把答案乘以 \(\frac{2^{S_p} - 1}{2^{S_p}}\)。
因此我们对于每个钦定不选的小质数集合把 \(|S_p|\) 都预处理出来即可。
所以我们现在的时间复杂度就是 \(\Theta((\max(s_i) + \sum c_i) 2^{14})\)
T2 序列变换 (medium+)
题意
给定一个长度为 \(2n\) 的合法括号序列 \(s\),对于每个 \(s\) 的左括号都有一个权值。你可以进行一下两种操作:
-
选择形如 \(\texttt{(A)(B)}\) 的括号串,然后把他变成 \(\texttt{(A()B)}\),代价为 \(x\) 乘 \(\texttt{(A)}\) 中第一个左括号的权值加上 \(y\) 乘 \(\texttt{(B)}\) 中第一个左括号的权值,其中 \(x, y \in \{0, 1\}\)。
-
交换形如 \(\texttt{pABq}\) 的串中的 \(\texttt{A}\) 和 \(\texttt{B}\),变换为 \(\texttt{pBAq}\),这个操作不需要代价。
这两种操作中的 \(\texttt{A}\) 和 \(\texttt{B}\) 都必须是合法括号串。
求使得序列中没有作形如 \(\texttt{(A)(B)}\) 的括号串的最小代价。
数据范围:\(2 \le n \le 4 \times 10^5\),\(0 \le x,y \le 1\),所有权值在 \([1,10^7]\) 内。
题解
考虑对于括号序列建树。
第一种操作等价于用一个兄弟 \(a\) 把另一个兄弟 \(b\) 换下去,具体来说是这样子的:
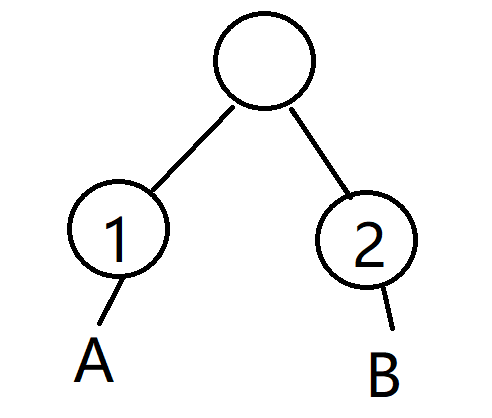
变成
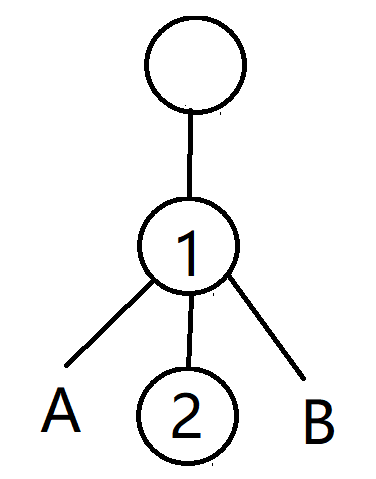
花费的代价是 \(w_a \times x + w_b \times y\)。
第二种操作就是交换两颗子树。因此子树间的顺序是无序的。
这样,恰好有一个点的深度增加了 \(1\)。
考虑一个贪心,按从浅到深的顺序,每次把当前层的节点放到下一层,最后只留下一个节点。这样一定是更优的,因为这样每次可以选择任意两个当前层的节点进行操作,有着最大的操作空间。
现在我们分类讨论。
\(x = 0, y = 0\)
答案显然为 \(0\)。
\(x = 0, y = 1\)
那么这个时候和 \(x\) 没有关系,所以只要每次只把当前权值最大的元素留在这一层就是最优的,用堆维护一下即可。时间复杂度 \(\Theta(n \log n)\)。
\(x = 1, y = 1\)
容易发现,我们的 \(x\) 在还剩 \(> 2\) 个元素的时候一定选择当前最小的元素。而在还剩 \(2\) 个元素的时候把最小的元素换下去一定更优。最后把最大的元素留下来就是最优的了。
这样操作的代价是 \(\sum_{i \in S} w_i + (|S| - 2) \min_{i \in S} w_i\)。
时间复杂度 \(\Theta(n \log n)\)。
\(x = 1, y = 0\)
首先我们找到第一个元素个数不是 \(1\) 的那一层,前面的那些层都是不需要操作的,可以直接丢掉,所以我们不妨第一层的元素个数就 \(> 1\)。
这样除去最后一层,在之后每层操作的过程中,元素个数都 \(> 1\)。
我们考虑每层留下来的是什么元素。如果这一层留下来的元素是 \(w\),那么操作的代价就是 \(w + (|S| - 2) \times \min_{i \in S} w_i\)。
由于最后一层留下来的元素并不需要操作。设最后一层留下来的元素是 \(p\),那么所有 \(w\) 的贡献和就是 \((\sum_{i} w_i) - w_p\)。
因此我们选定了 \(p\) 之后,就先把 \(p\) 从序列中取出,然后再在每层贪心的把最大值留下来即可。
注意到除去 \(p\) 后,如果当前层的元素个数 \(>1\),那么一定可以把最小值留下来。
所以我们找到一个最长的 \(2,1,1,1...\) 的前缀,设长度为 \(l\)。只有 \(l\) 后面的元素才和 \(\min_{i \in S} w_i\) 有关。
如果选择的 \(p\) 在 \(l\) 后面,那么对于每个集合的 \(\min_{i \in S} w_i\) 都能取到最小值。这个时候只要选择最大的 \(p\) 即可。
否则选择了一个这个长为 \(l\) 的前缀中的一个元素 \(p\)。这样,这个前缀中的元素只有 \(p\) 能被推到更深的地方。注意到如果我们选了 \(p\),那么 \(p\) 一定比 \(l\) 后面元素的最大值还要大,否则选 \(p\) 会更劣。所以 \(p\) 一定更新不了 \(l\) 后面元素的最小值。因此我们在这个长度为 \(l\) 的前缀中也只用选择最大的 \(p\)。
这部分的时间复杂度是 \(\Theta(n)\)。
T3 最大权独立集问题 (medium+)
题意
给定一颗二叉树,点 \(i\) 有点权 \(d_i\)。你每次可以删去一条边 \((u,v)\),删去的代价是 \(d_u + d_v\),并交换 \(d_u\) 和 \(d_v\)。求把所有边删掉的最小代价。
数据范围:\(1 \le n \le 5000\),\(1 \le d_i \le 10^9\)。
题解
我们考虑第 \(i\) 个点的子树和父亲交换的是什么。
比如说是子树内第 \(j\) 个点和子树外的第 \(k\) 个点交换,我们可以设计一个 \(\rm DP\) 把 \(j\) 和 \(k\) 都记录下来。这样可以 \(\Theta(n^3)\),能拿 \(44\) 分。
但是我们注意到这个 \(k\) 在子树内被用的次数可能不是很多,所以我们可以记录 \(k\) 在子树内被交换了几次(包括 \(j\) 和 \(k\) 交换)。
设 \(\textrm{DP}_{i,j,k}\) 表示第 \(i\) 个与父亲交换时,将第 \(j\) 个点交换到了子树外,子树外交换到子树内的点在子树内被使用了 \(k\) 次,这个时候在子树内的代价最小是多少(不包含子树外那个点的代价)。
最终要求的答案就是 \(\max(\textrm{DP}_{1,i,1} - d_i)\)。
case1 : \(x\) 没有儿子
显然 \(DP_{x,x,1} = d_i\) 即可。
case2 : \(x\) 只有一个儿子
分两类讨论,\(x\) 和 \(fa_x\) 与 \(x\) 和 \(son\) 之间交换的顺序。
- \(x\) 和 \(fa_x\) 先交换:\(DP_{u,x,i+1} \leftarrow DP_{son,v,i} + d_x\)。
- \(x\) 和 \(son\) 先交换:\(DP_{u,v,1} \leftarrow DP_{son,v,i} + d_{x} \times i + d_v\)。
case3 : \(x\) 有两个儿子
我们分类讨论这个 \(\rm DP\) 怎么转移。我们要考虑的是 \(x\) 和 \(fa_x\) 之间的转移,\(x\) 和 \(ls\) 之间的转移,\(x\) 和 \(rs\) 之间的转移。
不妨先和左儿子交换,\(x\) 先和 \(ls\) 交换的时间比 \(x\) 和 \(rs\) 交换的时间早。
- \(x\) 与 \(fa_x\) 交换,再与 \(ls\) 先交换,再和 \(rs\) 交换:\(DP_{x,x,j + 1} \leftarrow d_x + DP_{ls,i,j} + DP_{rs,k,l} + d_i \times l\)。
- \(x\) 与 \(ls\) 先交换,再与 \(fa_x\) 交换,再和 \(rs\) 交换:\(DP_{x,i,l + 1} \leftarrow DP_{ls,i,j} + d_i + d_x \times j + DP_{rs, k, l}\)。
- \(x\) 与 \(ls\) 先交换,再与 \(rs\) 交换,再和 \(fa_x\) 交换:\(DP_{x,k,1} \leftarrow DP_{ls,i,j} + d_x \times j + d_i \times l + DP_{rs, k, l} + d_k\)
容易发现 \(DP_{x,i,j}\) 中的 \(i\) 如果在左子树中,\(j\) 不会超过 \(dep_{rs}\),如果 \(i\) 在右子树中,\(j\) 不会超过 \(dep_{ls}\)。因此状态数不会超过 \(\Theta(siz_{ls} \times siz_{rs})\) 级别,也就是 \(\Theta(n^2)\)。
由于上述操作我们都可以优化至 \(\Theta(1)\) 转移,因此时间复杂度与空间复杂度均为 \(\Theta(n^2)\)。

