题解-CF1483F Exam[*medium]
题面
给定 \(n\) 个不同的字符串 \(S_1, S_2, ... S_n\),求数对 \((i, j)\) 的个数,满足 \(S_i\) 是 \(S_j\) 的子串,且不存在一个不等于 \(i\) 和 \(j\) 的 \(k\) ,满足 \(S_i\) 是 \(S_k\) 的子串且 \(S_k\) 是 \(S_j\) 的子串。
数据范围:\(n, \sum |S| \le 10^6\)。
题解
我还是学傻了啊,经过神 sjy 的提醒才发现在这儿 \(\rm ACAM\) 和 \(\rm SAM\) 是等价的。
考虑枚举长的字符串,短的字符串必然在长的字符串中出现。
枚举短串的右端点,对答案有贡献的字符串一定是左端点最靠左边的。
然后还要求没有其他的字符串包含这个字符串,可以简单地判掉。
可以结合这张图理解
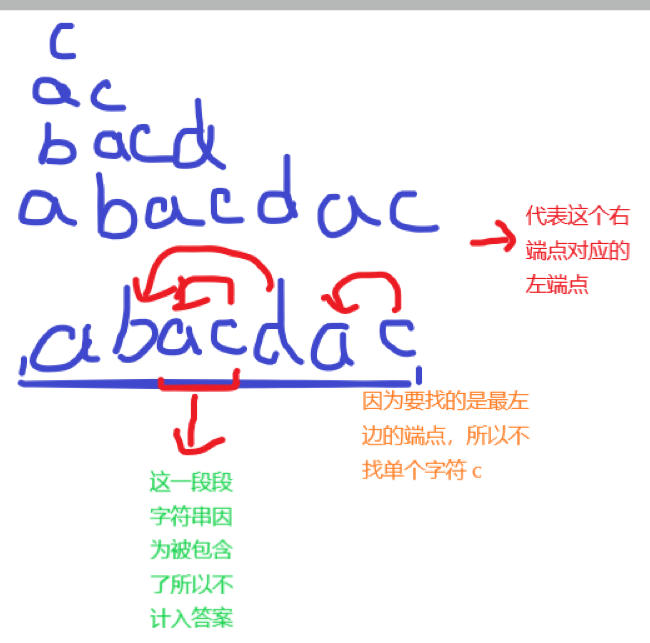
但是这样会算重,如何解决?
发现只有 算到的次数 = 在长串中出现的次数 的情况对答案有 \(1\) 的贡献。
算到的次数可以轻松维护,在长串中出现的次数可以用 树状数组 + ACAM 来维护。时间复杂度和空间复杂度都是 \(\Theta((\sum|S|) \log (\sum|S|))\)。
代码
具体细节见代码
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j, i##E = k; i <= i##E; i++)
#define R(i, j, k) for(int i = j, i##E = k; i >= i##E; i--)
#define ll long long
#define pii pair<int, int>
#define x first
#define y second
#define sz(a) ((int) (a).size())
using namespace std;
const int N = 1e6 + 7;
template<typename T> inline void cmax(T &x, T y) { if(x < y) x = y; }
template<typename T> inline void cmin(T &x, T y) { if(y < x) x = y; }
using namespace std;
int ns, cnt[N], tot, fa[N];
vector< int > change[N], e[N], qet[N];
int ch[N][26], sz[N];
void ad(int x, int y) {
for(; x <= tot + 1; x += (x & -x)) sz[x] += y;
}
int query(int x) {
int res = 0;
for(; x; x -= (x & -x)) res += sz[x];
return res;
}
int qry(int l, int r) {
return query(r) - query(l - 1);
}
int n, m, siz[N], hv[N], St[N], En[N], idtot, mx[N], sx[N], lef[N], sG[N];
void dfs(int x) {
St[x] = ++idtot;
for(int v : e[x]) {
if(!sx[v]) sx[v] = sx[x];
mx[v] = max(mx[v], mx[x]), dfs(v);
}
En[x] = idtot;
}
void ins(string s) {
int now = 0;
L(i, 0, sz(s) - 1) {
if(!ch[now][s[i] - 'a']) ch[now][s[i] - 'a'] = ++tot;
now = ch[now][s[i] - 'a'];
}
}
void build() {
queue<int> q;
L(i, 0, 25) if(ch[0][i]) q.push(ch[0][i]);
while(!q.empty()) {
int u = q.front();
q.pop();
L(i, 0, 25)
if(ch[u][i]) fa[ch[u][i]] = ch[fa[u]][i], q.push(ch[u][i]);
else ch[u][i] = ch[fa[u]][i];
}
}
string s[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
L(i, 1, n) cin >> s[i], ins(s[i]);
L(i, 1, n) {
int now = 0;
L(j, 0, sz(s[i]) - 1) now = ch[now][s[i][j] - 'a'], change[now].push_back(i);
cmax(mx[now], sz(s[i])), sx[now] = now;
}
build();
L(i, 1, tot) e[fa[i]].push_back(i);
dfs(0);
L(i, 1, n) {
L(j, 1, sz(s[i])) qet[j].clear();
int now = 0;
L(j, 0, sz(s[i]) - 1) {
now = ch[now][s[i][j] - 'a'], ad(St[now], 1);
if(j == sz(s[i]) - 1) now = fa[now];
lef[j] = j - mx[now] + 1, sG[j] = sx[now];
}
lef[sz(s[i])] = 1e9;
R(j, sz(s[i]) - 1, 0) {
if(lef[j] <= j && lef[j] < lef[j + 1]) qet[j - lef[j] + 1].push_back(sG[j]);
lef[j] = min(lef[j], lef[j + 1]);
}
L(j, 1, sz(s[i])) {
for(int x : qet[j]) cnt[x] ++;
for(int x : qet[j]) if(cnt[x]) ns += (qry(St[x], En[x]) == cnt[x]),
cnt[x] = 0;
}
now = 0;
L(j, 0, sz(s[i]) - 1) now = ch[now][s[i][j] - 'a'], ad(St[now], -1);
}
cout << ns << "\n";
return 0;
}
祝大家学习愉快!

