CF1266F [*medium]
看到其他题解里面全是什么 bfs 序上线段树啊,什么根号的奇怪东西啊,蒟蒻用了一个非常好写的 \(O(n)\) 做法(这里实现的时候用了 vector,所以比较慢),写篇题解来造福社会
目前在 cf 上是最短解
如果 \(k = 1\),答案是 \(\max(deg_i + 1)\)
考虑有 \(3\) 个点的情况:
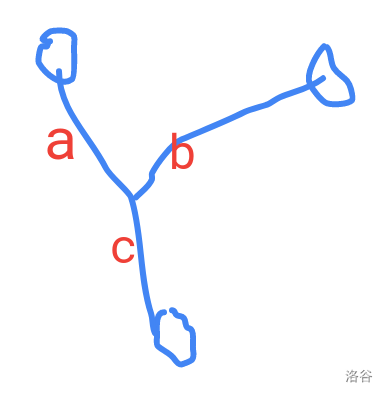
通过放缩法可以证明(证明比较简单而繁琐略去)。考虑在这种情况下的链长(图中的 \(a, b, c\)):
- \(k\) 为奇数:有一个中心结点,旁边的链最多只有一个长为 \(\frac{k-1}{2}\) 的,其他都是 \(\frac{k + 1}{2}\)。
- \(k\) 为偶数:有一个中心结点,旁边的都是长为 \(\frac{k}{2}\) 的链。
但是这样会发现在样例 \(2\) 挂掉了。漏掉了下面的情况:
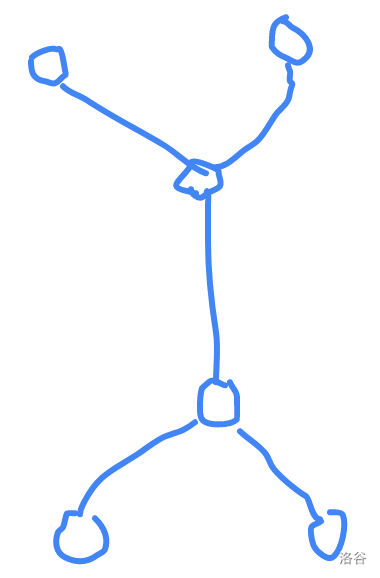
因此有了第 \(3\) 种情况 :在 \(k\) 为偶数的时候,有两个中心结点,旁边链长要求为 \(\frac{k}{2}\)。
在这 \(3\) 种情况下,我们发现一定满足 \(ans_x \ge ans_{x + 2}\)。
对于前两个情况,每一个结点我们记录以他为根时的子树深度,然后把这个深度进行排序。\(k\) 为偶数时第 \(i\) 大数 \(t\) 的则表示 \(ans_{2t} \ge i\) 。奇数稍微麻烦点,第 \(i\) 大数 \(t\) 的则表示 \(ans_{2t-1} \ge i\),如果不和排在前面的数相同,那么我们发现长度为 \(ans_{2t+1} \ge i\)(用这条链和之前面的几条链放在一起,就是长度为 \(t\) 和一堆 \(t + 1\))。这里都很显然。
第 \(3\) 种情况,显然可以把所有相邻的两个位置 \(A\), \(B\) 的子树深度数组给合并在一起,然后再按照第一种情况做就行了,可惜是 \(n^2\) 的。
考虑从后到前,对于这个子树深度数组扫描线,扫到 \(k\) 时更改每一个数的时候判一下和相邻结点的点的和 \(sum - 2\) (\(sum\) 会算到 \(B\) 做 \(A\) 子树和 \(A\) 做 \(B\) 子树的贡献,因此 \(sum\) 要减 \(2\))是否可以更新 \(ans_{k}\)。
这个可以套路地看作是计算父亲结点和子树结点的最大值,额外记录一下子树 \(sum\) 的最大值 \(mxs\),在修改一个结点的时候更新父亲结点的 \(mxs\),同时用 \(max(sum_{fa}, mxs)\) 来更新答案。
具体实现时,第 \(1\) 和第 \(2\) 种情况也可以把排序换成扫描线做到 \(O(n)\)
其余细节见代码。
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j, i##E = k; i <= i##E; i++)
#define R(i, j, k) for(int i = j, i##E = k; i >= i##E; i--)
using namespace std;
const int N = 5e5 + 7;
void Max(int &x, int y) { if(x < y) x = y; }
int n, deg[N], Fa[N], f1[N], f2[N], sum[N], mx1[N], mx2[N], up[N], mxs[N], las, u, v;
vector<int> G[N], e[N];
void dfs1(int x) {
Max(f1[0], deg[x] + 1), mxs[x] = -1e9;
for(int v : e[x]) if(v ^ Fa[x]) {
Fa[v] = x, dfs1(v);
if(mx1[v] + 1 > mx1[x]) mx2[x] = mx1[x], mx1[x] = mx1[v] + 1; else Max(mx2[x], mx1[v] + 1);
}
}
void dfs2(int x) {
if(x ^ 1) G[up[x]].push_back(x);
for(int v : e[x]) if(v ^ Fa[x]) G[mx1[v] + 1].push_back(x);
for(int v : e[x]) if(v ^ Fa[x]) up[v] = max(up[x], mx1[v] + 1 == mx1[x] ? mx2[x] : mx1[x]) + 1, dfs2(v);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n, f1[n] = f2[n] = 1;
L(i, 1, n - 1) cin >> u >> v, deg[u] ++, deg[v] ++, e[u].push_back(v), e[v].push_back(u);
dfs1(1), dfs2(1);
R(i, n, 1) {
las = 0;
for(int t : G[i]) {
sum[t] ++, Max(mxs[Fa[t]], sum[t]);
Max(f2[i], sum[t] + mxs[t] - 2), Max(f2[i], sum[t] + sum[Fa[t]] - 2); // case 3
Max(f2[i], sum[t]); // case 1
Max(f1[i - 1], sum[t]); // case 2
if(las != t) Max(f1[i], sum[t]); las = t; // case 2
}
}
R(i, n, 1) Max(f1[i - 1], f1[i]), Max(f2[i - 1], f2[i]);
L(i, 1, n) cout << (i % 2 ? f1[i / 2] : f2[i / 2]) << " ";
cout << endl;
return 0;
}
祝大家学习愉快!

