题解 CF1428F Fruit Sequences

\(\texttt{Bullshit}\)

蒟蒻 \(\texttt{7 min}\) 切 \(\texttt{F}\), 挽回了本一定掉分的局面/cy

分竟然还没有别人 5 题高

(本题解为目前 cf 上的最短代码解！)

\(\texttt{Solution}\)

考虑计算对于每一个左端点的贡献。

所以可以考虑算这个左端点比后面的那个左端点多了多少贡献。

对于一个位置 \(l\) :

1. 这个位置是 0 : 没有多余贡献。
2. 这个位置是 1 : 如果这个位置到这个联通块底部的长度为 \(k\), 那么找到后面第一个出现连通块长度为 \(k\) 的位置 \(d\)，那么右端点在 \([l, d - 1]\) 的答案都会加一，比左端点为 \(l+1\) 的贡献多了 \(d - l\); 如果找不到，右端点在 \([d, n]\) 的答案都会加一，那么比左端点为 \(l+1\) 的贡献多了 \(n + 1 - l\)。

给一张图以便理解：

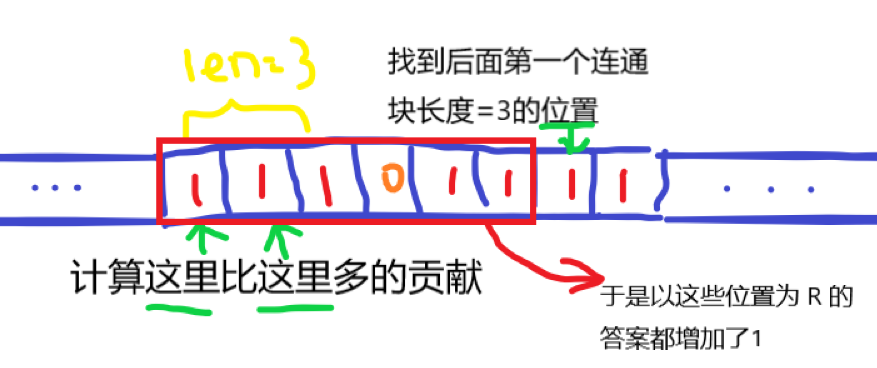
然后考虑怎么维护这东西。

由于我们要找的是第一个出现某联通块长的位置, 那么我们可以在计算完长度为 \(k\), 初始位置为 \(t\) 的连通块的贡献后，从左到右更新联通块长度为 \(1\) 到 \(k\) 的第一次出现的位置。长度为 \(p\) 第一次出现的位置更新为 \(t + p - 1\)。

因此直接用数组维护就好啦！

\(\texttt{Code}\)

不是给人看的代码:

#include<cstdio>
int n,f[555555],now;long long ans,sum;char s[555555];int main(){scanf("%d%s",&n,s+1);for(int i=n;i>=1;i--){if(s[i]-'0')now++,sum+=(!f[now]?n+1:f[now])-i;else while(now)f[now]=i+now,now--; ans+=sum;}printf("%lld\n", ans);}

给人看的代码:

#include<bits/stdc++.h>
const int N = 1e6 + 7;
int n, f[N], now; 
// f[i] : 记录联通块大小为 i 的第一次出现的位置 
// now : 记录现在的连通块大小 
long long  ans, sum;
// ans : 记录答案
// sum : 目前这个左端点的答案 
char s[N];
int main() {
	scanf("%d%s", &n, s + 1);
	for(int i = 1; i <= n; i++) f[i] = n + 1;
	for(int i = n; i >= 1; i--) {
		if(s[i] - '0') now++, sum += f[now] - i; // 联通块大小++, 计算比左端点为 i + 1 的贡献多了多少 
		else while(now) f[now] = i + now, now--; // 一个连通块的结束，更新 f 的值 
		ans += sum; 
	}
	printf("%lld\n", ans);
	return 0;
}