后缀自动机学习笔记
后缀自动机学习笔记
推荐大佬的 \(blog\)
什么是后缀自动机
后缀自动机是在一个 \(DAG\) 图中, 表示出了后缀自动机的所有后缀
显然字典树可以解决,但是字典数的节点数是 \(n^2\) 的。
而后缀自动机可以让节点数量达到线性。
后缀自动机的一个节点代表一个集合,而这个会在后面的集合中提到。
后缀自动机的前置知识
对于一个字串,他在原串中出现了若干次。出现的右端点编号的集合称为 \(endpos\) 集合。\(e.g.\) 原串为 \(abcab\) 时, \(endpos(ab) = {2,5}\)
现在给出几个结论 (不难证明)
1. 如果两个不同子串的 \(endpos\) 集合中有任意一个元素相同,则其中子串一个必然为另一个的后缀
2. 对于任意两个子串 \(a\) 和 \(b\), \(len_a \le len_b\) 要么 \(endpos(a) \in endpos(b)\) ,要么 \(endpos(a) \cap endpos(b) = \emptyset\)
3. 对于 \(endpos\) 相同的子串,我们将它们归为一个 \(endpos\) 等价类。对于任意一个 \(endpos\) 等价类,将包含在其中的所有子串依长度从大到小排序,则每一个子串的长度均为上一个子串的长度减 \(1\) ,且为上一个子串的后缀 (简单来说,一个 \(endpos\) 等价类内的串的长度连续)
4. \(endpos\) 等价类个数级别为 \(O(n)\)
这里要提到一个重要的东西叫做 \(parent\) 树
一个 \(endpos\)集合, 如果要把他分割成几个集合, 每一个集合对应一个 \(endpos\) 等价类 (因为 \(endpos\) 等价类如果不是包含关系, 就不能有相同元素。所以只能把一个 \(endpos\) 集合分割成多个 \(endpos\) 集合,然后在其中继续分割。)
于是这就是一个树形结构, 称其为 \(parent\) 树
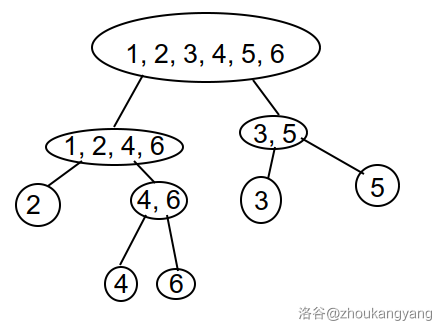
以上图片是一个字符串为 \(aababa\) 的例子
在一个 \(endpos\) 等价类 \(a\) 中, 有最长的串, 同时也有最短的串。设该 \(endpos\) 等价类在\(parent\) 树上的节点的父亲为 \(fa(a)\), 设最长的字串长度是 \(len(a)\), 最短的是 \(minlen(a)\), 那么 \(minlen(fa(a)) + 1= len(a)\)
附上一张在 \(endpos\) 等价类中的最长字串的图片
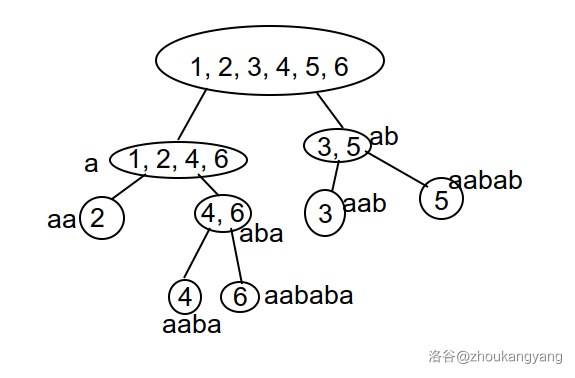
这时, 我们的后缀自动机的节点就是这 \(parent\) 树上的节点!
但是, 后缀自动机的边不同于 \(parent\) 树上的边。
建立一个后缀自动机
先放代码
void ins(int x) {
int p = las, now = las = ++tot;
cnt[now] = 1, f[now].len = f[p].len + 1;
for(; p && !f[p].ch[x]; p = f[p].fa) f[p].ch[x] = now;
if(!p) f[now].fa = 1;
else {
int pto = f[p].ch[x];
if(f[pto].len == f[p].len + 1) f[now].fa = pto;
else {
int sp = ++tot;
f[sp] = f[pto], f[sp].len = f[p].len + 1;
f[now].fa = f[pto].fa = sp;
for(; p && f[p].ch[x] == pto; p = f[p].fa) f[p].ch[x] = sp;
}
}
}
如果在原来的后缀自动机中增加一个字符 \(x\), 那么原串的后缀要增加一个字符 \(x\)
他出现的次数为 \(1\), 而且他的最长字串是原来的后缀长度 \(+1\)
于是有代码
int p = las, now = las = ++tot; // p 是原来的最长后缀,now是现在的最长后缀,las是记录上次最长后缀的
cnt[now] = 1, f[now].len = f[p].len + 1; // len 同上面的描述,是最长字串长度, f是表示parent树的一个endpos等价类的集合, 一个后缀自动机的节点
然后包含之原来的 \(las\) 的节点都被其 \(parent\) 树上的父亲节点所包含, 因此如果在他们的后面再新增一个字符 \(x\), 都会跳到该节点。但是如果他的父亲已经有转移了, 那么就不用再增加这条边了。而且如果遇到一个节点已经有字符 \(x\) 的转移边了, 他的父亲一定也有字符 \(x\) 的转移边, 所以就不用继续往上跳了。
代码:
for(; p && !f[p].ch[x]; p = f[p].fa) f[p].ch[x] = now;
考虑如何在\(parent\) 树上处理 \(now\) 的父亲指针。
如果一直往上跳的过程中, 所有节点都没有向字符 \(x\) 的转移边, 就说明字符 \(x\) 是第一次出现(因为根结点也没有字符 \(x\) 的转移边), 所以除了根结点没有集合能够包含集合编号为 \(now\) 的节点了, 于是其父亲指针指向 \(1\)
if(!p) f[now].fa = 1;
否则 \(p\) 就在有转移边 \(x\) 的祖先节点上停下来了。
这时 \(p\) 是原来 \(las\) 的后缀, 都加上一个字符 \(x\) 之后, \(pto\) (假设点 \(p\) 加上一个 \(c\) 得到了 \(pto\)) 也是 \(now\)的后缀。 都是如果该节点 \(p\) 增加一个 \(x\) 得到的最长后缀恰好是原来后缀的最长后缀的长度\(+1\), 那么就说明了再这个节点代表的所有字串中增加一个 \(x\) 后到达 \(p\) 的 \(endpos\) 一致, 而 \(p\) 又是跳父亲时第一个遇见的节点, 所以 \(pto\) 一定是 \(now\) 的最长后缀, \(now\) 在 \(parent\) 树上的父亲就是 \(pto\)。
int pto = f[p].ch[x];
if(f[pto].len == f[p].len + 1) f[now].fa = pto;
那么 \(len(p) > len(pto) + 1\) 怎么办?
\(len(p) > len(pto) + 1\) 代表了这个串不是 \(now\) 的子串。 因为如果是, 那么最后一个字符就是 \(x\), 然而去掉这个字符就变成了 \(p\) 的字串, 所以 \(len(p) = len(pto) + 1\), 矛盾, 所以这个串必定不是 \(now\) 的子串。所以我们还需要另外一个节点 \(sp\), 从 \(pto\) 复制下他的信息。其 \(len\) 值恰好等于 \(len(pto) + 1\), 代表在原来的 \(p\) 的最大长度代表的串后面增加一个 \(x\)。 这时可以和上面做类似的操作, 让 \(now\) 的父亲变成 \(sp\), 这时可以发现, \(p\) 是 \(pto\) 的后缀, \(p\) 是 \(sp\) 的后缀, 而 \(pto\) 的 \(len > sp\) 的 \(len\) 值, 所以可以让 \(pto\) 的 \(fa\) 值也指向 \(sp\)。由于这时 \(sp\) 的长度更短, 所以需要让原先 \(parent\) 树上儿子节点指向 \(pto\) 的改指向 \(sp\)。
Code:
int sp = ++tot;
f[sp] = f[pto], f[sp].len = f[p].len + 1;
f[now].fa = f[pto].fa = sp;
for(; p && f[p].ch[x] == pto; p = f[p].fa) f[p].ch[x] = sp;
upd
后缀自动机性质:
- \(DAG\) :
ch[x][y]可以表达 \(x\) 这个状态能不能继续往下走 - \(parent\) 树的
fa[x]一定是x的后缀。
常见套路有用 \(SAM\) 建后缀树 (就是 \(parent \ tree\) 啊!),用线段树合并维护 \(endpos\) 等。

