P1939 矩阵加速（数列）

       这个题若不看题目和范围，我首先想到用递推，不过   n≤2×10^9，若用递推，一定会超时。

要用矩阵加速的话首先要找到一个矩阵（不唯一），用来相乘；

〔a1，a2，a3〕是一个1×3的矩阵，我想把它转化为〔a2，a3，a4〕也是一个1×3的矩阵，所以要找的矩阵肯定是3×3的；

可以假设这个3×3的矩阵为 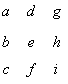      所以 a2=a1×a+a2×b+a3×c 所以a=0；b=1；c=0；同理可得d=0；e=0；f=1；

 

 

a4=a3+a1 所以 g=1；h=0；i=1；所以3×3的矩阵应为     可以看出若想得出an，则需要这个矩阵的（n-3）次方再乘

〔a1，a2，a3〕因为a1，a2，a3都为1，所以可以不用乘，最后得出〔a n-2，a n-1，a n〕；用 r[4][4]来存储乘完后的3×3矩阵，

则an就是 r[1][3]+r[2][3]+r[3][3];通过快速幂就能快速求出答案了。

 

 

其实这个题套用 P 3390 矩阵快速幂的代码就可以，所以我就不再解释了，关于矩阵如何快速幂的问题在上一篇博客(☜点他)已说明。

直接上完整代码：

 

#include<iostream>
using namespace std;
struct hls{
    long long s[4][4];
};
hls t,r;
long long k;
const long long m=1000000007;
hls operator * (const hls &a,const hls &b)
{
    hls w;
    for(int i=1;i<=3;++i)
    {
        for(int j=1;j<=3;++j)
        {
            w.s[i][j]=0;
        }
    }
    for(int x=1;x<=3;++x)
    {
        for(int y=1;y<=3;++y)
        {
            for(int z=1;z<=3;++z)
            {
                w.s[x][y]+=(a.s[x][z]%m)*(b.s[z][y]%m);
                w.s[x][y]%=m;
            }
        }
    }
    return w;
}
int main()
{
    int q;
    cin>>q;
    while(q--)
    {
        cin>>k;
        for(int i=1;i<=3;++i)
        {
            for(int j=1;j<=3;++j)
            {
                t.s[i][j]=0;
                if(i!=j) r.s[i][j]=0;
                else r.s[i][j]=1;
            }
        }
        t.s[1][3]++; 
        t.s[2][1]++; 
        t.s[3][2]++; 
        t.s[3][3]++;
        k=k-3;
        while(k>0) 
        {
            if(k%2==1) r=r*t;
            t=t*t;
            k/=2;
        }
        cout<<(r.s[1][3]+r.s[2][3]+r.s[3][3])%m<<endl;
    }
    return 0;
}