斐波那契数列 --- 四层优化

斐波那契数列

 

起源

兔子问题：“假定一对大兔子每月能生一对小兔子，且每对新生的小兔子经过一个月可以长成一对大兔子,具备繁殖能力，如果不发生死亡，且每次均生下一雌一雄，问一年后共有多少对兔子？”

分析:第一个月兔子没有繁殖能力,所以还是一对;两个月后生下一对兔子,共有两对;三个月后,老兔子生下一对,小兔子还没有繁殖能力,所以一共是三对,以此类推,可以列出下表

表中1,1,2,3,5,8,13.....构成一个序列,这个数列有一个特点就是前两项之和等于后一项

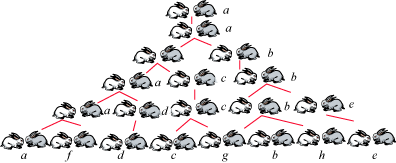
数学函数定义:

---

 

方法1（递归）

时间复杂度：O（N²），空间复杂度：O（N）

long long Fibonacci(unsigned int n)
{
    return n < 2 ? n : Fibonacci(n - 1) + Fibonacci(n - 2);
}

 

方法2（循环）

时间复杂度：O（N），时间复杂度：O（1）

long long Fibonacci(unsigned int n)
{
    int result[2] = { 0, 1 };
    if (n < 2)
        return result[n];

    long long fibNOne = 1, fibNTwo = 0, fibN = 0;
    for (int i = 1; i < n; i++)
    {
        fibN = fibNOne + fibNTwo;
        fibNTwo = fibNOne;
        fibNOne = fibN;
    }
    return fibN;
}

 

方法3（通项公式）

时间复杂度：O（logn），空间复杂度：O（1）

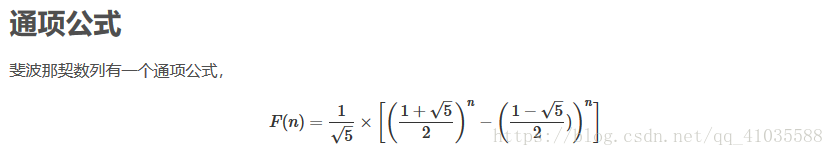
long long Fibonacci(unsigned int n)
{
    return (pow((1 + sqrt(5)) / 2, n) - pow((1 - sqrt(5)) / 2, n)) / sqrt(5);
}

 

方法4（矩阵乘法实现，最优解）

时间复杂度：O（logn），空间复杂度：O（1）

#include<iostream>
#include<string>
using namespace std;

//定义2×2矩阵；
struct Matrix2by2
{
    //构造函数
    Matrix2by2
    (
        long m_00,
        long m_01,
        long m_10,
        long m_11
    )
        :m00(m_00), m01(m_01), m10(m_10), m11(m_11)
    {
    }

    //数据成员
    long m00;
    long m01;
    long m10;
    long m11;
};

//定义2×2矩阵的乘法运算
Matrix2by2 MatrixMultiply(const Matrix2by2& matrix1, const Matrix2by2& matrix2)
{
    Matrix2by2 matrix12(1, 1, 1, 0);
    matrix12.m00 = matrix1.m00 * matrix2.m00 + matrix1.m01 * matrix2.m10;
    matrix12.m01 = matrix1.m00 * matrix2.m01 + matrix1.m01 * matrix2.m11;
    matrix12.m10 = matrix1.m10 * matrix2.m00 + matrix1.m11 * matrix2.m10;
    matrix12.m11 = matrix1.m10 * matrix2.m01 + matrix1.m11 * matrix2.m11;
    return matrix12;

}


//定义2×2矩阵的幂运算
Matrix2by2 MatrixPower(unsigned int n)
{
    Matrix2by2 matrix(1, 1, 1, 0);
    if (n == 1)
    {
        matrix = Matrix2by2(1, 1, 1, 0);
    }
    else if (n % 2 == 0)
    {
        matrix = MatrixPower(n / 2);
        matrix = MatrixMultiply(matrix, matrix);
    }
    else if (n % 2 == 1)
    {
        matrix = MatrixPower((n - 1) / 2);
        matrix = MatrixMultiply(matrix, matrix);
        matrix = MatrixMultiply(matrix, Matrix2by2(1, 1, 1, 0));
    }
    return matrix;
}
//计算Fibnacci的第n项
long Fibonacci(unsigned int n)
{
    if (n == 0)
        return 0;
    if (n == 1)
        return 1;

    Matrix2by2 fibMatrix = MatrixPower(n - 1);
    return fibMatrix.m00;

}

int main()
{
    cout << "Enter A Number:" << endl;
    unsigned int number;
    cin >> number;
    cout << Fibonacci(number) << endl;
    return 0;
}

 

 

斐波那契数列的应用题：

1 青蛙跳台阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法。

提示：f(n) = f(n-1) + f(n-2)

扩展题：

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶......也可以跳上n级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法。

提示：f(n) = 2^n-1

2 如果我们用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问8个2*1的小矩形无重叠地覆盖一个2*8的大矩形，总共有多少种方法？

提示：f(8) = f(7) + f(6)

 

参考：

https://blog.csdn.net/qq_41035588/article/details/81814547