第 118 场双周赛（单调队列 + dp）

 简单模拟即可:

class Solution {
public:
    vector<int> findWordsContaining(vector<string>& words, char x) {
        int n = words.size();
        vector<int> res;
        for(int i = 0; i < n; i ++ ) {
            auto &word = words[i];
            for(auto ch: word) {
                if(ch == x) {
                    res.push_back(i);
                    break;
                }
            }
        }

        return res;
    }
};

 

 

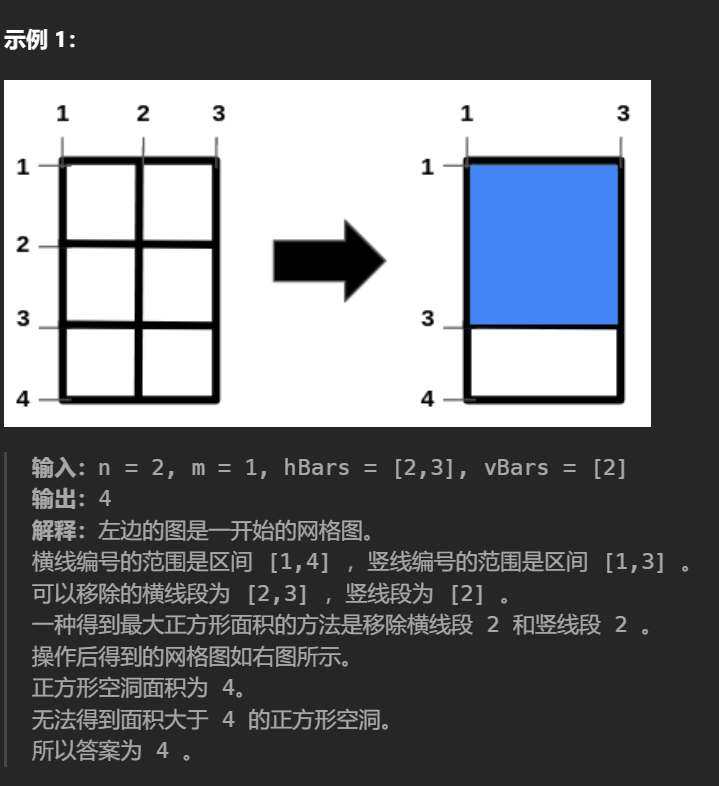
 找规律， 最长连续子序列

class Solution {
public:
    int maximizeSquareHoleArea(int n, int m, vector<int>& hBars, vector<int>& vBars) {
        int res = 0;

        int lh = hBars.size(), lv = vBars.size();
        sort(hBars.begin(), hBars.end());
        sort(vBars.begin(), vBars.end());

        vector<int> f(lh, 1);
        vector<int> g(lv, 1);

        for(int i = 1; i < lh; i ++ ) {
            if(hBars[i] == hBars[i - 1] + 1) {
                f[i] = f[i - 1] + 1;
            }
        }

        for(int i = 1; i <lv; i ++ ) {
            if(vBars[i] == vBars[i - 1] + 1) {
                g[i] = g[i - 1] + 1;
            }
        }

        int vlen = 0, hlen = 0;
        for(int i = 0; i < lh; i ++ ) {
            if(hBars[i] != n + 2) vlen = max(vlen, f[i]);
            else vlen = max(vlen, f[i] - 1);
        }

        for(int i = 0; i < lv; i ++ ) {
            if(vBars[i] != m + 2) hlen = max(hlen, g[i]);
            else hlen = max(hlen, g[i] - 1);
        }

        cout << vlen << ' ' << hlen << endl;
        int lim = min(vlen, hlen);

        return (lim + 1) * (lim + 1);
    }
};

 

 递归搜索 -> 递推 -> 单调队列优化dp

class Solution:
    def minimumCoins(self, prices: List[int]) -> int:
        n = len(prices)

        @cache
        def dfs(i: int) -> int:
            if i > n:
                return 0
            res = inf
            for j in range(i + 1, i * 2 + 2):
                res = min(res, dfs(j))
            
            return res + prices[i - 1]

        return dfs(1)

 

class Solution:
    def minimumCoins(self, prices: List[int]) -> int:
        n = len(prices)
        f = [0] * (n + 1)

        for i in range(n, 0, -1):
            if i * 2 >= n:
                f[i] = prices[i - 1]
            else:
                f[i] = min(f[i + 1: i * 2 + 2]) + prices[i - 1]

        return f[1]
            

 

class Solution:
    def minimumCoins(self, prices: List[int]) -> int:
        n = len(prices)
        q = deque([(n + 1, 0)])

        for i in range(n, 0, -1):
            while q[-1][0] > 2 * i + 1:
                q.pop()
            
            f = q[-1][1] + prices[i - 1]

            while f <= q[0][1]:
                q.popleft()
            q.appendleft((i, f))

        return q[0][1]

 

 

 

单调队列优化dp

f[i] 表示以第i个位置为结尾，操作前i个数字所得到的最大非递减子数组长度

f[i] = f[j] + 1 // f[i] 铁定递增

last[i] 表示这个操作后，最后一个数字最小，有一个小小的贪心，在f[i]尽量大的情况下，last[i]尽量小

s[i] 表示 nums 的前缀和， s[i] - s[j] 表示从j + 1 到 i的元素和

要满足 s[i] - s[j] >= last[j] 才可以转移

 

转移条件

s[i] - s[j] >= last[j] -> s[i] >= s[j] + last[j]

f[i] = f[j] + 1

 

对于两个下标j < k & f[j] < f[k]

s[j] + last[j] < s[k] + last[k] <= s[i]

我们一定是要k这个点对应的数据， 都可以满足条件的情况下，取最大的

 

单调队列优化核心: 剔除无用数据

三部曲:

队首出队条件 （转移之前剔除）

s[j] + last[j] < s[k] + last[k] <= s[i]

队首的第二个下标s[idx] + last[idx] <= s[i] 这时候可以去掉队首

 

转移

f[i] = f[q[0]] + 1

last[i] = s[i] - s[q[0]]

 

队尾入队条件 （转移之后剔除）

s[j] + last[j] < s[k] + last[k] <= s[i]

右边的更大，就可以去掉队尾

 

class Solution:
    def findMaximumLength(self, nums: List[int]) -> int:
        n = len(nums)
        s = list(accumulate(nums, initial=0))
        f = [0] * (n + 1)
        last = [0] * (n + 1)
        q = deque([0])

        for i in range(1, n + 1):
            while len(q) > 1 and s[q[1]] + last[q[1]] <= s[i]:
                q.popleft()
            
            f[i] = f[q[0]] + 1
            last[i] = s[i] - s[q[0]]

            while q and s[q[-1]] + last[q[-1]] >= s[i] + last[i]:
                q.pop()
            q.append(i)

        return f[n]