dfs思想方式

dfs 深度优先搜索：一条路走到黑

基本模型:

Returntype dfs(参数) {
　　判断边界（返回）
　　扩展状态 dfs下一步
　　返回
}

dfs + 记忆返回值 = 记忆化搜索

 

 

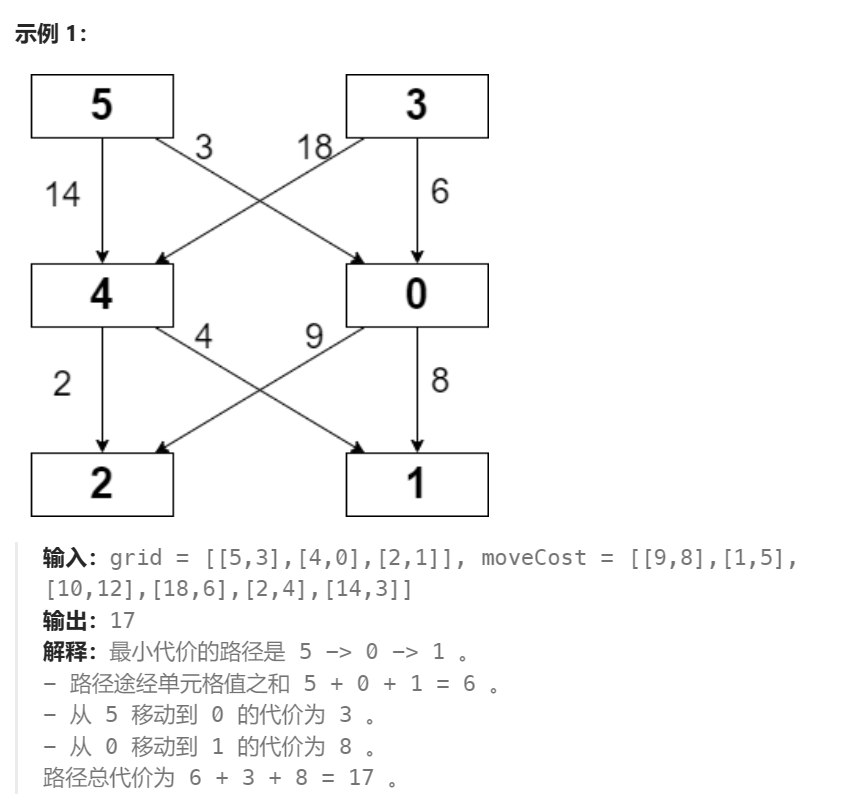
class Solution {
public:
    int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> memo(m, vector<int>(n, -1));

        function<int(int, int)> dfs = [&](int i, int j) ->int {
            if(i == m - 1) return grid[i][j];
            if(memo[i][j] >= 0) return memo[i][j];
            int res = INT_MAX;
            for(int k = 0; k < n; k ++ ) {
                res = min(res, dfs(i + 1, k) + moveCost[grid[i][j]][k] + grid[i][j]);
            }
            memo[i][j] = res;
            return res;
        };

        int res = INT_MAX;
        for(int j = 0; j < n; j ++ ) {
            res = min(res, dfs(0, j));
        }

        return res;
    }
};