java中常见的几种排序算法
---恢复内容开始---
1. 什么是队列、栈、链表?
队列:队列即按照数据到达的顺序进行排队,每次新插入一个节点,将其插到队尾;每次只有对头才能出队列。是一种“先进先出”(FIFO)的数据结构。
栈:栈是一种只能在一端进行插入和删除操作的特殊线性表。它按照先进后出(FILO)的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来),可以理解为一个储物的地方,且只有一个出口,先放进去的东西最后才能拿出来。
链表:链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构,操作复杂。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)
2. 什么是树(平衡树,排序树,B树,B+树,R树,红黑树)、堆(大根堆、小根堆)、图(有向图、无向图、拓扑)
树:平衡二叉搜索树:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
红黑树(Red Black Tree):是一种自平衡二叉查找树 ,红黑树和AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
(1) 每个节点或者是黑色,或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!]
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
B树(多叉排序树):
1、根结点至少有两个子女;
2、每个非根节点所包含的关键字个数 j 满足:m/2 - 1 <= j <= m - 1;
3、除根结点以外的所有结点(不包括叶子结点)的度数正好是关键字总数加1,故内部子树个数 k 满足:m/2<= k <= m ;
4、所有的叶子结点都位于同一层。
R树:
小根堆:最小堆,是一种经过排序的完全二叉树,其中任一非终端节点的数据值均不大于其左子节点和右子节点的值。
图:有向图:一个有向图D是指一个有序三元组(V(D),A(D),ψD),其中ψD)为关联函数,它使A(D)中的每一个元素(称为有向边或弧)对应于V(D)中的一个有序元素(称为顶点或点)对
无向图:边没有方向的图称为无向图。
无向图G=<V,E>,其中:
1.V是非空集合,称为顶点集。
2.E是V中元素构成的无序二元组的集合,称为边集
3. 栈和队列的相同和不同之处 ?
共同点:都是只允许在端点处插入和删除元素的数据结构;
不同点:栈是仅在栈顶进行访问,遵循后进先出的原则(LIFO);队列是在队尾插入数据,在队头删除数据(FIFO)
4. 栈通常采用的两种存储结构 ?
链接存储:链栈 带有头指针或头结点的单循环链表。
顺序存储:数组实现
5. 排序都有哪几种方法?
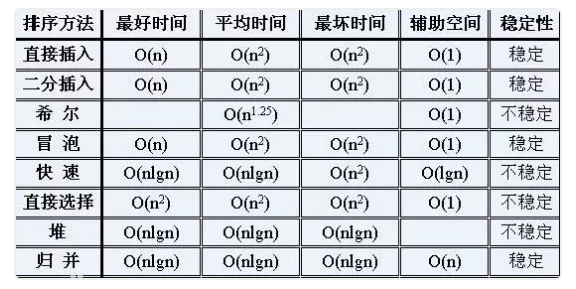
(1) 冒泡排序:
public static void bubbleSort(Comparable[] a) { int j, flag;Comparable temp; for (int i = 0; i < a.length; i++) { flag = 0; for (j = 1; j < a.length - i; j++) { if (a[j].compareTo(a[j - 1]) < 0) { temp = a[j]; a[j] = a[j - 1]; a[j - 1] = temp; flag = 1; } } // 如果没有交换,代表已经排序完毕,直接返回 if (flag == 0) { return; } } }
(2) 插入排序
public static void insertionSort(Comparable[] a) { int length = a.length; Comparable temp; for (int i = 1; i < length; i++) { for (int j = i; j > 0 && a[j].compareTo(a[j - 1]) < 0; j--) { temp = a[j]; a[j] = a[j - 1]; a[j - 1] = temp; } } }// 对实现Comparable的类型进行排序,先将大的元素都向右移动,减少一半交换次数 public static void insertionSort(Comparable[] a) { int length = a.length; Comparable temp; int j; for (int i = 1; i < length; i++) { temp = a[i]; for (j = i; j > 0 && temp.compareTo(a[j - 1]) < 0; j--) { a[j] = a[j - 1]; } a[j] = temp; } }// 二分插入排序,使用二分查找找到插入点,然后进行移位 public static void insertionSort(Comparable[] a) { int length = a.length; Comparable temp; int j; for (int i = 1; i < length; i++) { if (a[i].compareTo(a[i - 1]) < 0) { temp = a[i]; int index = binarySearch(a, a[i], 0, i - 1); for (j = i - 1; j >= index; j--) { a[j + 1] = a[j]; } a[index] = temp; } } } private static int binarySearch(Comparable[] a, Comparable target, int start, int end) { int mid; while (start <= end) { mid = (start + end) >> 1; if (target.compareTo(a[mid]) < 0) { end = mid - 1; } else { start = mid + 1; } } return start; }
(3) 选择排序
public static void selectionSort1(Comparable[] a) { int length = a.length; int min; Comparable temp; for (int i = 0; i < length; i++) { min = i; for (int j = i + 1; j < length; j++) { if (a[j].compareTo(a[min]) < 0) { min = j; } } temp = a[min]; a[min] = a[i]; a[i] = temp; } }
(4) 希尔排序
public static void shellSort(Comparable[] a) { int length = a.length; int h = 1; Comparable temp; while (h < length / 3) { h = 3 * h + 1; } while (h >= 1) { for (int i = h; i < length; i++) { for (int j = i; j >= h && a[j].compareTo(a[j - h]) < 0; j -= h) { temp = a[j]; a[j] = a[j - h]; a[j - h] = temp; } } h /= 3; } }
(5) 堆排序
public static void heapSort(Comparable[] a) { int length = a.length; Comparable temp; for (int k = length / 2; k >= 1; k--) { sink(a, k, length); } while (length > 0) { temp = a[0]; a[0] = a[length - 1]; a[length - 1] = temp; length--; sink(a, 1, length); } } private static void sink(Comparable[] a, int k, int n) { Comparable temp; while (2 * k <= n) { int j = 2 * k; if (j < n && a[j - 1].compareTo(a[j]) < 0) { j++; } if (a[k - 1].compareTo(a[j - 1]) >= 0) { break; } temp = a[k - 1]; a[k - 1] = a[j - 1]; a[j - 1] = temp; k = j; } }
(6) 归并排序
private static Comparable[] aux;// 自顶向下 public static void mergeSort(Comparable[] a) { aux = new Comparable[a.length]; mergeSort(a, 0, a.length - 1); } public static void mergeSort(Comparable[] a, int lo, int hi) { if (hi <= lo) { return; } int mid = (lo + hi) >>> 1; mergeSort(a, lo, mid); mergeSort(a, mid + 1, hi); merge(a, lo, mid, hi); } public static void merge(Comparable[] a, int lo, int mid, int hi) { int i = lo, j = mid + 1; for (int k = lo; k <= hi; k++) { aux[k] = a[k]; } for (int k = lo; k <= hi; k++) { if (i > mid) { a[k] = aux[j++]; } else if (j > hi) { a[k] = aux[i++]; } else if (aux[j].compareTo(aux[i]) < 0) { a[k] = aux[j++]; } else { a[k] = aux[i++]; } } }
自底向上的归并排序
private static Comparable[] aux;// 自底向上 public static void mergeSort(Comparable[] a) { int length = a.length; aux = new Comparable[length]; for (int sz = 1; sz < length; sz = sz + sz) { for (int lo = 0; lo < length - sz; lo += sz + sz) { merge(a, lo, lo + sz - 1, Math.min(lo + sz + sz - 1, length - 1)); } } } public static void merge(Comparable[] a, int lo, int mid, int hi) { int i = lo, j = mid + 1; for (int k = lo; k <= hi; k++) { aux[k] = a[k]; } for (int k = lo; k <= hi; k++) { if (i > mid) { a[k] = aux[j++]; } else if (j > hi) { a[k] = aux[i++]; } else if (aux[j].compareTo(aux[i]) < 0) { a[k] = aux[j++]; } else { a[k] = aux[i++]; } } }
(7) 快速排序
public static void quickSort(Comparable[] a) { quickSort(a, 0, a.length - 1); } public static void quickSort(Comparable[] a, int lo, int hi) { if (hi <= lo) { return; } int j = partition(a, lo, hi); quickSort(a, lo, j - 1); quickSort(a, j + 1, hi); } public static int partition(Comparable[] a, int lo, int hi) { int i = lo, j = hi + 1; Comparable temp; Comparable v = a[lo]; while (true) { while (a[++i].compareTo(v) < 0) { if (i == hi) { break; } } while (v.compareTo(a[--j]) < 0) { if (j == lo) { break; } } if (i >= j) { break; } temp = a[i]; a[i] = a[j]; a[j] = temp; } temp = a[lo]; a[lo] = a[j]; a[j] = temp; return j; }
6. 常见Hash算法,哈希的原理和代价?
散列表,它是基于快速存取的角度设计的,也是一种典型的“空间换时间”的做法。顾名思义,该数据结构可以理解为一个线性表,但是其中的元素不是紧密排列的,而是可能存在空隙。
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
比如我们存储70个元素,但我们可能为这70个元素申请了100个元素的空间。70/100=0.7,这个数字称为负载因子。我们之所以这样做,也是为了“快速存取”的目的。我们基于一种结果尽可能随机平均分布的固定函数H为每个元素安排存储位置,这样就可以避免遍历性质的线性搜索,以达到快速存取。但是由于此随机性,也必然导致一个问题就是冲突。所谓冲突,即两个元素通过散列函数H得到的地址相同,那么这两个元素称为“同义词”。这类似于70个人去一个有100个椅子的饭店吃饭。散列函数的计算结果是一个存储单位地址,每个存储单位称为“桶”。设一个散列表有m个桶,则散列函数的值域应为[0,m-1]。
解决冲突是一个复杂问题。冲突主要取决于:
(1)散列函数,一个好的散列函数的值应尽可能平均分布。
(2)处理冲突方法。
(3)负载因子的大小。太大不一定就好,而且浪费空间严重,负载因子和散列函数是联动的。
解决冲突的办法:
(1)线性探查法:冲突后,线性向前试探,找到最近的一个空位置。缺点是会出现堆积现象。存取时,可能不是同义词的词也位于探查序列,影响效率。
(2)双散列函数法:在位置d冲突后,再次使用另一个散列函数产生一个与散列表桶容量m互质的数c,依次试探(d+n*c)%m,使探查序列跳跃式分布。
常用的构造散列函数的方法:
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快地定位:
1. 直接寻址法:取关键字或关键字的某个线性函数值为散列地址。即H(key)=key或H(key) = a•key + b,其中a和b为常数(这种散列函数叫做自身函数)
2. 数字分析法:分析一组数据,比如一组员工的出生年月日,这时我们发现出生年月日的前几位数字大体相同,这样的话,出现冲突的几率就会很大,但是我们发现年月日的后几位表示月份和具体日期的数字差别很大,如果用后面的数字来构成散列地址,则冲突的几率会明显降低。因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。
3. 平方取中法:取关键字平方后的中间几位作为散列地址。
4. 折叠法:将关键字分割成位数相同的几部分,最后一部分位数可以不同,然后取这几部分的叠加和(去除进位)作为散列地址。
5. 随机数法:选择一随机函数,取关键字的随机值作为散列地址,通常用于关键字长度不同的场合。
6. 除留余数法:取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 H(key) = key MOD p, p<=m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。对p的选择很重要,一般取素数或m,若p选的不好,容易产生同义词。
7. 一致性Hash算法?
一致性哈希算法(Consistent Hashing Algorithm)是一种分布式算法,常用于负载均衡。Memcached client也选择这种算法,解决将key-value均匀分配到众多Memcached server上的问题。它可以取代传统的取模操作,解决了取模操作无法应对增删Memcached Server的问题(增删server会导致同一个key,在get操作时分配不到数据真正存储的server,命中率会急剧下降)。
简单来说,一致性哈希将整个哈希值空间组织成一个虚拟的圆环,如假设某哈希函数H的值空间为0 - (2^32)-1(即哈希值是一个32位无符号整形),整个哈希空间环如下:
(1) 首先求出memcached服务器(节点)的哈希值,并将其配置到0~232的圆(continuum)上。
(2) 然后采用同样的方法求出存储数据的键的哈希值,并映射到相同的圆上。
(3) 然后从数据映射到的位置开始顺时针查找,将数据保存到找到的第一个服务器上。如果超过232仍然找不到服务器,就会保存到第一台memcached服务器上。
容错性与可扩展性分析:在一致性哈希算法中,如果一台服务器不可用,则受影响的数据仅仅是此服务器到其环空间中前一台服务器(即顺着逆时针方向行走遇到的第一台服务器)之间数据,其它不会受到影响,在一致性哈希算法中,如果增加一台服务器,则受影响的数据仅仅是新服务器到其环空间中前一台服务器(即顺着逆时针方向行走遇到的第一台服务器)之间数据,其它不会受到影响。 一致性哈希算法在服务节点太少时,容易因为节点分部不均匀而造成数据倾斜问题。
代码实现:
import java.security.MessageDigest; import java.security.NoSuchAlgorithmException; import java.util.Collection; import java.util.SortedMap; import java.util.TreeMap; /** * 一致性Hash算法 * * @param <T> 节点类型 */ public class ConsistentHash<T> { /** * Hash计算对象,用于自定义hash算法 */ HashFunc hashFunc; /** * 复制的节点个数 */ private final int numberOfReplicas; /** * 一致性Hash环 */ private final SortedMap<Long, T> circle = new TreeMap<>(); /** * 构造,使用Java默认的Hash算法 * @param numberOfReplicas 复制的节点个数,增加每个节点的复制节点有利于负载均衡 * @param nodes 节点对象 */ public ConsistentHash(int numberOfReplicas, Collection<T> nodes) { this.numberOfReplicas = numberOfReplicas; this.hashFunc = new HashFunc() { @Override public Long hash(Object key) { // return fnv1HashingAlg(key.toString()); return md5HashingAlg(key.toString()); } }; //初始化节点 for (T node : nodes) { add(node); } } /** * 构造 * @param hashFunc hash算法对象 * @param numberOfReplicas 复制的节点个数,增加每个节点的复制节点有利于负载均衡 * @param nodes 节点对象 */ public ConsistentHash(HashFunc hashFunc, int numberOfReplicas, Collection<T> nodes) { this.numberOfReplicas = numberOfReplicas; this.hashFunc = hashFunc; //初始化节点 for (T node : nodes) { add(node); } } /** * 增加节点<br> * 每增加一个节点,就会在闭环上增加给定复制节点数<br> * 例如复制节点数是2,则每调用此方法一次,增加两个虚拟节点,这两个节点指向同一Node * 由于hash算法会调用node的toString方法,故按照toString去重 * * @param node 节点对象 */ public void add(T node) { for (int i = 0; i < numberOfReplicas; i++) { circle.put(hashFunc.hash(node.toString() + i), node); } } /** * 移除节点的同时移除相应的虚拟节点 * * @param node 节点对象 */ public void remove(T node) { for (int i = 0; i < numberOfReplicas; i++) { circle.remove(hashFunc.hash(node.toString() + i)); } } /** * 获得一个最近的顺时针节点 * * @param key 为给定键取Hash,取得顺时针方向上最近的一个虚拟节点对应的实际节点 * @return 节点对象 */ public T get(Object key) { if (circle.isEmpty()) { return null; } long hash = hashFunc.hash(key); if (!circle.containsKey(hash)) { SortedMap<Long, T> tailMap = circle.tailMap(hash); //返回此映射的部分视图,其键大于等于 hash hash = tailMap.isEmpty() ? circle.firstKey() : tailMap.firstKey(); } //正好命中 return circle.get(hash); } /** * 使用MD5算法 * @param key * @return */ private static long md5HashingAlg(String key) { MessageDigest md5 = null; try { md5 = MessageDigest.getInstance("MD5"); md5.reset(); md5.update(key.getBytes()); byte[] bKey = md5.digest(); long res = ((long) (bKey[3] & 0xFF) << 24) | ((long) (bKey[2] & 0xFF) << 16) | ((long) (bKey[1] & 0xFF) << 8)| (long) (bKey[0] & 0xFF); return res; } catch (NoSuchAlgorithmException e) { e.printStackTrace(); } return 0l; } /** * 使用FNV1hash算法 * @param key * @return */ private static long fnv1HashingAlg(String key) { final int p = 16777619; int hash = (int) 2166136261L; for (int i = 0; i < key.length(); i++) hash = (hash ^ key.charAt(i)) * p; hash += hash << 13; hash ^= hash >> 7; hash += hash << 3; hash ^= hash >> 17; hash += hash << 5; return hash; } /** * Hash算法对象,用于自定义hash算法 */ public interface HashFunc { public Long hash(Object key); } }
8. 死锁的四个必要条件,避免方法?
4个必要条件:
(1)互斥条件:进程对所分配到的资源不允许其他进程进行访问,若其他进程访问该资源,只能等待,直至占有该资源的进程使用完成后释放该资源
(2)请求和保持条件:进程获得一定的资源之后,又对其他资源发出请求,但是该资源可能被其他进程占有,此事请求阻塞,但又对自己获得的资源保持不放
(3)不可剥夺条件:是指进程已获得的资源,在未完成使用之前,不可被剥夺,只能在使用完后自己释放
(4)环路等待条件:是指进程发生死锁后,必然存在一个进程--资源之间的环形链
处理方法:
(1).预防死锁:通过设置一些限制条件,去破坏产生死锁的必要条件
(2).避免死锁:在资源分配过程中,使用某种方法避免系统进入不安全的状态,从而避免发生死锁
(3).检测死锁:允许死锁的发生,但是通过系统的检测之后,采取一些措施,将死锁清除掉
(4).解除死锁:该方法与检测死锁配合使用
9. HTTP常见响应码:200、301、302、404、500?
200 (成功) 服务器已成功处理了请求。 通常,这表示服务器提供了请求的网页。
301 (永久移动) 请求的网页已永久移动到新位置。 服务器返回此响应(对 GET 或 HEAD 请求的响应)时,会自动将请求者转到新位置。
302 (临时移动) 服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求。
404 (未找到) 服务器找不到请求的网页。
500 (服务器内部错误) 服务器遇到错误,无法完成请求。
10. get和post的区别?
get参数通过url传递,post放在request body中。
get请求在url中传递的参数是有长度限制的,而post没有。
get比post更不安全,因为参数直接暴露在url中,所以不能用来传递敏感信息。
get请求只能进行url编码,而post支持多种编码方式
get请求会浏览器主动cache,而post支持多种编码方式。
get请求参数会被完整保留在浏览历史记录里,而post中的参数不会被保留。
GET和POST本质上就是TCP链接,并无差别。但是由于HTTP的规定和浏览器/服务器的限制,导致他们在应用过程中体现出一些不同。
GET产生一个TCP数据包;POST产生两个TCP数据包。
长的说:
对于GET方式的请求,浏览器会把http header和data一并发送出去,服务器响应200(返回数据);
而对于POST,浏览器先发送header,服务器响应100 continue,浏览器再发送data,服务器响应200 ok(返回数据)。
11. 内连接、左连接、右连接的作用及区别?
左连接:左边有的,右边没有的为null
右连接:左边没有的,右边有的为null
内连接:显示左边右边共有的
12. 面向对象的三大基本特征,五大基本原则 ?
三大特性是:封装,继承,多态
五大基本原则 :单一职责原则SRP、开放封闭原则OCP、替换原则LSP、依赖原则DIP、接口分离原则ISP
13. Collection 和 Collections的区别?
1、java.util.Collection 是一个集合接口(集合类的一个顶级接口)。它提供了对集合对象进行基本操作的通用接口方法。Collection接口在Java 类库中有很多具体的实现。Collection接口的意义是为各种具体的集合提供了最大化的统一操作方式,其直接继承接口有List与Set
Collection
├List
│├LinkedList
│├ArrayList
│└Vector
│ └Stack
└Set
2、Collections则是集合类的一个工具类/帮助类,其中提供了一系列静态方法,用于对集合中元素进行排序、搜索以及线程安全等各种操作。




