树状树组

这里丢一篇很好的blogs

https://www.cnblogs.com/hsd-/p/6139376.html

其实树状数组的是实现是根据二进制的

主要的函数有这三个

int lowbit(int x)
{
    return x&(-x);
}

这个是返回原数上去除末尾一个1的数

such as 

1. t=6（0110）
2. -t=-6=(1001+1)=(1010)
3. t&(-t)=(0010)=2 得到这个有什么用呢，继续看

    现在定义每一列的顶端结点C[]数组 

   如下图

 

 

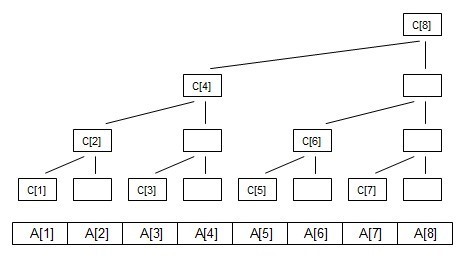
   C[i]代表 子树的叶子结点的权值之和// 这里以求和举例

   如图可以知道

   C[1]=A[1];

   C[2]=A[1]+A[2];

   C[3]=A[3];

   C[4]=A[1]+A[2]+A[3]+A[4];

   C[5]=A[5];

   C[6]=A[5]+A[6];

   C[7]=A[7];

   C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

将C[]数组的结点序号转化为二进制

1=(001)      C[1]=A[1];

2=(010)      C[2]=A[1]+A[2];

3=(011)      C[3]=A[3];

4=(100)      C[4]=A[1]+A[2]+A[3]+A[4];

5=(101)      C[5]=A[5];

6=(110)      C[6]=A[5]+A[6];

7=(111)      C[7]=A[7];

8=(1000)    C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

对照式子可以发现  C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k为i的二进制中从最低位到高位连续零的长度）例如i=8时，k=3; 

举个例子 i=7;

sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ;   //前i项和

C[4]=A[1]+A[2]+A[3]+A[4];   C[6]=A[5]+A[6];   C[7]=A[7];

可以推出:   sum[7]=C[4]+C[6]+C[7];

序号写为二进制: sum[(111)]=C[(100)]+C[(110)]+C[(111)];

 

再举个例子 i=5

sum[7]=A[1]+A[2]+A[3]+A[4]+A[5] ;   前i项和

C[4]=A[1]+A[2]+A[3]+A[4];   C[5]=A[5];

可以推出:   sum[5]=C[4]+C[5];

序号写为二进制: sum[(101)]=C[(100)]+C[(101)];

所以说我们可以通过对i加减lowbit(i),就能实现得到111 110 100 000这样的数

int add(int i,int x)
{
    while (i<=n)
    {
        c[i]+=x;
        i+=lowbit(i);
    }
}

这个呢是树状数组实现单点修改

int sum(int i)
{
    int res=0;
    while (i>=1)
    {
        res+=c[i];
        i-=lowbit(i);
    }
    return res;
}

这个是实现区间求和查询跟上面的是一样的意识

 

 

 

1.树状数组求逆序对

#include<iostream>
#include<algorithm>
using namespace std;
struct sb
{
    int z,num;
}t[1001];
int c[1001],n;
bool cmp(sb a,sb b)
{
    return a.z<b.z?true:false;
}
int lowbit(int x)
{
    return x&(-x);
}
int add(int i,int x)
{
    while (i<=n)
    {
        c[i]+=x;
        i+=lowbit(i);
    }
}
int sum(int i)
{
    int res=0;
    while (i>=1)
    {
        res+=c[i];
        i-=lowbit(i);
    }
    return res;
}
int main ()
{
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        cin>>t[i].z;
        t[i].num=i;
    }
    sort(t+1,t+1+n,cmp);
    int ans=0;
    for (int i=1;i<=n;i++)
    {
        add(t[i].num,1);
        ans+=i-sum(t[i].num);
    }
    cout<<ans;
} 

2.树状数组优化最长上升下降序列

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int a[100001];
struct sb
{
    int num,val;
}b[100001];
int n,t[100001*4];
bool cmp (sb a,sb b) { return a.val<b.val?true:false; }
int lowbit(int x) { return x&(-x); }
void add(int i,int k)
{
    while (i<=n)
    {
        t[i]=max(t[i],k);
        i+=lowbit(i);
    }
 } 
int find(int i)
{
    int ans=-1e9;
    while (i)
    {
        ans=max(ans,t[i]);
        i-=lowbit(i);
    }
    return ans;
}
int main ()
{
    int ans=0;
    cin>>n;
    for (int i=1;i<=n;i++) scanf("%d",&a[i]);
    for (int j=1;j<=n;j++) scanf("%d",&b[j].val),b[j].num=j;
    sort(b+1,b+1+n,cmp);
    for (int i=1;i<=n;i++) a[i]=b[a[i]].num;
    for (int i=n;i>=1;i--)
    {
        int nt=find(a[i]);
        add(a[i],++nt);
        ans=max(nt,ans);
    }
    cout<<ans;
}

 　树状树，区间修改单点查询，差分数组

#include<iostream>
using namespace std;
int a[500001],b[500001],t[1000000];
int n,m;
int lowbit(int x){return x&(-x);}
void add(int i,int k){for (i;i<=n;i+=lowbit(i)) t[i]+=k;}
int get(int i,int ans){for (i;i;i-=lowbit(i)) ans+=t[i]; return ans;}
int main ()
{
    cin>>n>>m;
    for (int i=1;i<=n;i++)
       cin>>a[i],b[i]=a[i]-a[i-1],add(i,b[i]);
    for (int i=1,op,x,y,z;i<=m;i++)
    {
        cin>>op;
        if (op==1)
        {
            cin>>x>>y>>z;
            add(x,z);
            add(y+1,-z); 
        }
        else
        {
            cin>>x;
            cout<<get(x,0)<<endl; 
        }
    } 
    
}