数据结构名词简述
数据结构的存储方式只有两种:数组(顺序存储)和链表(链式存储)
其它的数据结构都是都是在链表或者数组上的特殊操作。
队列、栈
既可以使用数组,也可以使用链表实现。用数组实现,考虑扩容缩容的问题;用链表实现,需要更多的内存空间。
图
分为有向图和无向图。表示的方法有:邻接表(链表)和邻接矩阵(数组)。
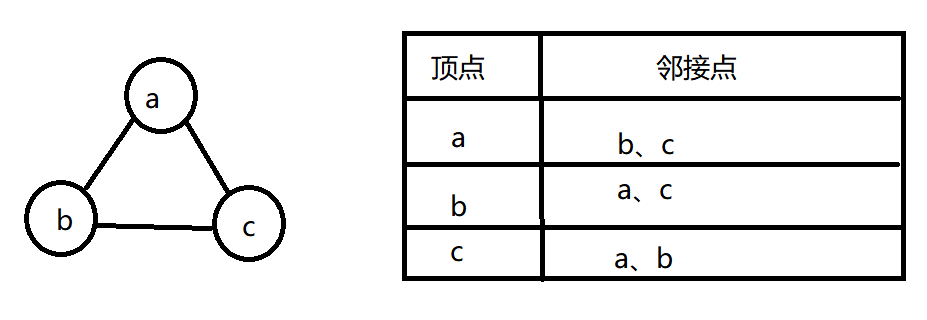
邻接表:把每个顶点和其相邻的顶点用表格列出来。节省空间,但是操作效率上不如邻接矩阵。
邻接矩阵:二维数组,布尔矩阵。判断连通性迅速,并可以使用矩阵运算解决一些问题,但是图比较稀疏的话很耗费空间。
散列表
Hash Table是根据键(key)而直接访问在内存存储位置的数据结构。通过散列函数,将所需查找的数据映射到表中一个位置来访问记录,没有哈希冲突的时候,时间复杂度是O(1)。
为什么哈希表的查找速度非常快?
因为哈希函数建立了键和存储位置的映射:存储位置 = f(key)
在查找一个元素的时候,不需要像数组一样逐个遍历比对,只需要用哈希函数计算一下关键字的hash值,即可直接找到它的存储位置。
哈希冲突:key1 != key2,但是f(key1) = f(key2)
解决冲突的方法:
- 拉链法:数组 + 链表
- 线性探测法:查找散列表中离冲突单元最近的空闲单元,并且把新的键插入这个空闲单元
拉链法
| 存储方法 | 优点 | 缺点 |
|---|---|---|
| 数组(顺序存储) | 随机读取效率很高 | 不适合大量数据的插入删除 |
| 链表(链式存储) | 查找效率低 | 数据的插入删除很容易 |
拉链法结合了数组和链表的优点,处理冲突简单,且无堆积现象。
线性探测法
开放定址法的一种。
容易产生堆积问题;不适于大规模的数据存储;散列函数的设计对冲突会有很大的影响;插入时可能会出现多次冲突的现象,删除的元素是多个冲突元素中的一个,需要对后面的元素作处理,实现较复杂;结点规模很大时会浪费很多空间
树
堆可以被看作是一棵(每层结点都完全填满,在最后一层上如果不是满的,则只缺少右边的若干结点。)的数组对象,也被称为优先队列,在堆底插入元素,在堆顶取出元素,堆中元素是按照一定的优先顺序排列的。



