(多校)校门外歪脖树上的鸽子 (pigeons)
先观察题目性质
考虑形式化满足哪些条件的点被选( update / query )
我们观察一张图:
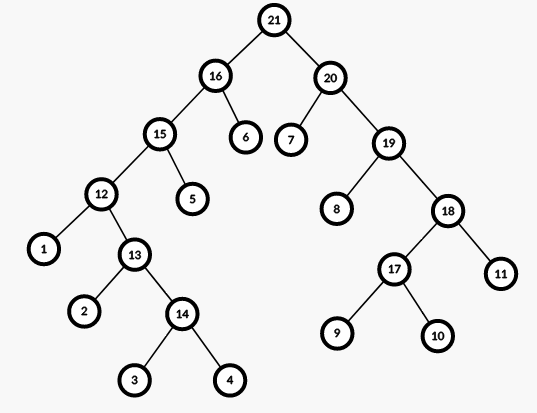
对于上图区间 \([3,10]\),选的的点依次为:\(14,5,6,7,8,17\)
其实就是我们把 \(l~r\) 点的树上路径拿下来
根据 \(lca\) 把树分为两部分
我们把左链和右链分开考虑
对于左链:
先对于节点 \(l\) ,我们找到 \(l\) 一直向右上跳的最远位置(设其为 \(a\))
如果这个点不是 \(lca\) 【 我们需要对于是否会直接跳到 \(lca\) 分开考虑 】
那 \(a\) 就是其中一个被选点
对于 \(fa[a] - lca\) 这条链如果某节点为左儿子
那么他的兄弟节点就为被选点
( 右链反之 ) ( 询问与更改对应 )
Code
#include <bits/stdc++.h>
#define re register
#define int long long
// #define ll long long
// #define lls long long
#define pir make_pair
#define fr first
#define sc second
#define db double
using namespace std;
const int mol=993244853;
const int maxn=5e5+10;
const int INF=1e9+10;
inline int qpow(int a,int b) { int ans=1; while(b) { if(b&1) (ans*=a)%=mol; (a*=a)%=mol; b>>=1; } return (ans+mol)%mol; }
inline int read() {
int s=0,w=1; char ch=getchar();
while(ch<'0'||ch>'9') { if(ch=='-') w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9') { s=s*10+ch-'0'; ch=getchar(); }
return s*w;
}
int n,m,root,w[maxn]; bool isl[maxn],isr[maxn]; int backl[maxn],backr[maxn],bro[maxn];
struct DATE { int l,r,ll,rr; } dat[maxn];
struct STG {
#define lid (id<<1)
#define rid (id<<1|1)
struct TREE { int sum,ks,lazy; } tre[maxn<<2]; int w[maxn];
inline void build(int id,int l,int r) {
if(l==r) { tre[id].ks=w[l]; return ; }
int mid=(l+r)>>1;
build(lid,l,mid); build(rid,mid+1,r);
tre[id].ks=tre[lid].ks+tre[rid].ks;
}
inline void push_down(int id) {
int s=tre[id].lazy; tre[id].lazy=0;
tre[lid].lazy+=s; tre[rid].lazy+=s;
tre[lid].sum+=tre[lid].ks*s; tre[rid].sum+=tre[rid].ks*s;
}
inline void ins(int id,int l,int r,int ll,int rr,int val) {
if(ll<=l&&r<=rr) { tre[id].lazy+=val; tre[id].sum+=val*tre[id].ks; return ; }
if(tre[id].lazy) push_down(id);
int mid=(l+r)>>1;
if(ll<=mid) ins(lid,l,mid,ll,rr,val);
if(rr>mid) ins(rid,mid+1,r,ll,rr,val);
tre[id].sum=tre[lid].sum+tre[rid].sum;
}
inline int quy(int id,int l,int r,int ll,int rr) {
if(ll<=l&&r<=rr) { return tre[id].sum; }
if(tre[id].lazy) push_down(id);
int mid=(l+r)>>1,ans=0;
if(ll<=mid) ans+=quy(lid,l,mid,ll,rr);
if(rr>mid) ans+=quy(rid,mid+1,r,ll,rr);
return ans;
}
} trel,trer;
int size[maxn],son[maxn],dep[maxn],fa[maxn];
int tot,dfn[maxn],top[maxn],eid[maxn];
inline void dfs1(int now) {
size[now]=1; dep[now]=dep[fa[now]]+1;
if(!backl[now]) backl[now]=now;
if(!backr[now]) backr[now]=now;
if(!dat[now].l&&!dat[now].r) { dat[now].ll=dat[now].rr=now; return ; }
backr[dat[now].l]=backr[now]; dfs1(dat[now].l); size[now]+=size[dat[now].l];
backl[dat[now].r]=backl[now]; dfs1(dat[now].r); size[now]+=size[dat[now].r];
son[now]=size[dat[now].l]>size[dat[now].r]? dat[now].l:dat[now].r;
w[dat[now].l]=(dat[dat[now].r].rr-dat[dat[now].r].ll+1);
w[dat[now].r]=(dat[dat[now].l].rr-dat[dat[now].l].ll+1);
dat[now].ll=dat[dat[now].l].ll;
dat[now].rr=dat[dat[now].r].rr;
}
inline void dfs2(int now,int pre) {
dfn[now]=++tot; eid[tot]=now; top[now]=pre;
if(son[now]) dfs2(son[now],pre); else return ;
if(dat[now].l!=son[now]) {
dfs2(dat[now].l,dat[now].l);
}
if(dat[now].r!=son[now]) {
dfs2(dat[now].r,dat[now].r);
}
}
inline int getlca(int a,int b) {
while(top[a]!=top[b]) {
if(dep[top[a]]<dep[top[b]]) swap(a,b);
a=fa[top[a]];
}
return dep[a]<dep[b]? a:b;
}
inline void wor(int a,int b,int d) {
int lca=getlca(a,b);
if(dep[backr[a]]<=dep[lca]&&dep[backl[b]]<=dep[lca]) {
if(lca==root) w[lca]+=(dat[lca].rr-dat[lca].ll+1)*d;
else if(isl[lca]) { trer.ins(1,1,tot,dfn[bro[lca]],dfn[bro[lca]],d); }
else if(isr[lca]) { trel.ins(1,1,tot,dfn[bro[lca]],dfn[bro[lca]],d); }
return ;
}
if(dep[backr[a]]<=dep[lca]) {
a=dat[lca].l;
if(isl[a]) { trer.ins(1,1,tot,dfn[bro[a]],dfn[bro[a]],d); }
else if(isr[a]) { trel.ins(1,1,tot,dfn[bro[a]],dfn[bro[a]],d); }
} else {
a=backr[a];
if(isl[a]) { trer.ins(1,1,tot,dfn[bro[a]],dfn[bro[a]],d); }
else if(isr[a]) { trel.ins(1,1,tot,dfn[bro[a]],dfn[bro[a]],d); }
a=fa[a]; int lim=dat[lca].l;
if(dep[a]>dep[lim]) {
while(dep[top[a]]>dep[lim]) {
trel.ins(1,1,tot,dfn[top[a]],dfn[a],d); a=fa[top[a]];
}
if(dep[a]>dep[lim]) {
int ls=top[dat[lim].l]==top[a]? dat[lim].l:dat[lim].r;
trel.ins(1,1,tot,dfn[ls],dfn[a],d);
}
}
}
if(dep[backl[b]]<=dep[lca]) {
b=dat[lca].r;
if(isl[b]) { trer.ins(1,1,tot,dfn[bro[b]],dfn[bro[b]],d); }
else if(isr[b]) { trel.ins(1,1,tot,dfn[bro[b]],dfn[bro[b]],d); }
} else {
b=backl[b];
if(isl[b]) { trer.ins(1,1,tot,dfn[bro[b]],dfn[bro[b]],d); }
else if(isr[b]) { trel.ins(1,1,tot,dfn[bro[b]],dfn[bro[b]],d); }
b=fa[b]; int lim=dat[lca].r;
if(dep[b]>dep[lim]) {
while(dep[top[b]]>dep[lim]) {
trer.ins(1,1,tot,dfn[top[b]],dfn[b],d); b=fa[top[b]];
}
if(dep[b]>dep[lim]) {
int ls=top[dat[lim].l]==top[b]? dat[lim].l:dat[lim].r;
trer.ins(1,1,tot,dfn[ls],dfn[b],d);
}
}
}
}
inline int qus(int a,int b) {
int lca=getlca(a,b),ans=0;
if(dep[backr[a]]<=dep[lca]&&dep[backl[b]]<=dep[lca]) {
if(lca==root) ans+=w[lca];
else if(isl[lca]) { ans+=trer.quy(1,1,tot,dfn[bro[lca]],dfn[bro[lca]]); }
else if(isr[lca]) { ans+=trel.quy(1,1,tot,dfn[bro[lca]],dfn[bro[lca]]); }
return ans;
}
if(dep[backr[a]]<=dep[lca]) {
a=dat[lca].l;
if(isl[a]) { ans+=trer.quy(1,1,tot,dfn[bro[a]],dfn[bro[a]]); }
else if(isr[a]) { ans+=trel.quy(1,1,tot,dfn[bro[a]],dfn[bro[a]]); }
} else {
a=backr[a];
if(isl[a]) { ans+=trer.quy(1,1,tot,dfn[bro[a]],dfn[bro[a]]); }
else if(isr[a]) { ans+=trel.quy(1,1,tot,dfn[bro[a]],dfn[bro[a]]); }
a=fa[a]; int lim=dat[lca].l;
if(dep[a]>dep[lim]) {
while(dep[top[a]]>dep[lim]) {
ans+=trel.quy(1,1,tot,dfn[top[a]],dfn[a]); a=fa[top[a]];
}
if(dep[a]>dep[lim]) {
int ls=top[dat[lim].l]==top[a]? dat[lim].l:dat[lim].r;
ans+=trel.quy(1,1,tot,dfn[ls],dfn[a]);
}
}
}
if(dep[backl[b]]<=dep[lca]) {
b=dat[lca].r;
if(isl[b]) { ans+=trer.quy(1,1,tot,dfn[bro[b]],dfn[bro[b]]); }
else if(isr[b]) { ans+=trel.quy(1,1,tot,dfn[bro[b]],dfn[bro[b]]); }
} else {
b=backl[b];
if(isl[b]) { ans+=trer.quy(1,1,tot,dfn[bro[b]],dfn[bro[b]]); }
else if(isr[b]) { ans+=trel.quy(1,1,tot,dfn[bro[b]],dfn[bro[b]]); }
b=fa[b]; int lim=dat[lca].r;
if(dep[b]>dep[lim]) {
while(dep[top[b]]>dep[lim]) {
ans+=trer.quy(1,1,tot,dfn[top[b]],dfn[b]); b=fa[top[b]];
}
if(dep[b]>dep[lim]) {
int ls=top[dat[lim].l]==top[b]? dat[lim].l:dat[lim].r;
ans+=trer.quy(1,1,tot,dfn[ls],dfn[b]);
}
}
}
return ans;
}
signed main(void) {
freopen("pigeons.in","r",stdin); freopen("pigeons.out","w",stdout);
n=read(); m=read();
for(re int i=1,a,b;i<n;i++) {
dat[i+n].l=read(); dat[i+n].r=read();
bro[dat[i+n].l]=dat[i+n].r;
bro[dat[i+n].r]=dat[i+n].l;
fa[dat[i+n].l]=n+i; fa[dat[i+n].r]=n+i;
isl[dat[i+n].l]=1; isr[dat[i+n].r]=1;
}
for(re int i=n+1;i<2*n;i++) if(!fa[i]) { root=i; break; }
dfs1(root); dfs2(root,root);
for(re int i=1;i<2*n;i++) {
if(isl[i]) {
trel.w[dfn[i]]=w[i];
}
else if(isr[i]) {
trer.w[dfn[i]]=w[i];
}
}
trel.build(1,1,tot); trer.build(1,1,tot);
for(re int i=1,opt,l,r,d;i<=m;i++) {
opt=read();
if(opt==1) {
l=read(); r=read(); d=read();
wor(l,r,d);
}
else {
l=read(); r=read();
printf("%lld\n",qus(l,r));
}
}
return 0;
}


