家用热水器用户行为分析与事件识别
家用热水器用户行为分析与事件识别
依据BP神经网络算法构建洗浴事件识别模型,进而对不同地区的用户的洗浴事件进行识别,然后根据识别结果比较不同客户群的客户使用习惯,以加深对客户需求的理解等。从而厂商便可以对不同的客户群提供最适合的个性化产品,改进新产品的智能化研发并制定相应的营销策略。
目标
依据某热水器生产厂商提供的数据:
- 根据热水器采集到的数据,划分一次完整用水事件。
- 在划分好的一次完整用水事件中,识别出洗浴事件。
步骤
- 对热水器用户的历史用水数据进行选择性抽取,构建专家样本。
- 对步骤1形成的数据集,进行数据探索分析与预处理,包括探索水流量的分布情况,删除冗余属性,识别用水数据的缺失值,并对缺失值进行处理,然后根据建模的需要进行属性构造等。最后根据以上处理,对热水器用户用水样本数据建立用水事件时间间隔识别模型和划分一次完整的用水事件模型,接着在一次完整用水事件划分结果的基础上,剔除短暂用水事件、缩小识别范围等。
- 在步骤2得到的建模样本数据基础上,建立洗浴事件识别模型,对洗浴事件识别模型进行模型分析评价。
- 应用步骤3形成的模型结果,并对洗浴事件划分进行优化。
- 调用洗浴事件识别模型,对实时监控的热水器流水数据进行洗浴事件自动识别。
数据探索性分析
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline input_path = '../data/original_data.xls' data = pd.read_excel(input_path)
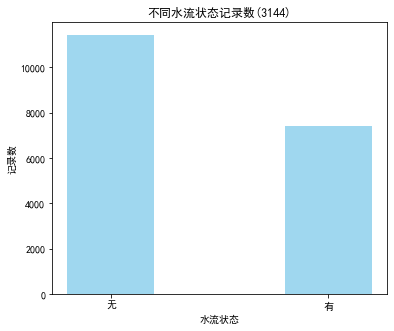
#查看有无水流的分布,绘制条形图 lv_non = pd.value_counts(data['有无水流'])['无'] lv_move= pd.value_counts(data['有无水流'])['有'] fig = plt.figure(figsize=(6,5)) plt.bar(range(2),height=[lv_non,lv_move],width=0.4,alpha=0.8,color='skyblue') plt.xticks([index for index in range(2)],['无','有']) plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号 plt.xlabel(u'水流状态') plt.ylabel(u'记录数') plt.title(u'不同水流状态记录数(3144)')
Text(0.5, 1.0, '不同水流状态记录数(3144)')
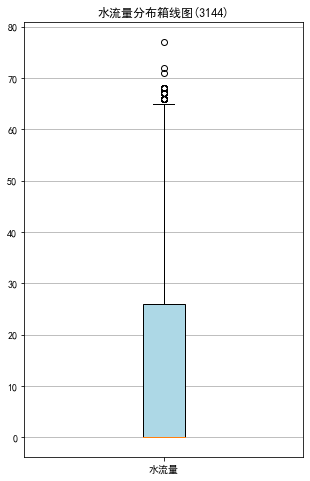
# 查看水流分布 water = data['水流量'] # 绘制水流量分布箱型图 fig = plt.figure(figsize=(5,8)) plt.boxplot(water,patch_artist=True, labels=['水流量'], boxprops={'facecolor':'lightblue'}) plt.title(u'水流量分布箱线图(3144)') plt.grid(axis='y')
data.shape
(18840, 12)
# 删除热水器编号、有无水流、节能模式属性 data.drop(labels=["热水器编号","有无水流","节能模式"],axis=1,inplace=True) print('删除冗余属性后的数据形状为:', data.shape) data.to_csv('../data/water_heart.csv',index=False)
删除冗余属性后的数据形状为: (18840, 9)
划分用水事件
“用水停顿时间间隔”定义为一条水流量不为0的流水记录同下一条水流量不为0的流水记录之间的时间间隔。
# 阈值为4分钟 threshold = pd.Timedelta('4 min') # 转换时间格式 data['发生时间'] = pd.to_datetime(data['发生时间'], format = '%Y%m%d%H%M%S') # 保留流量大于0的记录 data = data[data['水流量']>0] # 相邻时间向前差分,比较是否大于阈值 diff():df-df.shift() sjKs = data['发生时间'].diff() > threshold # 令第一个时间为第一个用水事件的开始事件 sjKs.iloc[0] = True sjJs = sjKs.iloc[1:] # 向后差分的结果 sjJs = pd.concat([sjJs,pd.Series(True)]) # 令最后一个时间作为最后一个用水事件的结束时间 # 创建数据框,并定义用水事件序列 sj = pd.DataFrame(np.arange(1,sum(sjKs)+1),columns = ["事件序号"]) sj["事件起始编号"] = data.index[sjKs == 1]+1 # 定义用水事件的起始编号 sj["事件终止编号"] = data.index[sjJs == 1]+1 # 定义用水事件的终止编号 print('当阈值为4分钟的时候事件数目为:',sj.shape[0]) sj.to_csv('../data/sj.csv',index = False)
当阈值为4分钟的时候事件数目为: 172
确定单次用水事件时长阈值
对某热水器用户的数据,根据不同的阈值划分用水事件,先统计出各个阈值下的用水事件的个数,再通过阈值寻优的方式找出最优的阈值。
阈值优化:
- 当存在一个阈值的斜率指标K<1时,则取阈值最小的点A(可能存在多个阈值的斜率指标小于1)的横坐标xA作为用水事件划分的阈值,其中K<1中的“1”是经过实际数据验证的一个专家阈值。
- 当不存在一个阈值的斜率指标K<1时,则找所有阈值中斜率指标最小的阈值;如果该阈值的斜率指标小于5,则取该阈值作为用水事件划分的阈值;如果该阈值的斜率指标不小于5,则阈值取默认值的阈值——4分钟。其中,“斜率指标小于5”中的“5”是经过实际数据验证的一个专家阈值。
# 使用以后四个点的平均斜率 n = 4 # 专家阈值 threshold = pd.Timedelta(minutes=5) data['发生时间'] = pd.to_datetime(data['发生时间'], format='%Y%m%d%H%M%S') data = data[data['水流量'] > 0] # 只要流量大于0的记录 #输入划分时间的时间阈值,得到划分的事件数 def event_num(ts): d = data['发生时间'].diff()>ts return d.sum()+1 dt = [pd.Timedelta(minutes=i) for i in np.arange(1,9,0.25)] h = pd.DataFrame(dt,columns=['阈值']) # 计算每个阈值对应的事件数 h['事件数'] = h['阈值'].apply(event_num) # 计算每两个相邻点对应的斜率 h['斜率'] = h['事件数'].diff()/0.25 # 往前取n个斜率绝对值平均作为斜率指标 h['斜率指标']= h['斜率'].abs().rolling(4).mean() # 用idxmin返回最小值的Index,由于rolling_mean()计算的是前n个斜率的绝对值平均,所以结果要进行平移(-n) ts = h['阈值'][h['斜率指标'].idxmin()-n] if ts > threshold: ts = pd.Timedelta(minutes=4) print('计算出的单次用水时长的阈值为:',ts)
计算出的单次用水时长的阈值为: 0 days 00:04:00
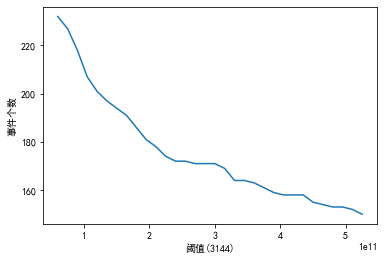
图中某段阈值范围内,下降趋势明显,说明在该段阈值范围内,热水器用户的停顿习惯比较集中。如果趋势比较平缓,则说明热水器用户停顿热水的习惯趋于稳定,所以取该段时间开始的时间点作为阈值,既不会将短的用水事件合并,又不会将长的用水事件拆开
plt.plot(h['阈值'],h['事件数']) plt.xlabel(u'阈值') plt.ylabel(u'事件个数')
Text(0, 0.5, '事件个数')
属性构造
data = pd.read_csv('../data/water_heart.csv') # 读取用水事件记录 sj = pd.read_csv('../data/sj.csv') # 转换时间格式 data["发生时间"] = pd.to_datetime(data["发生时间"],format="%Y%m%d%H%M%S") # 构造特征:总用水时长 timeDel = pd.Timedelta("0.5 sec") sj["事件开始时间"] = data.iloc[sj["事件起始编号"]-1,0].values- timeDel sj["事件结束时间"] = data.iloc[sj["事件终止编号"]-1,0].values + timeDel sj['洗浴时间点'] = [i.hour for i in sj["事件开始时间"]] sj["总用水时长"] = np.int64(sj["事件结束时间"] - sj["事件开始时间"])/1000000000 + 1 # 构造用水停顿事件 # 构造特征“停顿开始时间”、“停顿结束时间” # 停顿开始时间指从有水流到无水流,停顿结束时间指从无水流到有水流 for i in range(len(data)-1): if (data.loc[i,"水流量"] != 0) & (data.loc[i + 1,"水流量"] == 0) : data.loc[i + 1,"停顿开始时间"] = data.loc[i +1, "发生时间"] - timeDel if (data.loc[i,"水流量"] == 0) & (data.loc[i + 1,"水流量"] != 0) : data.loc[i,"停顿结束时间"] = data.loc[i , "发生时间"] + timeDel # 提取停顿开始时间与结束时间所对应行号,放在数据框Stop中 indStopStart = data.index[data["停顿开始时间"].notnull()]+1 indStopEnd = data.index[data["停顿结束时间"].notnull()]+1 Stop = pd.DataFrame(data={"停顿开始编号":indStopStart[:-1], "停顿结束编号":indStopEnd[1:]}) # 计算停顿时长,并放在数据框stop中,停顿时长=停顿结束时间-停顿结束时间 Stop["停顿时长"] = np.int64(data.loc[indStopEnd[1:]-1,"停顿结束时间"].values- data.loc[indStopStart[:-1]-1,"停顿开始时间"].values)/1000000000 # 将每次停顿与事件匹配,停顿的开始时间要大于事件的开始时间, # 且停顿的结束时间要小于事件的结束时间 for i in range(len(sj)): Stop.loc[(Stop["停顿开始编号"] > sj.loc[i,"事件起始编号"]) & (Stop["停顿结束编号"] < sj.loc[i,"事件终止编号"]),"停顿归属事件"]=i+1 # 删除停顿次数为0的事件 Stop = Stop[Stop["停顿归属事件"].notnull()] # 构造特征 用水事件停顿总时长、停顿次数、停顿平均时长、 # 用水时长,用水/总时长 stopAgg = Stop.groupby("停顿归属事件").agg({"停顿时长":sum,"停顿开始编号":len}) sj.loc[stopAgg.index - 1,"总停顿时长"] = stopAgg.loc[:,"停顿时长"].values sj.loc[stopAgg.index-1,"停顿次数"] = stopAgg.loc[:,"停顿开始编号"].values sj.fillna(0,inplace=True) # 对缺失值用0插补 stopNo0 = sj["停顿次数"] != 0 # 判断用水事件是否存在停顿 sj.loc[stopNo0,"平均停顿时长"] = sj.loc[stopNo0,"总停顿时长"]/sj.loc[stopNo0,"停顿次数"] sj.fillna(0,inplace=True) # 对缺失值用0插补 sj["用水时长"] = sj["总用水时长"] - sj["总停顿时长"] # 定义特征用水时长 sj["用水/总时长"] = sj["用水时长"] / sj["总用水时长"] # 定义特征 用水/总时长 print('用水事件用水时长与频率特征构造完成后数据的特征为:\n',sj.columns) print('用水事件用水时长与频率特征构造完成后数据的前5行5列特征为:\n', sj.iloc[:5,:5])
用水事件用水时长与频率特征构造完成后数据的特征为:
Index(['事件序号', '事件起始编号', '事件终止编号', '事件开始时间', '事件结束时间', '洗浴时间点', '总用水时长',
'总停顿时长', '停顿次数', '平均停顿时长', '用水时长', '用水/总时长'],
dtype='object')
用水事件用水时长与频率特征构造完成后数据的前5行5列特征为:
事件序号 事件起始编号 事件终止编号 事件开始时间 事件结束时间
0 1 3 3 2014-10-19 07:01:55.500 2014-10-19 07:01:56.500
1 2 57 57 2014-10-19 07:38:15.500 2014-10-19 07:38:16.500
2 3 382 385 2014-10-19 09:46:37.500 2014-10-19 09:47:15.500
3 4 405 405 2014-10-19 11:50:16.500 2014-10-19 11:50:17.500
4 5 408 408 2014-10-19 13:56:20.500 2014-10-19 13:56:21.500
data["水流量"] = data["水流量"] / 60 # 原单位L/min,现转换为L/sec sj["总用水量"] = 0 # 给总用水量赋一个初始值0 for i in range(len(sj)): Start = sj.loc[i,"事件起始编号"]-1 End = sj.loc[i,"事件终止编号"]-1 if Start != End: for j in range(Start,End): if data.loc[j,"水流量"] != 0: sj.loc[i,"总用水量"] = (data.loc[j + 1,"发生时间"] - data.loc[j,"发生时间"]).seconds* \ data.loc[j,"水流量"] + sj.loc[i,"总用水量"] sj.loc[i,"总用水量"] = sj.loc[i,"总用水量"] + data.loc[End,"水流量"] * 2 else: sj.loc[i,"总用水量"] = data.loc[Start,"水流量"] * 2 sj["平均水流量"] = sj["总用水量"] / sj["用水时长"] # 定义特征 平均水流量 # 构造特征:水流量波动 # 水流量波动=∑(((单次水流的值-平均水流量)^2)*持续时间)/用水时长 sj["水流量波动"] = 0 # 给水流量波动赋一个初始值0 for i in range(len(sj)): Start = sj.loc[i,"事件起始编号"] - 1 End = sj.loc[i,"事件终止编号"] - 1 for j in range(Start,End + 1): if data.loc[j,"水流量"] != 0: slbd = (data.loc[j,"水流量"] - sj.loc[i,"平均水流量"])**2 slsj = (data.loc[j + 1,"发生时间"] - data.loc[j,"发生时间"]).seconds sj.loc[i,"水流量波动"] = slbd * slsj + sj.loc[i,"水流量波动"] sj.loc[i,"水流量波动"] = sj.loc[i,"水流量波动"] / sj.loc[i,"用水时长"] # 构造特征:停顿时长波动 # 停顿时长波动=∑(((单次停顿时长-平均停顿时长)^2)*持续时间)/总停顿时长 sj["停顿时长波动"] = 0 # 给停顿时长波动赋一个初始值0 for i in range(len(sj)): if sj.loc[i,"停顿次数"] > 1: # 当停顿次数为0或1时,停顿时长波动值为0,故排除 for j in Stop.loc[Stop["停顿归属事件"] == (i+1),"停顿时长"].values: sj.loc[i,"停顿时长波动"] = ((j - sj.loc[i,"平均停顿时长"])**2) * j + \ sj.loc[i,"停顿时长波动"] sj.loc[i,"停顿时长波动"] = sj.loc[i,"停顿时长波动"] / sj.loc[i,"总停顿时长"] print('用水量和波动特征构造完成后数据的特征为:\n',sj.columns) print('用水量和波动特征构造完成后数据的前5行5列特征为:\n',sj.iloc[:5,:5])
用水量和波动特征构造完成后数据的特征为:
Index(['事件序号', '事件起始编号', '事件终止编号', '事件开始时间', '事件结束时间', '洗浴时间点', '总用水时长',
'总停顿时长', '停顿次数', '平均停顿时长', '用水时长', '用水/总时长', '总用水量', '平均水流量', '水流量波动',
'停顿时长波动'],
dtype='object')
用水量和波动特征构造完成后数据的前5行5列特征为:
事件序号 事件起始编号 事件终止编号 事件开始时间 事件结束时间
0 1 3 3 2014-10-19 07:01:55.500 2014-10-19 07:01:56.500
1 2 57 57 2014-10-19 07:38:15.500 2014-10-19 07:38:16.500
2 3 382 385 2014-10-19 09:46:37.500 2014-10-19 09:47:15.500
3 4 405 405 2014-10-19 11:50:16.500 2014-10-19 11:50:17.500
4 5 408 408 2014-10-19 13:56:20.500 2014-10-19 13:56:21.500
sj_bool = (sj['用水时长'] >100) & (sj['总用水时长'] > 120) & (sj['总用水量'] > 5) sj_final = sj.loc[sj_bool,:] sj_final.to_csv('./sj_final.csv',index=False) print('筛选出候选洗浴事件前的数据形状为:',sj.shape) print('筛选出候选洗浴事件后的数据形状为:',sj_final.shape)
筛选出候选洗浴事件前的数据形状为: (172, 16) 筛选出候选洗浴事件后的数据形状为: (75, 16)
模型训练
import pandas as pd from sklearn.preprocessing import StandardScaler from sklearn.neural_network import MLPClassifier import joblib # 读取数据 Xtrain = pd.read_csv('../data/sj_final.csv') ytrain = pd.read_excel('../data/water_heater_log.xlsx') test = pd.read_excel('../data/test_data.xlsx') # 训练集测试集区分 x_train, x_test, y_train, y_test = Xtrain.iloc[:,5:],test.iloc[:,4:-1],\ ytrain.iloc[:,-1],test.iloc[:,-1] # 标准化 stdScaler = StandardScaler().fit(x_train) x_stdtrain = stdScaler.transform(x_train) x_stdtest = stdScaler.transform(x_test) # 建立模型 bpnn = MLPClassifier(hidden_layer_sizes = (17,10), max_iter = 200, solver = 'lbfgs',random_state=50) bpnn.fit(x_stdtrain, y_train) # 保存模型 joblib.dump(bpnn,'../data/water_heater_nnet.m') print('构建的模型为:\n',bpnn)
构建的模型为: MLPClassifier(hidden_layer_sizes=(17, 10), random_state=50, solver='lbfgs')
模型评估
# 模型评价 from sklearn.metrics import classification_report from sklearn.metrics import roc_curve import joblib import matplotlib.pyplot as plt bpnn = joblib.load('../data/water_heater_nnet.m') # 加载模型 y_pred = bpnn.predict(x_stdtest) # 返回预测结果 print('神经网络预测结果评价报告:\n',classification_report(y_test,y_pred)) # 绘制roc曲线图 fpr, tpr, thresholds = roc_curve(y_pred,y_test) # 求出TPR和FPR plt.figure(figsize=(6,4)) # 创建画布 plt.plot(fpr,tpr) # 绘制曲线 plt.title('用户用水事件识别ROC曲线(3144)') # 标题 plt.xlabel('FPR') # x轴标签 plt.ylabel('TPR') # y轴标签 plt.savefig('../data/ROC.png') # 保存图片
神经网络预测结果评价报告:
precision recall f1-score support
0 0.47 0.75 0.58 12
1 0.90 0.73 0.81 37
accuracy 0.73 49
macro avg 0.69 0.74 0.69 49
weighted avg 0.80 0.73 0.75 49

从上述结果可以看出,在洗浴事件的识别上精确率非常高,达到了90%,同时召回率也达到了70%以上。综合上述结果,可以确定此次创建的模型是有效且效果良好,能够用于实际的洗浴事件的识别中。






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本