商品零售购物篮分析
目标
通过对商场销售数据进行分析,得到顾客的购买行为特征,并根据发现的规律而采取有效的行动,制定商品摆放、商品定价、新商品采购计划,对增加销量并获取最大利润有重要意义。请根据提供的数据实现以下目标:
- 构建零售商品的Apriori关联规则模型,分析商品之间的关联性。
- 根据模型结果给出销售策略。
分析方法
购物篮关联规则挖掘的主要步骤如下:
- 对原始数据进行数据探索性分析,分析商品的热销情况与商品结构。
- 对原始数据进行数据预处理,转换数据形式,使之符合Apriori关联规则算法要求。
- 在步骤2得到的建模数据基础上,采用Apriori关联规则算法调整模型输入参数,完成商品关联性分析。
- 结合实际业务,对模型结果进行分析,根据分析结果给出销售建议,最后输出关联规则结果。
数据探索分析
查看数据特征以及对商品热销情况和商品结构进行分析
1. 数据特征
import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline inputfile = '../data/GoodsOrder.csv' # 输入的数据文件 data = pd.read_csv(inputfile,encoding = 'gbk') # 读取数据 data .info() # 查看数据属性 print("-"*40) print('描述性统计结果:\n',data.describe().T) # 输出结果
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 43367 entries, 0 to 43366
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 id 43367 non-null int64
1 Goods 43367 non-null object
dtypes: int64(1), object(1)
memory usage: 677.7+ KB
----------------------------------------
描述性统计结果:
count mean std min 25% 50% 75% max
id 43367.0 4908.589504 2843.118248 1.0 2455.5 4828.0 7380.5 9835.0
data.head()

2 分析热销商品
销量排行前10商品的销量及其占比
group = data.groupby(['Goods']).count().reset_index() # 对商品进行分类汇总 group_sorted=group.sort_values('id',ascending=False) print('销量排行前10商品的销量:\n', group_sorted[:10]) # 排序并查看前10位热销商品
销量排行前10商品的销量:
Goods id
7 全脂牛奶 2513
8 其他蔬菜 1903
155 面包卷 1809
134 苏打 1715
150 酸奶 1372
99 瓶装水 1087
70 根茎类蔬菜 1072
85 热带水果 1032
143 购物袋 969
160 香肠 924
x=group_sorted[:10]['Goods'] y=group_sorted[:10]['id'] plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号 plt.figure(figsize = (8, 4)) plt.barh(x,y) plt.xlabel('销量') plt.ylabel('商品类别') plt.title('商品的销量TOP10(3144)') plt.savefig('./top10.png')
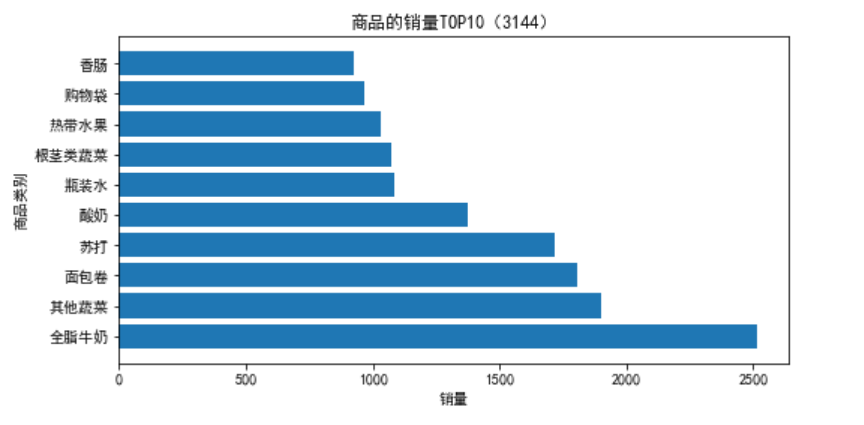
# 销量排行前10商品的销量占比 data_nums = data.shape[0] for idnex, row in group_sorted[:10].iterrows(): print(row['Goods'],row['id'],row['id']/data_nums)
全脂牛奶 2513 0.05794728710770863 其他蔬菜 1903 0.0438812922268084 面包卷 1809 0.04171374547466968 苏打 1715 0.039546198722530956 酸奶 1372 0.031636958978024765 瓶装水 1087 0.025065141697604168 根茎类蔬菜 1072 0.024719256577582033 热带水果 1032 0.023796896257523 购物袋 969 0.022344178753430026 香肠 924 0.021306523393363617
inputfile1 = '../data/GoodsOrder.csv' inputfile2 = '../data/GoodsTypes.csv' # 读入数据 data = pd.read_csv(inputfile1,encoding = 'gbk') types = pd.read_csv(inputfile2,encoding = 'gbk') group = data.groupby(['Goods']).count().reset_index() sort = group.sort_values('id',ascending = False).reset_index() data_nums = data.shape[0] # 总量 del sort['index'] # 合并两个datafreame,on='Goods' sort_links = pd.merge(sort,types) # 根据类别求和,每个商品类别的总量,并排序 sort_link = sort_links.groupby(['Types']).sum().reset_index() sort_link = sort_link.sort_values('id',ascending = False).reset_index() del sort_link['index'] # 删除“index”列 # 求百分比,然后更换列名,最后输出到文件 sort_link['count'] = sort_link.apply(lambda line: line['id']/data_nums,axis=1) sort_link.rename(columns = {'count':'percent'},inplace = True) print('各类别商品的销量及其占比:\n',sort_link) # 保存结果 outfile1 = '../tmp/percent.csv' sort_link.to_csv(outfile1,index = False,header = True,encoding='gbk')
各类别商品的销量及其占比:
Types id percent
0 非酒精饮料 7594 0.175110
1 西点 7192 0.165840
2 果蔬 7146 0.164780
3 米粮调料 5185 0.119561
4 百货 5141 0.118546
5 肉类 4870 0.112297
6 酒精饮料 2287 0.052736
7 食品类 1870 0.043120
8 零食 1459 0.033643
9 熟食 541 0.012475
data = sort_link['percent'] labels = sort_link['Types'] plt.figure(figsize=(8, 6)) plt.pie(data,labels=labels,autopct='%1.2f%%',shadow=False,startangle=90,normalize=False) plt.title('每类商品销量占比(3144)') plt.savefig('../tmp/persent.png') # 把图片以.png格式保存 plt.show()

通过分析各类别商品的销量及其占比情况可知,非酒精饮料、西点、果蔬3类商品的销量差距不大,占总销量的50%左右。
进一步查看销量第一的非酒精饮料类商品的内部商品结构,并绘制饼图显示其销量占比情况
# 先筛选“非酒精饮料”类型的商品,然后求百分比,然后输出结果到文件。 selected = sort_links.loc[sort_links['Types'] == '非酒精饮料'] # 对所有的“非酒精饮料”求和 child_nums = selected['id'].sum() # 求百分比 selected.loc[:,'child_percent'] = selected.apply(lambda line: line['id']/child_nums,axis = 1) selected.rename(columns = {'id':'count'},inplace = True) print('非酒精饮料内部商品的销量及其占比(3144):\n',selected) outfile2 = '../tmp/child_percent.csv' sort_link.to_csv(outfile2,index = False,header = True,encoding='gbk') # 输出结果
非酒精饮料内部商品的销量及其占比(3144):
Goods count Types child_percent
0 全脂牛奶 2513 非酒精饮料 0.330919
3 苏打 1715 非酒精饮料 0.225836
5 瓶装水 1087 非酒精饮料 0.143139
16 水果/蔬菜汁 711 非酒精饮料 0.093627
22 咖啡 571 非酒精饮料 0.075191
38 超高温杀菌的牛奶 329 非酒精饮料 0.043324
45 其他饮料 279 非酒精饮料 0.036740
51 一般饮料 256 非酒精饮料 0.033711
101 速溶咖啡 73 非酒精饮料 0.009613
125 茶 38 非酒精饮料 0.005004
144 可可饮料 22 非酒精饮料 0.002897
# 画饼图展示非酒精饮品内部各商品的销量占比 data = selected['child_percent'] labels = selected['Goods'] plt.figure(figsize = (8,6)) # 设置每一块分割出的间隙大小 explode = (0.02,0.03,0.04,0.05,0.06,0.07,0.08,0.08,0.3,0.1,0.3) plt.pie(data,explode = explode,labels = labels,autopct = '%1.2f%%', pctdistance = 1.1,labeldistance = 1.2,normalize=False) # 设置标题 plt.title("非酒精饮料内部各商品的销量占比(3144)") # 把单位长度都变的一样 plt.axis('equal') # 保存图形 plt.savefig('../tmp/child_persent.png') plt.show()
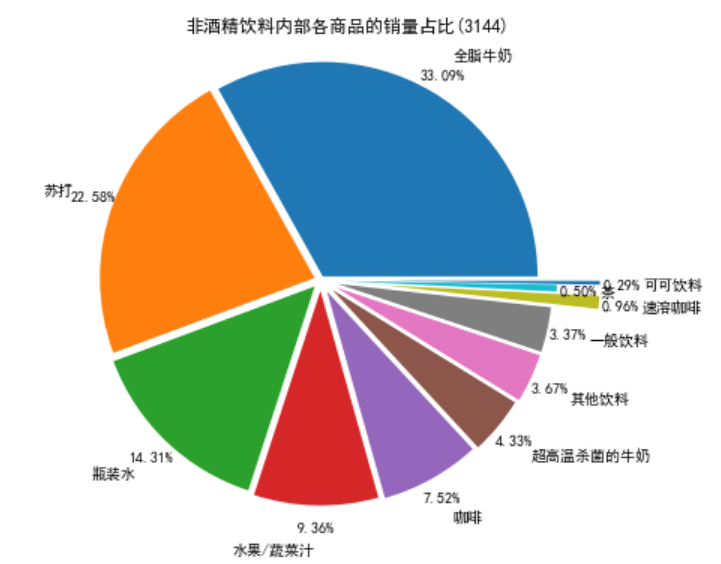
通过分析非酒精饮料内部商品的销量及其占比情况可知,全脂牛奶的销量在非酒精饮料的总销量中占比超过33%,前3种非酒精饮料的销量在非酒精饮料的总销量中的占比接近70%,这就说明大部分顾客到店购买的饮料为这3种,而商场就需要时常注意货物的库存,定期补货。
数据预处理
前面对数据探索分析发现数据完整,并不存在缺失值。建模之前需要转变数据的格式,才能使用Apriori函数进行关联分析。这里对数据进行转换。
import pandas as pd inputfile='../data/GoodsOrder.csv' data = pd.read_csv(inputfile,encoding = 'gbk') # 根据id对“Goods”列合并,并使用“,”将各商品隔开 data['Goods'] = data['Goods'].apply(lambda x:','+x) data = data.groupby('id').sum().reset_index() # 对合并的商品列转换数据格式 data['Goods'] = data['Goods'].apply(lambda x :[x[1:]]) data_list = list(data['Goods']) # 分割商品名为每个元素 data_translation = [] for i in data_list: p = i[0].split(',') data_translation.append(p) print('数据转换结果的前5个元素:\n', data_translation[0:5])
数据转换结果的前5个元素: [['柑橘类水果', '人造黄油', '即食汤', '半成品面包'], ['咖啡', '热带水果', '酸奶'], ['全脂牛奶'], ['奶油乳酪', '肉泥', '仁果类水果', '酸奶'], ['炼乳', '长面包', '其他蔬菜', '全脂牛奶']]
模型构建
本案例的目标是探索商品之间的关联关系,因此采用关联规则算法,以挖掘它们之间的关联关系。关联规则算法主要用于寻找数据中项集之间的关联关系,它揭示了数据项间的未知关系。基于样本的统计规律,进行关联规则分析。根据所分析的关联关系,可通过一个属性的信息来推断另一个属性的信息。当置信度达到某一阈值时,就可以认为规则成立。
Apriori算法是常用的关联规则算法之一,也是最为经典的分析频繁项集的算法,它是第一次实现在大数据集上可行的关联规则提取的算法。
模型具体实现步骤:
- 设置建模参数最小支持度、最小置信度,输入建模样本数据
- 采用Apriori关联规则算法对建模的样本数据进行分析,以模型参数设置的最小支持度、最小置信度以及分析目标作为条件,如果所有的规则都不满足条件,则需要重新调整模型参数,否则输出关联规则结果。
其关联规则代码如代码所示:
from numpy import * def loadDataSet(): return [['a', 'c', 'e'], ['b', 'd'], ['b', 'c'], ['a', 'b', 'c', 'd'], ['a', 'b'], ['b', 'c'], ['a', 'b'], ['a', 'b', 'c', 'e'], ['a', 'b', 'c'], ['a', 'c', 'e']] def createC1(dataSet): C1 = [] for transaction in dataSet: for item in transaction: if not [item] in C1: C1.append([item]) C1.sort() # 映射为frozenset唯一性的,可使用其构造字典 return list(map(frozenset, C1)) # 从候选K项集到频繁K项集(支持度计算) def scanD(D, Ck, minSupport): ssCnt = {} for tid in D: # 遍历数据集 for can in Ck: # 遍历候选项 if can.issubset(tid): # 判断候选项中是否含数据集的各项 if not can in ssCnt: ssCnt[can] = 1 # 不含设为1 else: ssCnt[can] += 1 # 有则计数加1 numItems = float(len(D)) # 数据集大小 retList = [] # L1初始化 supportData = {} # 记录候选项中各个数据的支持度 for key in ssCnt: support = ssCnt[key] / numItems # 计算支持度 if support >= minSupport: retList.insert(0, key) # 满足条件加入L1中 supportData[key] = support return retList, supportData def calSupport(D, Ck, min_support): dict_sup = {} for i in D: for j in Ck: if j.issubset(i): if not j in dict_sup: dict_sup[j] = 1 else: dict_sup[j] += 1 sumCount = float(len(D)) supportData = {} relist = [] for i in dict_sup: temp_sup = dict_sup[i] / sumCount if temp_sup >= min_support: relist.append(i) # 此处可设置返回全部的支持度数据(或者频繁项集的支持度数据) supportData[i] = temp_sup return relist, supportData # 改进剪枝算法 def aprioriGen(Lk, k): retList = [] lenLk = len(Lk) for i in range(lenLk): for j in range(i + 1, lenLk): # 两两组合遍历 L1 = list(Lk[i])[:k - 2] L2 = list(Lk[j])[:k - 2] L1.sort() L2.sort() if L1 == L2: # 前k-1项相等,则可相乘,这样可防止重复项出现 # 进行剪枝(a1为k项集中的一个元素,b为它的所有k-1项子集) a = Lk[i] | Lk[j] # a为frozenset()集合 a1 = list(a) b = [] # 遍历取出每一个元素,转换为set,依次从a1中剔除该元素,并加入到b中 for q in range(len(a1)): t = [a1[q]] tt = frozenset(set(a1) - set(t)) b.append(tt) t = 0 for w in b: # 当b(即所有k-1项子集)都是Lk(频繁的)的子集,则保留,否则删除。 if w in Lk: t += 1 if t == len(b): retList.append(b[0] | b[1]) return retList def apriori(dataSet, minSupport=0.2): # 前3条语句是对计算查找单个元素中的频繁项集 C1 = createC1(dataSet) D = list(map(set, dataSet)) # 使用list()转换为列表 L1, supportData = calSupport(D, C1, minSupport) L = [L1] # 加列表框,使得1项集为一个单独元素 k = 2 while (len(L[k - 2]) > 0): # 是否还有候选集 Ck = aprioriGen(L[k - 2], k) Lk, supK = scanD(D, Ck, minSupport) # scan DB to get Lk supportData.update(supK) # 把supk的键值对添加到supportData里 L.append(Lk) # L最后一个值为空集 k += 1 del L[-1] # 删除最后一个空集 return L, supportData # L为频繁项集,为一个列表,1,2,3项集分别为一个元素 # 生成集合的所有子集 def getSubset(fromList, toList): for i in range(len(fromList)): t = [fromList[i]] tt = frozenset(set(fromList) - set(t)) if not tt in toList: toList.append(tt) tt = list(tt) if len(tt) > 1: getSubset(tt, toList) def calcConf(freqSet, H, supportData, ruleList, minConf=0.7): for conseq in H: #遍历H中的所有项集并计算它们的可信度值 conf = supportData[freqSet] / supportData[freqSet - conseq] # 可信度计算,结合支持度数据 # 提升度lift计算lift = p(a & b) / p(a)*p(b) lift = supportData[freqSet] / (supportData[conseq] * supportData[freqSet - conseq]) if conf >= minConf and lift > 1: print(freqSet - conseq, '-->', conseq, '支持度', round(supportData[freqSet], 6), '置信度:', round(conf, 6), 'lift值为:', round(lift, 6)) ruleList.append((freqSet - conseq, conseq, conf)) # 生成规则 def gen_rule(L, supportData, minConf = 0.7): bigRuleList = [] for i in range(1, len(L)): # 从二项集开始计算 for freqSet in L[i]: # freqSet为所有的k项集 # 求该三项集的所有非空子集,1项集,2项集,直到k-1项集,用H1表示,为list类型,里面为frozenset类型, H1 = list(freqSet) all_subset = [] getSubset(H1, all_subset) # 生成所有的子集 calcConf(freqSet, all_subset, supportData, bigRuleList, minConf) return bigRuleList if __name__ == '__main__': dataSet = data_translation L, supportData = apriori(dataSet, minSupport = 0.02) rule = gen_rule(L, supportData, minConf = 0.35)
frozenset({'水果/蔬菜汁'}) --> frozenset({'全脂牛奶'}) 支持度 0.02664 置信度: 0.368495 lift值为: 1.44216
frozenset({'人造黄油'}) --> frozenset({'全脂牛奶'}) 支持度 0.024199 置信度: 0.413194 lift值为: 1.617098
frozenset({'仁果类水果'}) --> frozenset({'全脂牛奶'}) 支持度 0.030097 置信度: 0.397849 lift值为: 1.557043
frozenset({'牛肉'}) --> frozenset({'全脂牛奶'}) 支持度 0.021251 置信度: 0.405039 lift值为: 1.58518
frozenset({'冷冻蔬菜'}) --> frozenset({'全脂牛奶'}) 支持度 0.020437 置信度: 0.424947 lift值为: 1.663094
frozenset({'本地蛋类'}) --> frozenset({'其他蔬菜'}) 支持度 0.022267 置信度: 0.350962 lift值为: 1.813824
frozenset({'黄油'}) --> frozenset({'其他蔬菜'}) 支持度 0.020031 置信度: 0.361468 lift值为: 1.868122
frozenset({'本地蛋类'}) --> frozenset({'全脂牛奶'}) 支持度 0.029995 置信度: 0.472756 lift值为: 1.850203
frozenset({'黑面包'}) --> frozenset({'全脂牛奶'}) 支持度 0.025216 置信度: 0.388715 lift值为: 1.521293
frozenset({'糕点'}) --> frozenset({'全脂牛奶'}) 支持度 0.033249 置信度: 0.373714 lift值为: 1.462587
frozenset({'酸奶油'}) --> frozenset({'其他蔬菜'}) 支持度 0.028876 置信度: 0.402837 lift值为: 2.081924
frozenset({'猪肉'}) --> frozenset({'其他蔬菜'}) 支持度 0.021657 置信度: 0.375661 lift值为: 1.941476
frozenset({'酸奶油'}) --> frozenset({'全脂牛奶'}) 支持度 0.032232 置信度: 0.449645 lift值为: 1.759754
frozenset({'猪肉'}) --> frozenset({'全脂牛奶'}) 支持度 0.022166 置信度: 0.38448 lift值为: 1.504719
frozenset({'根茎类蔬菜'}) --> frozenset({'全脂牛奶'}) 支持度 0.048907 置信度: 0.448694 lift值为: 1.756031
frozenset({'根茎类蔬菜'}) --> frozenset({'其他蔬菜'}) 支持度 0.047382 置信度: 0.434701 lift值为: 2.246605
frozenset({'凝乳'}) --> frozenset({'全脂牛奶'}) 支持度 0.026131 置信度: 0.490458 lift值为: 1.919481
frozenset({'热带水果'}) --> frozenset({'全脂牛奶'}) 支持度 0.042298 置信度: 0.403101 lift值为: 1.577595
frozenset({'柑橘类水果'}) --> frozenset({'全脂牛奶'}) 支持度 0.030503 置信度: 0.36855 lift值为: 1.442377
frozenset({'黄油'}) --> frozenset({'全脂牛奶'}) 支持度 0.027555 置信度: 0.497248 lift值为: 1.946053
frozenset({'酸奶'}) --> frozenset({'全脂牛奶'}) 支持度 0.056024 置信度: 0.401603 lift值为: 1.571735
frozenset({'其他蔬菜'}) --> frozenset({'全脂牛奶'}) 支持度 0.074835 置信度: 0.386758 lift值为: 1.513634
frozenset({'全脂牛奶', '酸奶'}) --> frozenset({'其他蔬菜'}) 支持度 0.022267 置信度: 0.397459 lift值为: 2.054131
frozenset({'其他蔬菜', '酸奶'}) --> frozenset({'全脂牛奶'}) 支持度 0.022267 置信度: 0.512881 lift值为: 2.007235
frozenset({'全脂牛奶', '根茎类蔬菜'}) --> frozenset({'其他蔬菜'}) 支持度 0.023183 置信度: 0.474012 lift值为: 2.44977
frozenset({'根茎类蔬菜', '其他蔬菜'}) --> frozenset({'全脂牛奶'}) 支持度 0.023183 置信度: 0.48927 lift值为: 1.914833
根据输出结果,对其中4条进行解释分析如下:
- {'其他蔬菜','酸奶'}=>{'全脂牛奶'}支持度约为2.23%,置信度约为51.29%。说明同时购买酸奶、其他蔬菜和全脂牛奶这3种商品的概率达51.29%,而这种情况发生的可能性约为2.23%。
- {'其他蔬菜'}=>{'全脂牛奶'}支持度最大约为7.48%,置信度约为38.68%。说明同时购买其他蔬菜和全脂牛奶这两种商品的概率达38.68%,而这种情况发生的可能性约为7.48%。
- {'根茎类蔬菜'}=>{'全脂牛奶'}支持度约为4.89%,置信度约为44.87%。说明同时购买根茎类蔬菜和全脂牛奶这3种商品的概率达44.87%,而这种情况发生的可能性约为4.89%。
- {'根茎类蔬菜'}=>{'其他蔬菜'}支持度约为4.74%,置信度约为43.47%。说明同时购买根茎类蔬菜和其他蔬菜这两种商品的概率达43.47%,而这种情况发生的可能性约为4.74%。
由上分析可知,顾客购买酸奶和其他蔬菜的时候会同时购买全脂牛奶,其置信度最大达到51.29%。因此,顾客同时购买其他蔬菜、根茎类蔬菜和全脂牛奶的概率较高。
对于模型结果,从购物者角度进行分析:现代生活中,大多数购物者为“家庭煮妇”,购买的商品大部分是食品,随着生活质量的提高和健康意识的增加,其他蔬菜、根茎类蔬菜和全脂牛奶均为现代家庭每日饮食的所需品。因此,其他蔬菜、根茎类蔬菜和全脂牛奶同时购买的概率较高,符合人们的现代生活健康意识。
模型应用
模型结果表明:顾客购买其他商品的时候会同时购买全脂牛奶。因此,商场应该根据实际情况将全脂牛奶放在顾客购买商品的必经之路上,或是放在商场显眼的位置,以方便顾客拿取。顾客同时购买其他蔬菜、根茎类蔬菜、酸奶油、猪肉、黄油、本地蛋类和多种水果的概率较高,因此商场可以考虑捆绑销售,或者适当调整商场布置,将这些商品的距离尽量拉近,从而提升顾客的购物体验。
第二部分 对西点分析
# 先筛选“非酒精饮料”类型的商品,然后求百分比,然后输出结果到文件。 selected = sort_links.loc[sort_links['Types'] == '西点'] # 对所有的“非酒精饮料”求和 westernsnake_nums = selected['id'].sum() # 求百分比 selected.loc[:,'westernsnake_percent'] = selected.apply(lambda line: line['id']/westernsnake_nums,axis = 1) selected.rename(columns = {'id':'count'},inplace = True) print('非酒精饮料内部商品的销量及其占比(3144):\n',selected) outfile2 = 'D:/Desktop/westernsnake_percent.csv' sort_link.to_csv(outfile2,index = False,header = True,encoding='gbk') # 输出结果
非酒精饮料内部商品的销量及其占比(3144):
Goods count Types westernsnake_percent
2 面包卷 1809 西点 0.251529
10 糕点 875 西点 0.121663
18 黑面包 638 西点 0.088710
31 白面包 414 西点 0.057564
32 奶油乳酪 390 西点 0.054227
33 威化饼 378 西点 0.052558
34 咸点心 372 西点 0.051724
35 长面包 368 西点 0.051168
36 甜点 365 西点 0.050751
48 酪 275 西点 0.038237
54 切片奶酪 241 西点 0.033509
55 硬奶酪 241 西点 0.033509
64 半成品面包 174 西点 0.024194
68 软奶酪 168 西点 0.023359
74 风味蛋糕 130 西点 0.018076
92 甜食 89 西点 0.012375
94 特色奶酪 84 西点 0.011680
103 面包干 68 西点 0.009455
116 干面包 50 西点 0.006952
117 凝乳酪 50 西点 0.006952
152 奶油 13 西点 0.001808
# 画饼图展示西点内部各商品的销量占比 data = selected['westernsnake_percent'] labels = selected['Goods'] plt.figure(figsize = (8,6)) # 设置每一块分割出的间隙大小 explode = (0.02,0.03,0.04,0.05,0.06,0.07,0.08,0.08,0.3,0.1,0.3,0.02,0.03,0.04,0.05,0.06,0.07,0.08,0.08,0.3,0.1) plt.pie(data,explode = explode,labels = labels,autopct = '%1.2f%%', pctdistance = 1.1,labeldistance = 1.2) # 设置标题 plt.title("西点内部各商品的销量占比 ") # 把单位长度都变的一样 plt.axis('equal') # 保存图形 plt.savefig('D:/Desktop/westernsnake_persent.png')
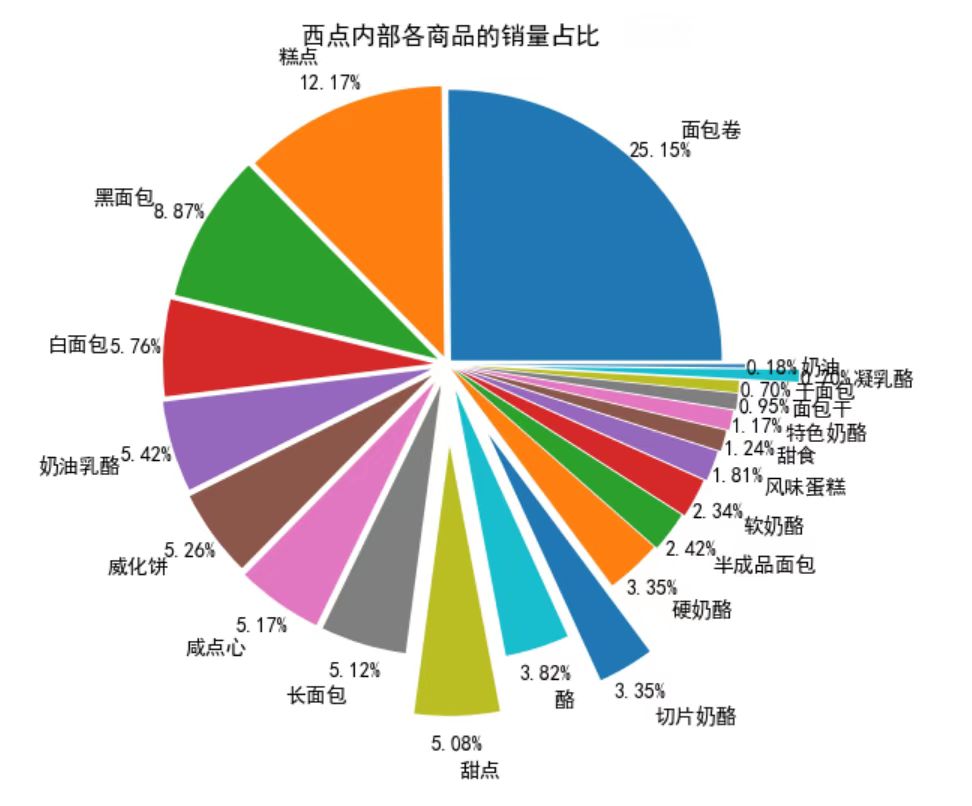






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本