[ACM_其他] Square Ice (poj1099 规律)
Description
Square Ice is a two-dimensional arrangement of water molecules H2O, with oxygen at the vertices of a square lattice and one hydrogen atom between each pair of adjacent oxygen atoms. The hydrogen atoms must stick out on the left and right sides but are not allowed to stick out the top or bottom. One 5 x 5 example is shown below.
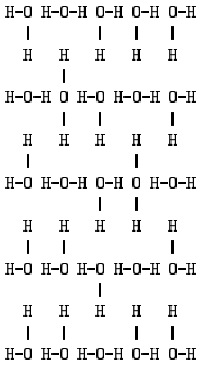
Note that each hydrogen atom is attached to exactly one of its neighboring oxygen atoms and each oxygen atom is attached to two of its neighboring hydrogen atoms. (Recall that one water molecule is a unit of one O linked to two H's.)
It turns out we can encode a square ice pattern with what is known as an alternating sign matrix (ASM): horizontal molecules are encoded as 1, vertical molecules are encoded as -1 and all other molecules are encoded as 0. So, the above pattern would be encoded as:
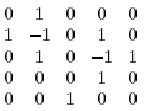
An ASM is a square matrix with entries 0, 1 and -1, where the sum of each row and column is 1 and the non-zero entries in each row and in each column must alternate in sign. (It turns out there is a one-to-one correspondence between ASM's and square ice patterns!)
Your job is to display the square ice pattern, in the same format as the example above, for a given ASM. Use dashes (-) for horizontal attachments and vertical bars (|) for vertical attachments. The pattern should be surrounded with a border of asterisks (*), be left justified and there should be exactly one character between neighboring hydrogen atoms (H) and oxygen atoms (O): either a space, a dash or a vertical bar.
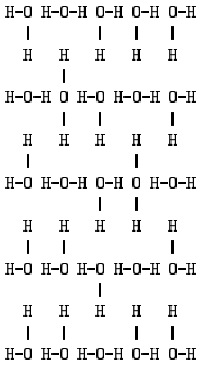
Note that each hydrogen atom is attached to exactly one of its neighboring oxygen atoms and each oxygen atom is attached to two of its neighboring hydrogen atoms. (Recall that one water molecule is a unit of one O linked to two H's.)
It turns out we can encode a square ice pattern with what is known as an alternating sign matrix (ASM): horizontal molecules are encoded as 1, vertical molecules are encoded as -1 and all other molecules are encoded as 0. So, the above pattern would be encoded as:
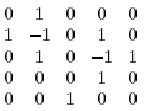
An ASM is a square matrix with entries 0, 1 and -1, where the sum of each row and column is 1 and the non-zero entries in each row and in each column must alternate in sign. (It turns out there is a one-to-one correspondence between ASM's and square ice patterns!)
Your job is to display the square ice pattern, in the same format as the example above, for a given ASM. Use dashes (-) for horizontal attachments and vertical bars (|) for vertical attachments. The pattern should be surrounded with a border of asterisks (*), be left justified and there should be exactly one character between neighboring hydrogen atoms (H) and oxygen atoms (O): either a space, a dash or a vertical bar.
Input
Input consists of multiple cases. Each case consists of a positive integer m (<= 11) on a line followed by m lines giving the entries of an ASM. Each line gives a row of the ASM with entries separated by a single space. The end of input is indicated by a line containing m = 0.
Output
For each case, print the case number (starting from 1), in the format shown in the Sample Output, followed by a blank line, followed by the corresponding square ice pattern in the format described above. Separate the output of different cases by a blank line.
Sample Input
2 0 1 1 0 4 0 1 0 0 1 -1 0 1 0 0 1 0 0 1 0 0 0
Sample Output
Case 1: *********** *H-O H-O-H* * | * * H H * * | * *H-O-H O-H* *********** Case 2: ******************* *H-O H-O-H O-H O-H* * | | | * * H H H H * * | * *H-O-H O H-O H-O-H* * | | * * H H H H * * | | * *H-O H-O H-O-H O-H* * | * * H H H H * * | | | * *H-O H-O-H O-H O-H* *******************
Source
题目的大致意思就是给你一个矩阵,里面包含有1,-1,或者0,分别代表三种水分子的排列方式,现在要求根据矩阵来还原水分子的排列,并在周围加上一圈的“*”。仔细观察会发现其实H和O的分布是不变的,唯一不同的是氢氧建的位置,我首先把H和O的位置放好,然后分别根据横竖排列限制确定某些H(这里游离H用4表示,非游离的用5来表示),然后针对非竖非横的排列情况单独分析该氧元素周围4个氢原子的情况。(特别说明:这里用square[i][j]来标记(i,j)位置的对应符号,最后才把结果输出来)
1 #include<iostream> 2 #include<string.h> 3 using namespace std; 4 int n,ASM[12][12],square[50][50];//square[][]用来存放结果符号映射,其中set[square[i][j]]即为i,j位置的符号 5 char set[]={' ','-','|','O','H','H'};//4代表游离H,5代表固定H 6 bool Valid(int i,int j){return (0<=i&&i<4*n-3&&0<=j&&j<4*n+1);} 7 void output(){ 8 for(int i=0;i<4*n+3;i++) cout<<'*';cout<<'\n';//输出第一行的4n+3个* 9 for(int i=0;i<4*n-3;i++){//中间图像 10 cout<<'*'; 11 for(int j=0;j<4*n+1;j++)cout<<set[square[i][j]]; 12 cout<<'*'<<'\n'; 13 } 14 for(int i=0;i<4*n+3;i++) cout<<'*';cout<<'\n';//输出最后一行的4n+3个* 15 } 16 void solve(){ 17 memset(square,0,sizeof(square)); 18 for(int i=0;i<n;i++){ 19 for(int j=0;j<n;j++){ 20 square[4*i][4*j+2]=3;square[4*i][4*j+4]=4; 21 if(j==0) square[4*i][4*j]=4; 22 if(i<n-1) square[4*i+2][4*j+2]=4; //氧氢位置是固定的,变化的是连线!!! 23 24 if(ASM[i][j]==1){//横着 25 square[4*i][4*j+1]=square[4*i][4*j+3]=1; 26 square[4*i][4*j]=square[4*i][4*j+4]=5; 27 } 28 else if(ASM[i][j]==-1){//竖着(不用考虑越界因为i不可能为0) 29 square[4*i-1][4*j+2]=square[4*i+1][4*j+2]=2; 30 square[4*i-2][4*j+2]=square[4*i+2][4*j+2]=5; 31 } 32 } 33 } 34 for(int i=0;i<n;i++){//其他情况配对 35 for(int j=0;j<n;j++){ 36 if(ASM[i][j]==0){//对i,j周围4个H进行判断,并固定其中游离的H 37 if(Valid(4*i,4*j)&&square[4*i][4*j]!=5) 38 square[4*i][4*j]=5, square[4*i][4*j+1]=1; 39 else if(Valid(4*i,4*j+4)&&square[4*i][4*j+4]!=5) 40 square[4*i][4*j+4]=5, square[4*i][4*j+3]=1; 41 if(Valid(4*i-2,4*j+2)&&square[4*i-2][4*j+2]!=5) 42 square[4*i-2][4*j+2]=5, square[4*i-1][4*j+2]=2; 43 else if(Valid(4*i+2,4*j+2)&&square[4*i+2][4*j+2]!=5) 44 square[4*i+2][4*j+2]=5, square[4*i+1][4*j+2]=2; 45 } 46 } 47 } 48 } 49 int main(){ 50 int casee=1; 51 while(cin>>n && n>0){ 52 for(int i=0;i<n;i++) 53 for(int j=0;j<n;j++) 54 cin>>ASM[i][j]; 55 cout<<(casee==1 ? "":"\n"); 56 cout<<"Case "<<casee++<<":\n\n"; 57 solve(); 58 output(); 59 }return 0; 60 } 61 //poj1099


