[ACM_几何] Fishnet

 

http://acm.hust.edu.cn/vjudge/contest/view.action?cid=28417#problem/C

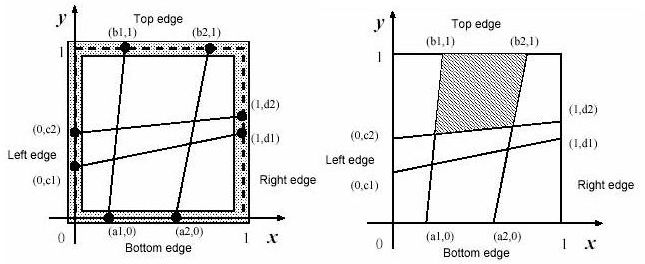
本题大意：有一个1X1的矩形，每边按照从小到大的顺序给n个点如图，然后对应连线将举行划分，求最大面积。

解题思路：暴力算出各点，求出各面积

 

#include<iostream>
#include<cmath>
#include<string.h>
#include<string>
#include<stdio.h>
#include<algorithm>
#include<iomanip>

using namespace std;
#define eps 0.0000000001
#define PI acos(-1.0)


//点和向量
struct Point{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y){}
};
typedef Point Vector;
Vector operator+(Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
Vector operator-(Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
Vector operator*(Vector a,double p){return Vector(a.x*p,a.y*p);}
Vector operator/(Vector a,double p){return Vector(a.x/p,a.y/p);}
bool operator<(const Vector& a,const Vector& b){return a.x<b.x||(a.x==b.x && a.y<b.y);}
int dcmp(double x){
    if(fabs(x)<eps)return 0;
    else return x<0 ? -1:1;
}
bool operator==(const Point& a,const Point& b){
    return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;
}
double Dot(Vector A,Vector B){return A.x*B.x+A.y*B.y;}//向量点积
double Length(Vector A){return sqrt(Dot(A,A));}//向量模长
double Angle(Vector A,Vector B){return acos(Dot(A,B)/Length(A)/Length(B));}//向量夹角
double Cross(Vector A,Vector B){return A.x*B.y-A.y*B.x;}
double Area2(Point A,Point B,Point C){return Cross(B-A,C-A);}//三角形面积的2倍
//绕起点逆时针旋转rad度
Vector Rotate(Vector A,double rad){          
    return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
double torad(double jiao){return jiao/180*PI;}//角度转弧度
double tojiao(double ang){return ang/PI*180;}//弧度转角度 
//单位法向量
Vector Normal(Vector A){
    double L=Length(A);
    return Vector(-A.y/L,A.x/L);
}
//点和直线
struct Line{
    Point P;//直线上任意一点
    Vector v;//方向向量，他的左边对应的就是半平面
    double ang;//极角，即从x正半轴旋转到向量v所需的角（弧度）
    Line(){}
    Line(Point p,Vector v):P(p),v(v){ang=atan2(v.y,v.x);}
    bool operator<(const Line& L)const {
        return ang<L.ang;
    }
};
//计算直线P+tv和Q+tw的交点（计算前必须确保有唯一交点）即：Cross(v,w)非0
Point GetLineIntersection(Point P,Vector v,Point Q,Vector w){
    Vector u=P-Q;
    double t=Cross(w,u)/Cross(v,w);
    return P+v*t;
}
//点到直线距离(dis between point P and line AB)
double DistanceToLine(Point P,Point A,Point B){
    Vector v1=B-A , v2=P-A;
    return fabs(Cross(v1,v2))/Length(v1);
}
//dis between point P and segment AB
double DistancetoSegment(Point P,Point A,Point B){
    if(A==B)return Length(P-A);
    Vector v1=B-A,v2=P-A,v3=P-B;
    if(dcmp(Dot(v1,v2))<0)return  Length(v2);
    else if(dcmp(Dot(v1,v3))>0)return Length(v3);
    else return fabs(Cross(v1,v2))/Length(v1);
}
//point P on line AB 投影点
Point GetLineProjection(Point P,Point A,Point B){
    Vector v=B-A;
    return A+v*(Dot(v,P-A)/Dot(v,v));
}
//线段规范相交（只有一个且不在端点）每条线段两端都在另一条两侧，（叉积符号不同）
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2){
    double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1),
           c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-b1);
    return dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0;
}
//判断点P是否在线段AB上
bool OnSegment(Point p,Point a1,Point a2){
    return dcmp(Cross(a1-p,a2-p))==0 && dcmp(Dot(a1-p,a2-p))<0;
}
//多边形的面积（可以是非凸多边形）
double PolygonArea(Point* p,int n){
    double area=0;
    for(int i=1;i<n-1;i++)
        area+=Cross(p[i]-p[0],p[i+1]-p[0]);
    return area/2;
}


//点p在有向直线左边，上面不算
bool OnLeft(Line L,Point p){
    return Cross(L.v,p-L.P)>0;
}

double ok(double x,double y,double d,double z){
    double f=fabs(d*(1/tan(acos(z/y))+1/tan(acos(z/x))))-z;
    if(fabs(f)<1e-4)return  0;
    else return f;
}
//计算凸包输入点数组p，个数n，输出点数组ch，返回凸包定点数
//输入不能有重复，完成后输入点顺序被破坏
//如果不希望凸包的边上有输入点，把两个<=改成<
//精度要求高时，建议用dcmp比较
//基于水平的Andrew算法-->1、点排序2、删除重复的然后把前两个放进凸包
//3、从第三个往后当新点在凸包前进左边时继续，否则一次删除最近加入的点，直到新点在左边
int ConVexHull(Point* p,int n,Point*ch){
    sort(p,p+n);
    int m=0;
    for(int i=0;i<n;i++){//下凸包
        while(m>1 && Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)m--;
        ch[m++]=p[i];
    }
    int k=m;
    for(int i=n-2;i>=0;i--){//上凸包
        while(m>k && Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)m--;
        ch[m++]=p[i];
    }
    if(n>1)m--;
    return m;
}
int main(){
    Point point[33][33];
    Point a[33],b[33],c[33],d[33];
    for(int n;cin>>n&&n;){

        point[0][0].x=0;
        point[0][0].y=0;
        for(int i=0;i<n;i++){
            cin>>a[i].x;
            a[i].y=0;
            point[0][i+1]=a[i];
        }

        point[n+1][n+1].x=1;
        point[n+1][n+1].y=1;
        for(int i=0;i<n;i++){
            cin>>b[i].x;
            b[i].y=1;
            point[n+1][i+1]=b[i];
        }

        point[n+1][0].x=0;
        point[n+1][0].y=1;
        for(int i=0;i<n;i++){
            cin>>c[i].y;
            c[i].x=0;
            point[i+1][0]=c[i];
        }

        point[0][n+1].x=1;
        point[0][n+1].y=0;
        for(int i=0;i<n;i++){
            cin>>d[i].y;
            d[i].x=1;
            point[i+1][n+1]=d[i];
        }

        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                point[i+1][j+1]=GetLineIntersection(c[i],d[i]-c[i],a[j],b[j]-a[j]);
            }
        }

        Point four[4];
        double max=-1,area;
        for(int i=0;i<=n;i++){
            for(int j=0;j<=n+1;j++){
                four[0]=point[i][j];
                four[1]=point[i][j+1];
                four[2]=point[i+1][j+1];
                four[3]=point[i+1][j];
                area=PolygonArea(four,4);
                if(area>max)max=area;
            }
        }
        cout<<fixed<<max<<'\n';
    }return 0;
}