torch.Tensor.backward()简单使用
前言
在深度学习中,经常需要对函数求梯度(gradient)。PyTorch提供的autograd包能够根据输入和前向传播过程自动构建计算图,并执行反向传播。本文主要通过例子来介绍一下pytorch中torch.Tensor.backward()的简单用法。
标量变量的反向传播
PyTorch中,torch.Tensor是存储和变换数据的主要工具。如果你之前用过NumPy,你会发现Tensor和NumPy的多维数组非常类似。然而,Tensor提供GPU计算和自动求梯度等更多功能,这些使Tensor更加适合深度学习。
如果将PyTorch中的tensor属性requires_grad设置为True,它将开始追踪(track)在其上的所有操作(这样就可以利用链式法则进行梯度传播了)。完成计算后,可以调用backward()来完成所有梯度计算。此tensor的梯度将累积到grad属性中。
下面我们来看一个例子。
import torch
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = x ** 2 + 2
z = torch.sum(y)
z.backward()
print(x.grad)
tensor([2., 4., 6.])
下面先解释下这个grad怎么算的。
设\(x=[x_1,x_2,x_3]\),则

由求偏导的数学知识,可知:
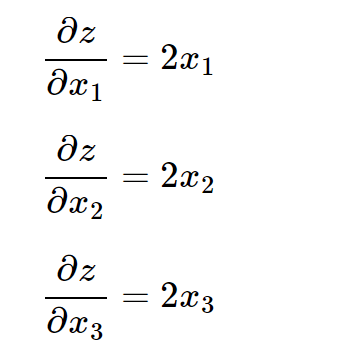
然后把\(x_1=1.0,x_2=2.0,x_3=3.0\)代入得到:
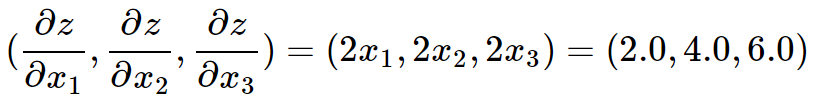
可见结果与PyTorch的输出一致。
非标量变量的反向传播
同样,先看下面的例子。已知,
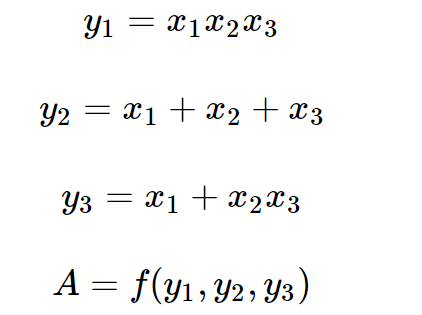
其中函数\(f(y_1,y_2,y_3)\)的具体定义未知,现在求:
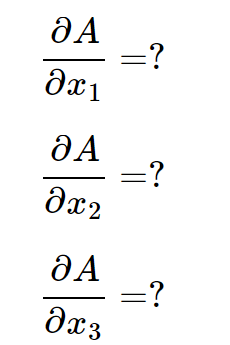
根据多元复合函数的求导法则,有:
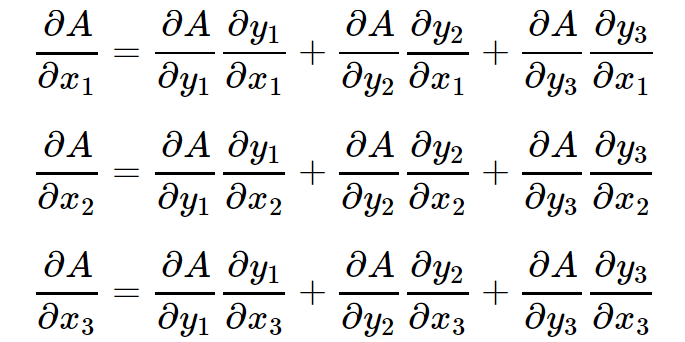
上面3个等式可以写成矩阵相乘的形式,如下:
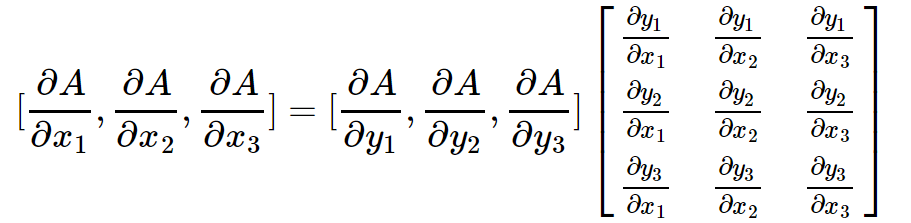
其中
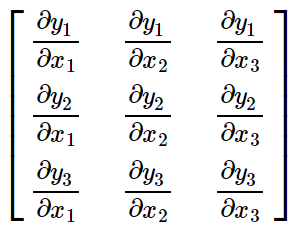
叫作雅可比(Jacobian)式。雅可比式可以根据已知条件求出。
现在只要知道\([\frac{\partial A}{\partial y_1},\frac{\partial A}{\partial y_2},\frac{\partial A}{\partial y_3}]\)的值,哪怕不知道\(f(y_1,y_2,y_3)\)的具体形式也能求出来\([\frac{\partial A}{\partial x_1},\frac{\partial A}{\partial x_2},\frac{\partial A}{\partial x_3}]\).
那现在的问题是怎么样才能求出
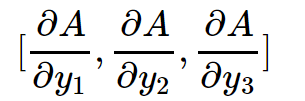
答案是由PyTorch的backward函数的gradient参数提供。这就是gradient参数的作用。
比如,我们传入gradient参数为torch.tensor([0.1, 0.2, 0.3], dtype=torch.float),并且假定\(x_1=1,x_2=2,x_3=3\),按照上面的推导方法:
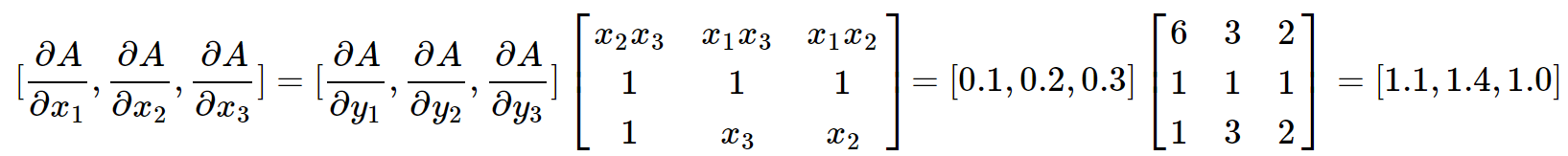
我们可以用代码验证一下:
import torch
x1 = torch.tensor(1, requires_grad=True, dtype=torch.float)
x2 = torch.tensor(2, requires_grad=True, dtype=torch.float)
x3 = torch.tensor(3, requires_grad=True, dtype=torch.float)
x = torch.tensor([x1, x2, x3])
y = torch.randn(3)
y[0] = x1 * x2 * x3
y[1] = x1 + x2 + x3
y[2] = x1 + x2 * x3
y.backward(torch.tensor([0.1, 0.2, 0.3], dtype=torch.float))
print(x1.grad, x2.grad, x3.grad)
tensor(1.1000) tensor(1.4000) tensor(1.)
由此可见,推导和代码运行结果一致。
当\(y\)不是标量时,向量\(y\)关于向量\(x\)的导数的最自然解释是⼀个矩阵。对于高阶和高维的\(y\)和\(x\),求导的结果可以是⼀个高阶张量。
然而,虽然这些更奇特的对象确实出现在高级机器学习中(包括深度学习中),但当我们调用向量的反向计算时,我们通常会试图计算一批训练样本中每个组成部分的(这里我的理解是关于非标量\(y\)的各个维度的)损失函数的导数。这里,我们的目的不是计算微分矩阵,而是单独计算批量中每个样本的(这里我的理解是关于非标量\(y\)的各个维度的)偏导数之和。对非标量,调⽤backward,需要传⼊⼀个gradient参数,该参数指定微分函数关于self的梯度。
import torch
x = torch.arange(4.0)
y = x * x
# 等价于y.sum().backward()
y.backward(torch.ones(len(x)))
x.grad
tensor([0., 2., 4., 6.])
参考
https://medium.com/@monadsblog/pytorch-backward-function-e5e2b7e60140
https://zhuanlan.zhihu.com/p/447129403
https://zhuanlan.zhihu.com/p/83172023


