隐马尔科夫模型HMM、最大熵马尔科夫模型MEMM、条件随机场CRF

目录

• HMM
  • HMM简介
  • HMM应用于中文分词
  • Jieba分词HMM例子
• 2-HMM
  • 预备知识
    • n-gram语法模型
    • 两种CWS模型
    • HMM分词
  • TnT
  • Character-Based Generative Model
  • 例子
• MEMM
  • 预备知识
    • 概率图模型
    • HMM
    • 最大熵模型
  • 最大熵马尔科夫模型
  • MEMM缺陷
• CRF

Nianwen Xue在《Chinese Word Segmentation as Character Tagging》中将中文分词视作为序列标注问题（sequence tagging problem），由此引入监督学习算法来解决分词问题。

HMM

HMM简介

首先，我们将简要地介绍HMM（主要参考了李航老师的《统计学习方法》）。HMM包含如下的五元组：

• 状态值集合\(Q=\{q_1,q_2,⋯,q_N\}\)，其中\(N\)为可能的状态数；
• 观测值集合\(V=\{v_1,v_2,⋯,v_M\}\)，其中\(M\)为可能的观测数；
• 转移概率矩阵\(A=[a_{ij}]\)，其中\(a_{ij}\)表示从状态\(i\)转移到状态\(j\)的概率；
• 发射概率矩阵（也称之为观测概率矩阵）\(B=[b_j(k)]\)，其中\(b_j(k)\)表示在状态j的条件下生成观测\(v_k\)的概率；
• 初始状态分布\(π\).

一般地，将HMM表示为模型\(λ=(A,B,π)\)，状态序列为\(I\)，对应测观测序列为\(O\)。对于这三个基本参数，HMM有三个基本问题：

• 概率计算问题，在模型\(λ\)下,观测序列\(O\)出现的概率；
• 学习问题，已知观测序列\(O\)，估计模型\(λ\)的参数，使得在该模型下,观测序列\(P(O|λ)\)最大；
• 解码（decoding）问题，已知模型λ与观测序列O，求解条件概率\(P(I|O)\)最大的状态序列\(I\)。

HMM应用于中文分词

将状态值集合\(Q\)置为\(\{B,E,M,S\}\)，分别表示词的开始、结束、中间(begin、end、middle)及字符独立成词(single)；观测序列即为中文句子。比如，“今天天气不错”,通过HMM求解得到状态序列“B E B E B E”，则分词结果为“今天/天气/不错”。

通过上面例子，我们发现中文分词的任务对应于解码问题：对于字符串\(C=\{c_1,⋯,c_n\}\)，求解最大条件概率

$\max \space P(t_1,⋯,t_n|c_1,⋯,c_n)$

其中，\(t_i\)表示字符\(c_i\)对应的状态。应如何求解状态序列呢？解决的办法便是Viterbi算法；其实，Viterbi算法本质上是一个动态规划算法，利用到了状态序列的最优路径满足这样一个特性：最优路径的子路径也一定是最优的。定义在时刻\(t\)状态为\(i\)的概率最大值为\(δ_t(i)\)，则有递推公式：

$δ_{t+1}(i) = \max \limits_j [δ_t(j)a_{ji}]b_i(o_{t+1})$

其中，\(o_{t+1}\)即为字符\(c_{t+1}\)。

Jieba分词HMM例子

Jieba的jieba.finalseg实现HMM中文分词。

from jieba.finalseg import cut
sentence = "小明硕士毕业于中国科学院计算所，后在日本京都大学深造"
print('/'.join(cut(sentence)))

分词结果为:
"小明/硕士/毕业于/中国/科学院/计算/所/，/后/在/日/本京/都/大学/深造"

我们发现：关于“日本京都”出现分词错误的情况。这是因为

• 最大条件概率\(P(I|O)\)对应的状态序列不一定是分词正确的标注序列(个人：也就是使用的这种建模方式，并不一定和实际的情况相吻合，一致)。
• 此外，HMM做了两个基本假设，HMM受限于这两个假设（字符\(c_t\)仅与前一字符\(c_{t−1}\)相关），而不能学习到更多的特征，泛化能力有限。
  • 齐次Markov性假设，即任意时刻\(t\)的状态仅与前一时刻状态相关，与其他时刻的状态、时刻\(t\)均无关；
  • 观测独立性假设，任意时刻t的观测仅依赖于该时刻HMM的状态，与其他的观测及状态均无关。

2-HMM

在上一篇中介绍了用HMM做中文分词，

• 对于未登录词（out-of-vocabulary, OOV）有良好的识别效果，
• 但是缺点也十分明显——对于词典中的（in-vocabulary, IV）词却未能很好地识别。

主要是因为，HMM本质上是一个Bigram(二元)的语法模型，未能深层次地考虑上下文（context）。对于此，本文将介绍更为复杂的二阶HMM。

预备知识

n-gram语法模型

n-gram语法模型用来：在已知前面\(n−1\)个词\(w_1, \cdots, w_{n-1}\)的情况下，预测下一个词出现的概率：

$P(w_n | w_1, \cdots, w_{n-1})$

常见的n-gram有:

• Unigram（一元）,当前词出现的概率为自身词频
• Bigram（二元）,当前词出现的概率只与前面一个词相关
• Trigram（三元），当前词出现的概率只与前面两个词相关

对应的计算公式如下：
\(\begin{align} \text{Unigram:} \quad & \hat{P} (w_3) = \frac{f(w_3)}{N} \cr \text{Bigram:} \quad & \hat{P} (w_3|w_2) = \frac{f(w_2, w_3)}{f(w_2)} \cr \text{Trigram:} \quad &\hat{P} (w_3|w_1,w_2) = \frac{f(w_1, w_2, w_3)}{f(w_1,w_2)} \ \end{align}\)
其中，\(N\)为语料中总词数，\(f(w_i)\)为词\(w_i\)在语料中出现的次数。

两种CWS模型

中文分词（Chinese word segmentation, CWS）的统计学习模型大致可以分为两类：

• Word-Based Generative Model
• Character-Based Discriminative Model

Word-Based Generative Model采用最大联合概率来对最佳分词方案建模，比如，对于句子\(c_1^{n}=c_1, \cdots, c_n\)，最佳分词\(w_1^m=w_1, \cdots, w_m\)应满足：

此模型可以简化为二阶Markov链（second order Markov Chain）——当前词的转移概率只与前两个词相关，即为Trigram语法模型：
\( \begin{equation} P(w_1^m) = \prod_{i=1}^{m}P(w_i|w_1^{i-1}) \approx \prod_{i=1}^{m}P(w_i|w_{i-2}^{i-1}) \end{equation} \)

Character-Based Discriminative Model采用类似与POS（Part-of-Speech,词性）那一套序列标注的方法来进行分词：

\(t_i\)表示字符\(c_i\)对应的B/M/E/S词标注。

HMM分词

根据贝叶斯定理，式(5)可改写为(个人：HMM是对联合概率建模，将联合概率建模成一个数据生成过程，然后根据贝叶斯定理求最大后验概率)：
\( \begin{aligned} \arg \mathop{\max}\limits_{t_1^n} P(t_1^n | c_1^n) & = \arg \mathop{\max}\limits_{t_1^n} \frac{P(c_1^n | t_1^n) P(t_1^n)}{P(c_1^n)} \\ & = \arg \mathop{\max}\limits_{t_1^n} P(c_1^n | t_1^n) P(t_1^n)\\ \end{aligned} \)
HMM做了两个基本假设：齐次Markov性假设与观测独立性假设，即

• 状态（标注）仅与前一状态相关:

$P(t_{i}|t_{1}^{i-1}) = P(t_i| t_{i-1})$

• 观测相互独立，即字符相对独立：

$P(c_1^n|t_1^n) = \prod_{i=1}^{n} P(c_i|t_1^n)$

• 观测值依赖于该时刻的状态，即字符的出现仅依赖于标注：

$P(c_i|t_1^n) = P(c_i | t_i)$

将上述三个等式代入下式：
\(\begin{aligned} P(c_1^n | t_1^n) P(t_1^n) & = \prod_{i=1}^{n} P(c_i|t_1^n) \times [P(t_n|t_{1}^{n-1}) \cdots P(t_i|t_{1}^{i-1}) \cdots P(t_2|t_1)] \\ & = \prod_{i=1}^{n} [P(c_i|t_i) \times P(t_i|t_{i-1})]\\ \end{aligned}\)

因此，用HMM求解式子(5)相当于

二阶HMM的状态转移依赖于其前两个状态，类似地，分词模型如下：

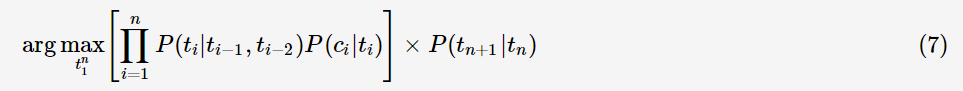
其中，\(t_{−1},t_0,t_{n+1}\)分别表示序列的开始标记与结束标记。

TnT

基于二阶HMM提出TnT (Trigrams'n'Tags) 序列标注方案，对条件概率\(P(t_3|t_2,t_1)\)采取了如下平滑（smooth）处理：

$P(t_3|t_2, t_1)=\lambda_1 \hat{P}(t_3) + \lambda_2 \hat{P}(t_3|t_2) + \lambda_3 \hat{P}(t_3|t_2, t_1)$

为了求解系数\(λ\)，TnT提出如下算法：

算法中，如果分母为0，则置式子的结果为0.

Character-Based Generative Model

鉴于两种CWS模型的利弊：

• Word-Based Generative Model高召回IV、低召回OOV；
• Character-Based Discriminative Model高召回OOV，低召回IV

结合两者提出了Character-Based Generative Model：

$\arg \mathop{\max}\limits_{t_1^n} P([c,t]_1^n)= \arg \mathop{\max}\limits_{t_1^n} \prod_{i=1}^n P([c,t]_i | [c,t]_{i-k}^{i-1})$

例子

isnowfy大神在项目Snownlp实现TnT与Character-Based Discriminative Model；并且在博文中给出了两者与最大匹配、Word-based Unigram模型的准确率比较，可以看出Generative Model的准确率较高。Snownlp的默认分词方案采用的是CharacterBasedGenerativeModel。

from snownlp import SnowNLP
s = SnowNLP('小明硕士毕业于中国科学院计算所，后在日本京都大学深造')
print('/'.join(s.words))
# 小明/硕士/毕业/于/中国/科学院/计算/所/，/后/在/日本/京都/大学/深造
# Jieba HMM: 小明/硕士/毕业于/中国/科学院/计算/所/，/后/在/日/本京/都/大学/深造

通过分析TnT、CharacterBasedGenerativeModel源码，发现作者在求解(7)、Generative Model的最大值都是采用穷举法，导致了较低的分词效率。此外，HanLP的作者hankcs大神给出了TnT算法的Java实现。

MEMM

MEMM是由McCallum et al. '2000 [1]提出MEMM，针对于HMM的两个痛点：

• 一是其为生成模型（generative model），
• 二是不能使用更加复杂的feature。

预备知识

概率图模型

概率图模型(probabilistic graphical model, PGM）指用图表示变量相关（依赖）关系的概率模型，主要分为两类：

• 有向图模型或贝叶斯网（Bayesian network），使用有向图表示变量间的依赖关系；
• 无向图模型或马尔可夫网（Markov network），使用无向图表示变量间相关关系。

监督学习的任务就是学习一个模型，对于给定的输入\(X\)，能预测出类别\(Y\)。
所学习到的模型一般可表示为决策函数：

或者为条件概率:

监督学习的模型分为生成模型（generative model）与判别模型（discriminative model）。

• 生成模型学习联合概率分布\(P(X,Y)\)，然后通过贝叶斯定理求解条件概率(2)，
• 而判别模型则是直接学习决策函数(1)或条件概率(2)。

HMM

HMM属于生成模型的有向图PGM，通过联合概率建模：

$P(S,O) = \prod_{t=1}^{n}P(s_t|s_{t-1})P(o_t|s_t)$

其中，\(S、O\)分别表示状态序列与观测序列。

HMM的解码问题为\(\arg \mathop{max}\limits_{S} P(S|O)\)；定义在时刻\(t\)状态为\(s\)的所有单个路径\(s^t_1\)中的概率最大值为

$\delta_t(s) = \max P(s_1^{t-1}, o_1^{t}, s_t=s)$

则有

$\begin{aligned} \delta_{t+1}(s) & = \max P(s_1^{t}, o_1^{t+1}, s_{t+1}=s) \\ & = \max_{s'} P(s_1^{t-1}, o_1^{t}, s_t=s') P(s_{t+1}|s_t) P(o_{t+1}|s_{t+1}) \\ & = \max_{s'} [\delta_t(s') P(s|s')] P(o_{t+1}|s) \end{aligned}$

上述式子即为（用于解决HMM的解码问题的）Viterbi算法的递推式；可以看出HMM是通过联合概率来求解标注问题的。

最大熵模型

最大熵（Maximum Entropy）模型属于log-linear model，在给定训练数据的条件下,对模型进行极大似然估计或正则化极大似然估计：

其中，

• \(Z_w(x) = \sum_{y} exp \left( \sum_i w_i f_i(x,y) \right)\)为归一化因子，
• \(w\)为最大熵模型的参数，
• \(f_i(x,y)\)为特征函数（feature function）——描述(x,y)的某一事实。最大熵模型并没有假定feature相互独立，允许用户根据domain knowledge设计feature。

最大熵马尔科夫模型

最大熵马尔科夫模型，即Max-Entropy Markov Models，在最大熵的基础上引入了一阶马尔科夫假设。它并没有像HMM通过联合概率建模，而是直接学习条件概率\(P(s_t|s_{t-1},o_t)\),因此，有别于HMM，MEMM的当前状态依赖于前一状态与当前观测；HMM与MEMM的图模型如下（左边为HMM，右边为MEMM）：

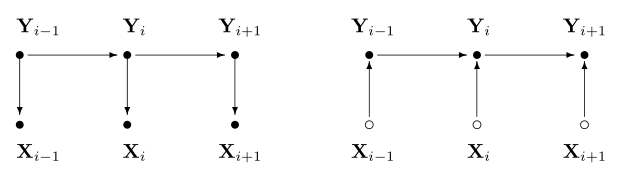
• MEMM属于判别模型，它要学习条件概率

  \(p(s_{1}...s_{m}|x_{1}...x_{m}) = \prod_{i=1}^{m}p(s_{i}|s_{1}...s_{i-1}, x_{1}...x_{m})\)
  这个等式主要根据条件概率的链式法则得到。

• 由于引入了一阶马尔科夫假设，故当前状态仅于前一状态有关
  \(p(s_{1}...s_{m}|x_{1}...x_{m}) = \prod_{i=1}^{m}p(s_{i}|s_{i-1}, x_{1}...x_{m})\)

• 对于上面等式右边连乘中的每一项条件概率，MEMM使用最大熵模型进行建模，而最大熵模型是对数线性模型，由上文可得到MEMM的条件概率表达式
  \(\begin{align*} p(s_{i}|s_{i-1}, x_{1}...x_{m}; \vec w) &= \frac{exp(\vec w \cdot \vec \phi (x_{1}...x_{m}, i, s_{i-1}, s_{i}))}{ \sum _{s{}' \epsilon S} exp(\vec w \cdot \vec \phi (x_{1}...x_{m}, i, s_{i-1}, s{}') ) } \\\\ & = \frac{1}{Z(s_{i-1},x_1,..,x_m)} exp(\vec w \cdot \vec \phi (x_{1}...x_{m}, i, s_{i-1}, s_{i})) \end{align*}\)
  \(\\\)
  \(\vec \phi (x_{1}...x_{m}, i, s_{i-1}, s{}')\)是\(i\)位置处的特征函数向量，维数为特征的个数，\(i\)代表当前被标记的位置,\(s_{i-1}\)代表先前的状态，\(s{}'\)代表当前的状态。

• 故有\(\begin{align*} p(s_{1}...s_{m}|x_{1}...x_{m}) &= \prod_{i=1}^{m} p(s_{i}|s_{i-1}, x_{1}...x_{m}) \\\\ &= \prod_{i=1}^{m}\frac{exp(\vec w\cdot \vec \phi (x_{1}...x_{m}, i, s_{i-1}, s_{i}))}{Z(s_{i-1},x_1,..,x_m)} \end{align*}\)

一旦我们已经定义好了特征向量\(\vec \phi\),那么我们就可以像在对数线性模型那里经常使用的方法一样，来得到MEMMs模型的参\(\vec w\).一旦我们经过训练，得到了模型的参数，那么我们将获得一个模型\(p(s_{i}|s_{i-1}, x_{1}...x_{m})\),并由此获得一个模型\(p(s_{1}...s_{m}|x_{1}...x_{m})\)。

Decoding with MEMMs
我们现在有一个新的测试句子\(x_1...x_m\)，我们的目标是计算这个测试句子最可能的状态序列，

$arg \underset{s_{1}...s_{m}}{max}\ p( s_{1}...s_{m}|x_{1}...x_{m})$ 我们将使用Viterbi算法来解决这个问题。

这里的Viterbi解码算法里面的关键数据结构是一个动态规划表\(\pi\)，里面的元素为\(\pi[j,s],j=1...m,s \epsilon S\),

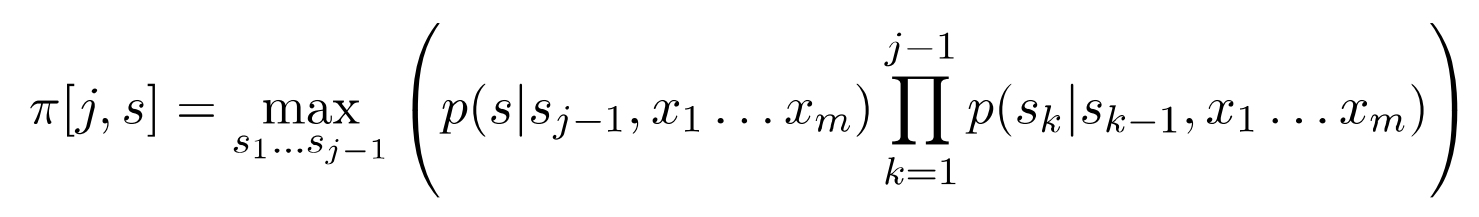
它存储的是任意在位置\(j\)以状态\(s\)结束的所有状态序列中最大的概率。
算法的具体流程如下：

• 初始化：对于任意的\(s \epsilon S\),
  
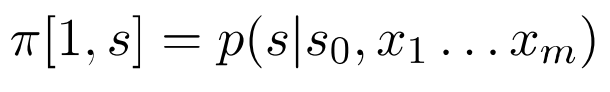
  这里的\(s_0\)是一个特殊的初始状态。
• for \(j= 2...m,s = 1...k\):
  
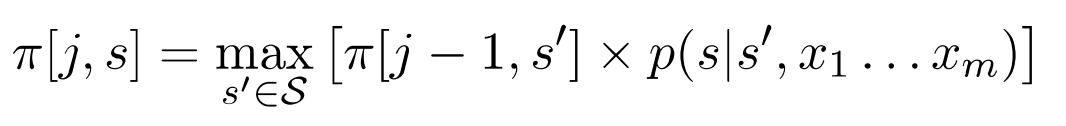
• 最后，我们可以计算得到
  
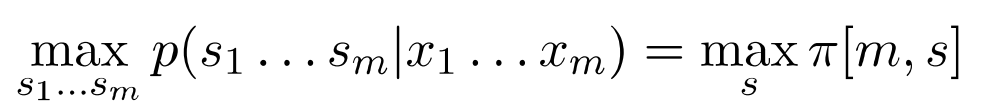
• 通过在动态规划中使用backpointers来得到最高分数的序列

纯暴力解码的话，复杂度为\(O(K^{m})\),通过Viterbi解码，我们可以把复杂度降到\(O(mK^{2})\) 。

MEMM缺陷

类似于HMM，MEMM的解码问题的递推式：

$\delta_{t+1}(s) = \max \limits_{s'} \delta_t(s') P(s|s', o_{t+1})$

但是，MEMM存在着标注偏置问题（label bias problem）。比如，有如下的概率分布：

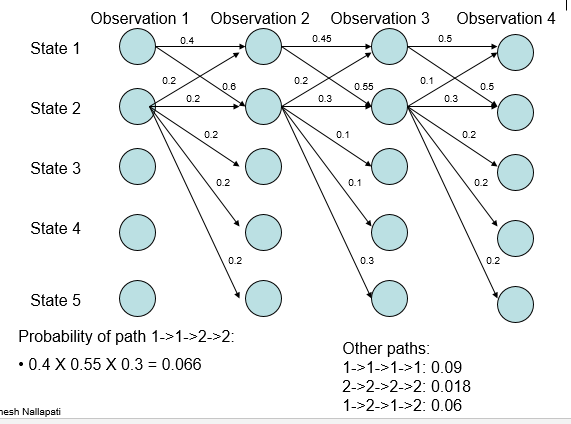
根据上述递推式，则概率最大路径如下：

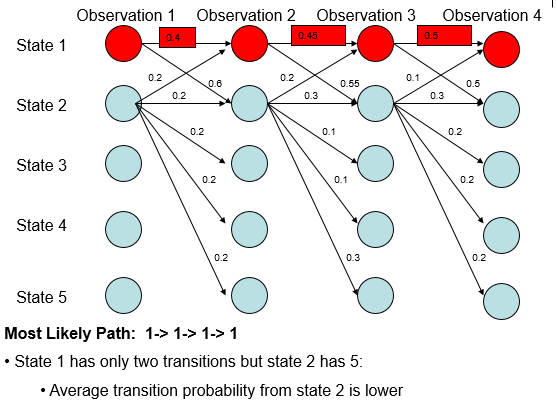
但是，从全局的角度分析：

• 无论观测值，State 1 总是更倾向于转移到State 2；
• 无论观测值，State 2 总是更倾向于转移到State 2.

上面得出的概率最大路径似乎和我们的直觉不符，是什么因素造成这种结果呢？从\(P(s|s',o)\)的建模公式可以看出，MEMM所做的是本地(局部)归一化，导致有更少转移的状态拥有的转移概率普遍偏高，MEMM的概率最大路径倾向于选择拥有更少转移的状态。因MEMM存在着标注偏置问题，故全局归一化的CRF被提了出来。

CRF

之前介绍的MMEM存在着label bias问题，因此Lafferty et al.提出了CRF (Conditional Random Field).

CRF是一种判别式模型，它的理论基础是逻辑回归。这里我们将从单样本二分类问题扩展到单样本多分类问题，最后延伸到序列样本多分类问题。

• 单样本二分类问题:在单样本二分类问题中使用逻辑回归，假设给定输入\(x\)，定义其分类概率为：
  
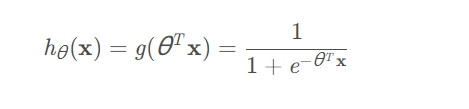
  该概率值的值域是\((0,1)\)，当输出概率值大于0.5时，我们将其归为正类；反之，将其分类负类。

• 单样本多分类问题: 在单样本多分类问题中使用softmax分类器，假设存在样本\(x\)，其被分成标签\(y=y^j\)的概率为：
  
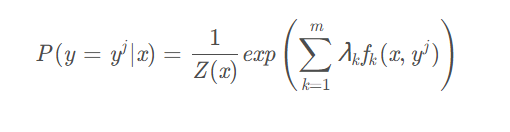
  其中\(f_k\)表示第\(k\)个特征函数,\(\lambda_k\)表示对应的权重，\(Z(x)\)是归一化因子，其值为:
  
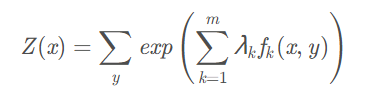
  其中\(y\)代表任意的分类类别。其实逻辑回归本质上也是一种softmax分类器，证明可见这里。

• 序列化样本多分类问题：条件随机场CRF是逻辑回归的一种扩展，将单样本多分类问题拓展到序列化样本多分类问题。
  
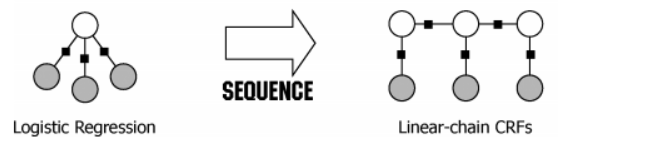
  它不像MEMM那样由一连串的分类器累积而成，而是直接将整个序列化分类当成一个整体的分类任务，进行全局的归一化。假设给定输入\(x_1^n\)，标签序列\(y_1^n\)的概率为:
  
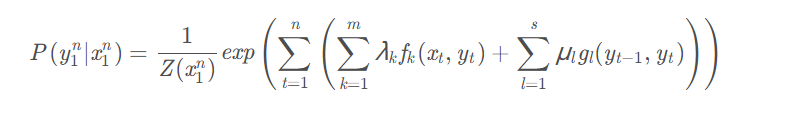
  其中\(f_k\)表示第\(k\)个状态特征函数，\(\lambda_k\)表示对应的权重；\(g_l\)表示第\(l\)个转移状态函数,\(\mu_l\)表示对应的权重值。\({Z(x_1^n)}\)是归一化因子，其值为:
  
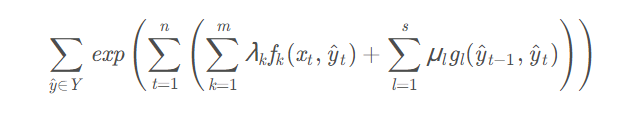
  其中\(Y\)表示所有可能的标签序列。有没有感觉CRF本质上就是一个softmax，只是它不是在单样本上面做的，而是序列化样本；为了保证是整个序列做的分类，在CRF中考虑了相邻状态之间的转换特征函数。