AUC小结

目录

前言

AUC是一个模型评价指标，只能用于二分类模型的评价，对于二分类模型，还有很多其他评价指标，比如logloss，accuracy，precision。如果你经常关注数据挖掘比赛，比如kaggle，那你会发现AUC和logloss基本上是最常见的模型评价指标。为什么AUC和logloss比accuracy更常用呢？

  • 因为很多机器学习的模型，对分类问题的预测结果都是概率，
  • 如果要计算accuracy，需要先把概率转化成类别，
  • 这就需要手动设置一个阈值，如果对一个样本的预测概率高于这个预测，就把这个样本放进一个类别里面，低于这个阈值，放进另一个类别里面。
  • 所以，这个阈值很大程度上影响了accuracy的计算。
  • 使用AUC或者logloss可以避免把预测概率转换成类别。

AUC是面试中经常问到的东西，也是一个非常经典和常用的评价指标，所以本文对AUC全面总结一下。

混淆矩阵

了解AUC之前，必须先了解混淆矩阵和ROC曲线。这里我们先介绍混淆矩阵的概念。混淆矩阵可以用来展示一个二分类器的预测结果，混淆矩阵中有着Positive(阳)、Negative(阴)、True(真)、False(伪)的概念，其意义如下：

  • 称预测类别为1的为Positive(阳性),预测类别为0的为Negative(阴性).
  • 预测正确的为True(真),预测错误的为False(伪).

对上述概念进行组合，就产生了如下的混淆矩阵：
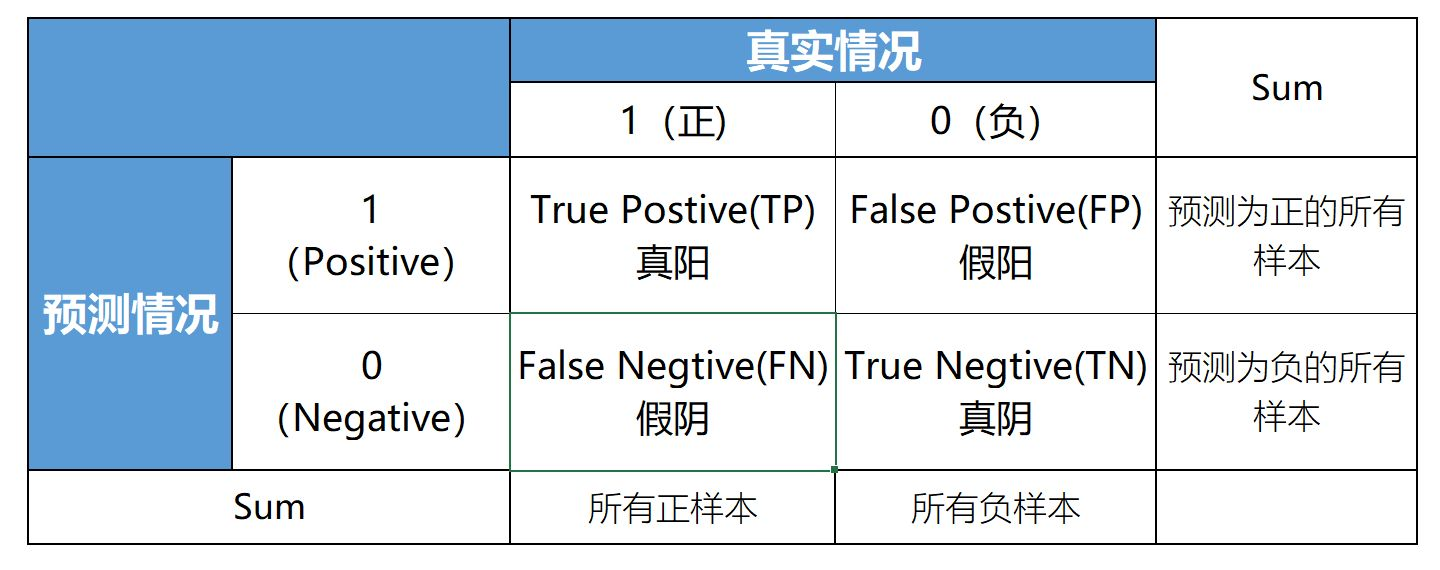
image
然后，由此引出True Positive Rate（真阳率）、False Positive（伪阳率）两个概念：

  • 真阳性率（True Positive Rate，随机取出一个正样本，预测它为正的概率）: \(TPR = \frac{TP}{TP+FN}\)(意义是在所有真实的正样本中，预测结果(预测分数是针对阳性而言的)为正的比例(分数)。当然是希望越大越好啦。熟悉召回率Recall的应该知道，这个公式也正是Recall的公式)
  • 假阳性率（False Positive Rate，随机取出一个负样本，预测它为正的概率）: \(FPR = \frac{FP}{FP+TN}\)(意义是在所有真实的负样本中，预测结果(预测分数是针对阳性而言的)为正的比例(分数)。当然是希望越小越好啦)

好了。对于AUC，混淆矩阵了解这么多就OK了。

ROC曲线

ROC曲线是Receiver Operating Characteristic Curve的简称，中文名是受试者工作特征曲线。
这一节主要来学如何绘制ROC曲线。

  • 首先，ROC曲线的横坐标是假阳性率FPR，纵坐标是真阳性率TPR。
  • 其次，明确计算AUC的时候，预测值y_pred一般都是[0, 1]的小数（代表预测为正样本的概率），真实值y_true为0或1。如果计算FPR和TPR，我们就需要知道预测的正负样本情况，但给的预测值是小数，如何划分预测的正负样本呢？答案是选取截断点。
  • 截断点是指区分正负预测结果的阈值。比如截断点=0.1，那就表示y_pred<0.1的为预测为负样本，y_pred>=0.1预测正样本。所以，绘制AUC曲线需要不断移动“截断点”来得到所有的(FPR，TPR)点，然后把这些点用线段连起来就是ROC曲线了。
  • 截断点取值为{正无穷，负无穷，预测值的所有唯一值}就够了。
    • 正无穷表示所有都预测为负样本，(fpr, tpr) = (0, 0)。
    • 负无穷表示所有都预测为正样本，(fpr, tpr) = (1, 1)。
    • 也就是这两个坐标点固定有，
    • 所以一般截断点默认取值就是预测值的所有唯一值(从大到小排列)。

如何绘制，如下图所示：
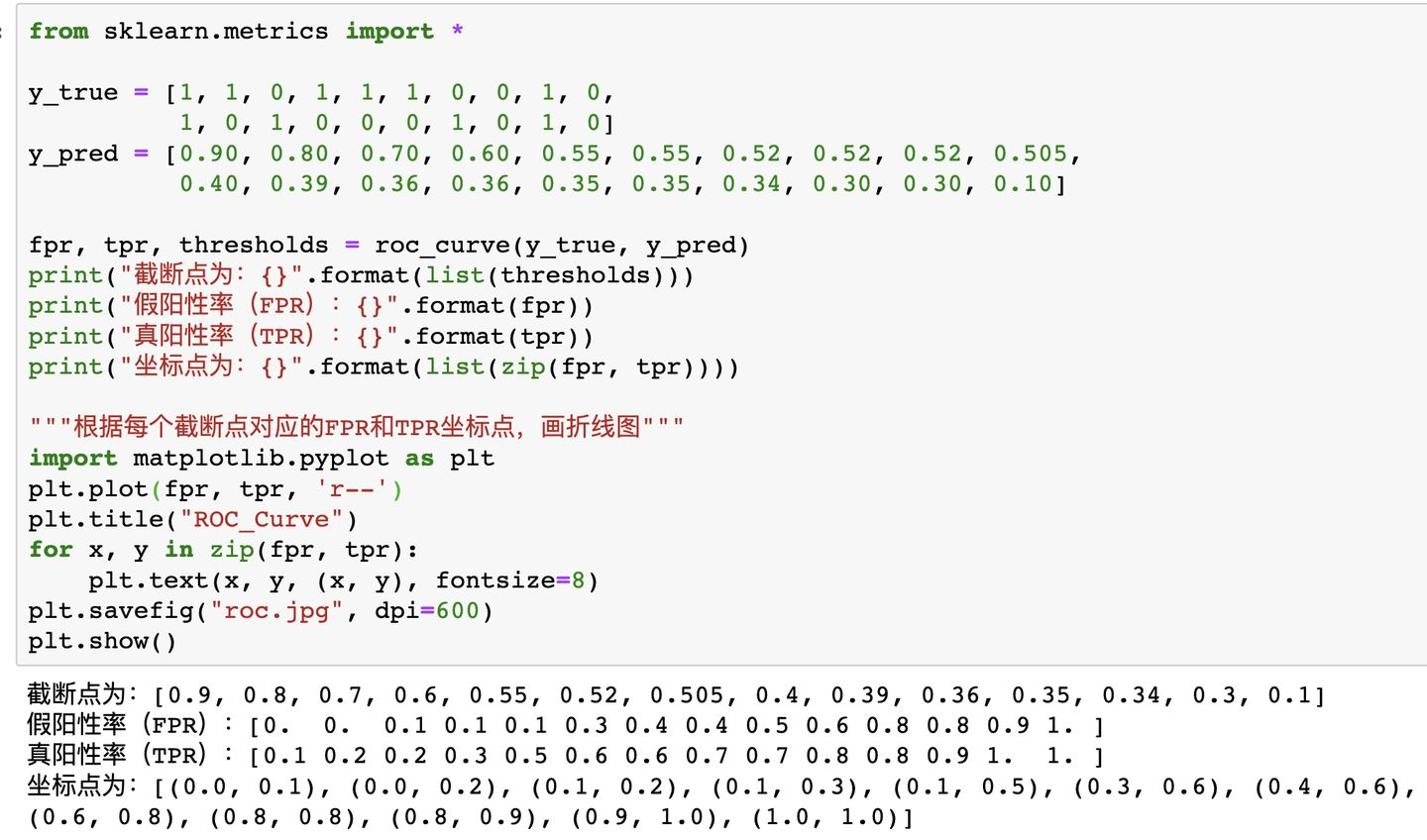
image

AUC定义

AUC（Area Under ROC Curve），顾名思义，即ROC曲线下的面积。AUC越大，说明分类器越可能把正样本排在前面，衡量的是一种排序的性能。

那么问题来了，ROC曲线下的面积怎么就能衡量分类器的排序能力？

如果ROC面积越大，说明曲线越往左上角靠过去。那么对于任意截断点，(FPR，TPR)坐标点越往左上角（0,1）靠，

  • 说明FPR较小趋于0（根据定义得知，就是在所有真实负样本中，基本没有预测为正的样本），
  • TRP较大趋于1（根据定义得知，也就是在所有真实正样本中，基本全都是预测为正的样本）。
  • 并且上述是对于任意截断点来说的，
  • 很明显，那就是分类器对正样本的打分基本要大于负样本的打分（一般预测值也叫打分），衡量的不就是排序能力嘛！

所以，现在可以给一个比较常用的AUC的定义。即：随机从正样本和负样本中各选一个，分类器对于该正样本打分大于该负样本打分的概率。

AUC计算

AUC如果按照原始定义ROC曲线下的面积来计算，非常之麻烦。可以转换一下思路，按照上述给出的常用的AUC定义，即:随机选出一对正负样本，分类器对于正样本打分大于负样本打分的概率。咱们就来算算这个概率到底是多少，那么也就算出AUC是多少了。
假设数据集一共有\(M\)个正样本，\(N\)个负样本，预测值也就是\(M+N\)个。我们将所有样本按照预测值进行从小到大排序，并排序编号由\(1\)到\(M+N\)。

  • 对于正样本概率最大的，假设排序编号为\(rank_1\)，比它概率小的负样本个数\(= rank_1 - M\)；
  • 对于正样本概率第二大的，假设排序编号为\(rank_2\)，比它概率小的负样本个数\(= rank_2 - (M-1)\)；
  • 以此类推。。。。。。
  • 对于正样本概率最小的,假设排序编号为\(rank_M\),比它概率小的负样本个数\(= rank_M - 1\)；

那么,在所有情况下，正样本打分大于负样本的对数等于：
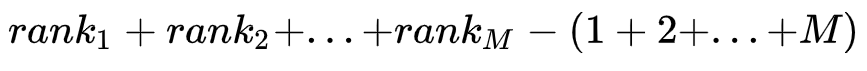
image
所以，AUC的正式计算公式(满足条件的对数/总对数)也就有了，如下:
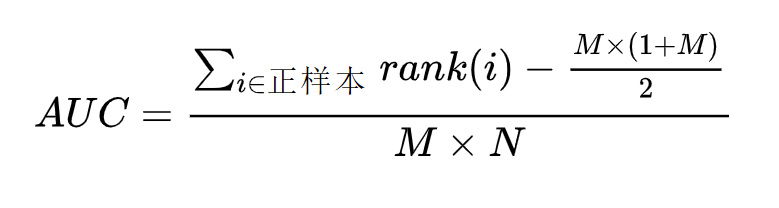
image
\(rank(i)\)表示正样本\(i\)的排序编号，\(M*N\)表示随机从正负样本各取一个的所有情况数。一般考代码题，比如用python写个AUC计算，也是用上述公式原理。

但是，还没有完，有一个小问题，可能大家没注意到。那就是如果有预测值是一样的，那么怎么进行排序编号呢？其实很简单，对于预测值一样的样本，我们将这些样本原先的排号平均一下，作为新的排序编号就完事了。仔细理解可看下图：
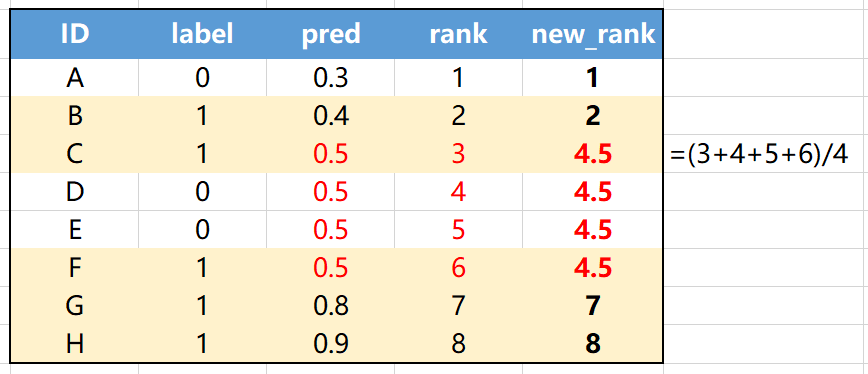
image
上图中，正样本个数M=5（黄底样本），负样本个数N=3（白底样本），预测值相同有4个（ID为CDEF）。我们将预测值pred相等的情况（上图红色字体），对其进行新的排序编号，变成(3+4+5+6)/4 = 4.5。
那么根据公式就可以算出上图的AUC等于：
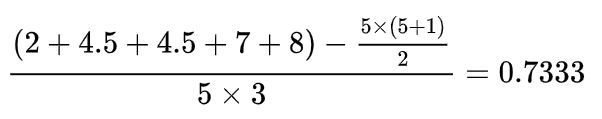
image
用sklearn的auc计算验证一下，一样。
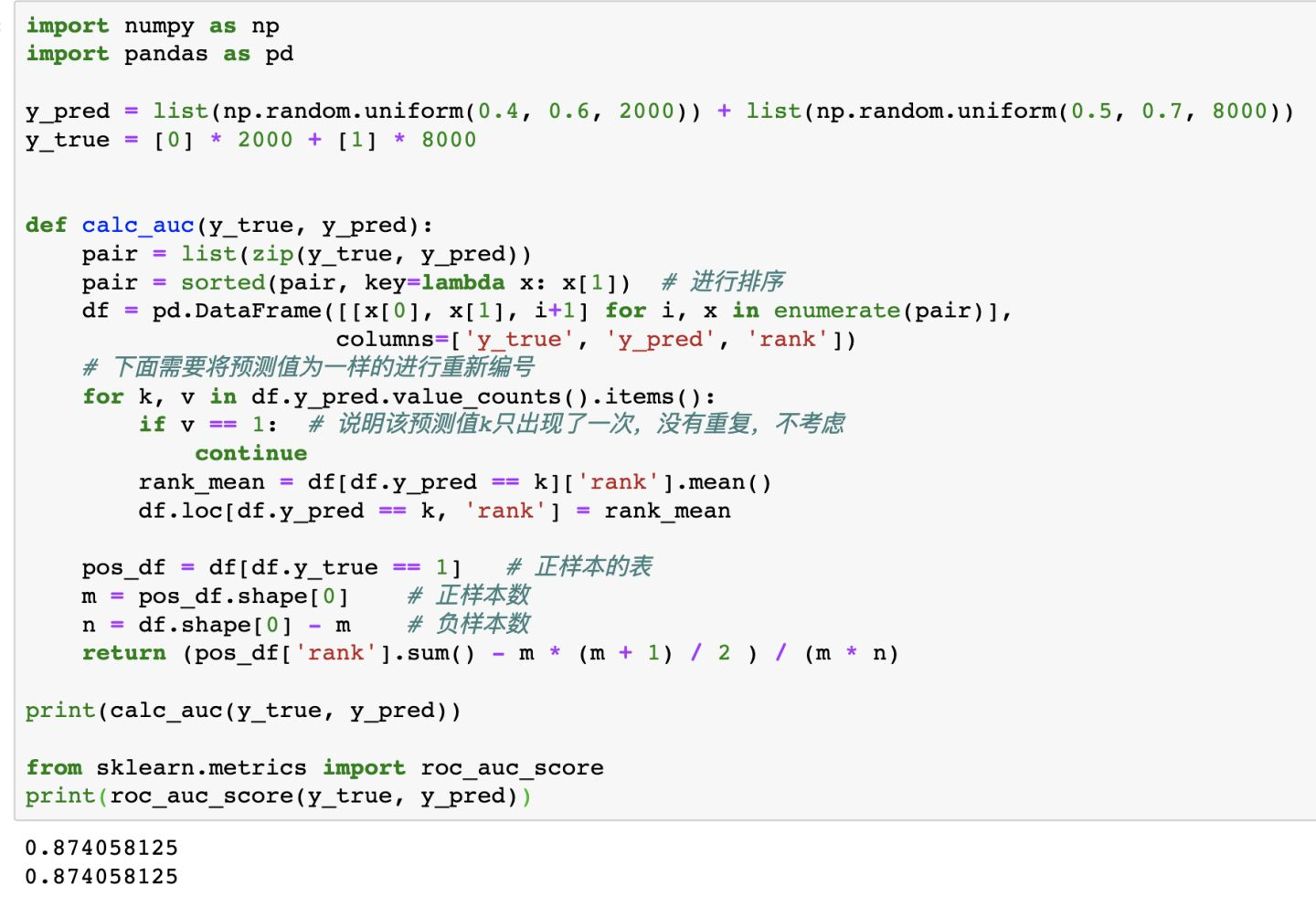
image

AUC的具体计算公式都给了，理解了其中逻辑，实现起来就比较容易了。代码如下，核心代码也就10行左右(个人：其实，我们可以使用transform操作处理预测值pred相等时的情况)：
image

总结

优点：

  • AUC衡量的是一种排序能力，因此特别适合排序类业务；
  • AUC对正负样本均衡并不敏感，在样本不均衡的情况下，也可以做出合理的评估。
  • 其他指标，比如precision，recall，F1，根据区分正负样本阈值的变化会有不同的结果，而AUC不需要手动设定阈值，是一种整体上的衡量方法。

缺点：

  • 忽略了预测的概率值和模型的拟合程度；
  • AUC反应了太过笼统的信息。无法反应召回率、精确率等在实际业务中经常关心的指标；
  • 它没有给出模型误差的空间分布信息，AUC只关注正负样本之间的排序，并不关心正样本内部，或者负样本内部的排序，这样我们也无法衡量模型对于好坏客户的好坏程度的刻画能力；

posted on 2022-03-18 15:43  朴素贝叶斯  阅读(820)  评论(0)  编辑  收藏  举报

导航