梯度提升树(GBDT)

目录

• 概述
• 梯度提升树(GBDT)
  • 负梯度拟合
  • GBDT回归算法
  • GBDT分类算法
  • GBDT常用损失函数
  • GBDT的正则化
• 小结

概述

GBDT有很多简称,有GBT(Gradient Boosting Tree),GTB(Gradient Tree Boosting， GBRT（Gradient Boosting Regression Tree）, MART(Multiple Additive Regression Tree)，其实都是指的同一种算法，本文统一简称GBDT。

梯度提升树(Gradient Boosting Decison Tree, 以下简称GBDT)是集成学习Boosting家族中的重要成员，但是却和传统的Adaboost有很大的不同:

• Adaboost，我们是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。

• GBDT也是迭代，使用了前向分步算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同。在GBDT的迭代中，假设我们前一轮迭代得到的强学习器是\(f_{t−1}(x)\)，损失函数是\(L(y,f_{t−1}(x))\)，我们本轮迭代的目标是找到一个CART回归树模型的弱学习器\(h_t(x)\)，让本轮的损失函数\(L(y,f_t(x))=L(y,f_{t−1}(x)+h_t(x))\)最小。也就是说，本轮迭代找到决策树，要让样本的损失尽量变得更小。

GBDT的思想可以用一个通俗的例子解释，假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。

从上面的例子看这个思想还是蛮简单的，但是有个问题是这个损失的拟合不好度量，损失函数各种各样，怎么找到一种通用的拟合方法呢？

梯度提升树(GBDT)

负梯度拟合

在上一节中，我们介绍了GBDT的基本思路，但是没有解决损失函数拟合方法的问题。针对这个问题，大牛Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树。第t轮的第i个样本的损失函数的负梯度表示为

\(r_{ti} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{t-1}\;\; (x)}\)

利用\((x_i,r_{ti})\;\; (i=1,2,..m)\),我们可以拟合一颗CART回归树，得到了第t颗回归树，其对应的叶节点区域

\(R_{tj}, j =1,2,..., J\)。其中J为叶子节点的个数。

针对每一个叶子节点里的样本，我们求出使损失函数最小，也就是拟合叶子节点最好的的输出值\(c_{tj}\)如下：

\(c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} L(y_i,f_{t-1}(x_i) +c)\)

这样我们就得到了本轮的决策树拟合函数如下：

\(h_t(x) = \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj})\)

从而本轮最终得到的强学习器的表达式如下：

\(f_{t}(x) = f_{t-1}(x) + \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj})\)

通过损失函数的负梯度来拟合，我们找到了一种通用的拟合损失误差的办法，这样无轮是分类问题还是回归问题，我们通过其损失函数的负梯度的拟合，就可以用GBDT来解决我们的分类回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。

GBDT回归算法

下面我们总结下GBDT的回归算法。为什么没有加上分类算法一起？那是因为分类算法的输出是不连续的类别值，需要一些处理才能使用负梯度，我们在下一节讲。

输入是训练集样本\(T={(x_1,y_1),(x_2,y_2),...(x_m,y_m)}\)，最大迭代次数T, 损失函数L。
输出是强学习器f(x)

• 1)初始化弱学习器
  \(f_0(x) = \underbrace{arg\; min}_{c}\sum\limits_{i=1}^{m}L(y_i, c)\)

• 2)对迭代轮数t=1,2,...T有：

  • a)对样本i=1,2，...m，计算负梯度
    \(r_{ti} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{t-1}\;\; (x)}\)
  • b)利用\((x_i,r_{ti})(i=1,2,..m)\), 拟合一颗CART回归树,得到第t颗回归树，其对应的叶子节点区域为\(R_{tj},j=1,2,...,J\)。其中J为回归树t的叶子节点的个数。
  • c)对叶子区域j =1,2,..J,计算最佳拟合值
    \(c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} L(y_i,f_{t-1}(x_i) +c)\)
  • d)更新强学习器
    \(f_{t}(x) = f_{t-1}(x) + \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj})\)

• 3)得到强学习器f(x)的表达式
  \(f(x) = f_T(x) =f_0(x) + \sum\limits_{t=1}^{T}\sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj})\)

GBDT分类算法

GBDT的分类算法从思想上和GBDT的回归算法没有区别，但是由于样本输出不是连续的值，而是离散的类别，导致我们无法直接从输出类别去拟合类别输出的误差。

为了解决这个问题，主要有两个方法，

• 一个是用指数损失函数，此时GBDT退化为Adaboost算法。

• 另一种方法是用类似于逻辑回归的对数似然损失函数的方法。也就是说，我们用的是类别的预测概率值和真实概率值的差来拟合损失。

本文仅讨论用对数似然损失函数的GBDT分类。而对于对数似然损失函数，我们又有二元分类和多元分类的区别。

二元GBDT分类算法:
对于二元GBDT，如果用类似于逻辑回归的对数似然损失函数，则损失函数为：
\(L(y, f(x)) = log(1+ exp(-yf(x)))\)
其中\(y∈\{−1,+1\}\)。则此时的负梯度误差为
\(r_{ti} = -\bigg[\frac{\partial L(y, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{t-1}\;\; (x)} = y_i/(1+exp(y_if(x_i)))\)
对于生成的决策树，我们各个叶子节点的最佳负梯度拟合值为
\(c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} log(1+exp(-y_i(f_{t-1}(x_i) +c)))\)
由于上式比较难优化，我们一般使用近似值代替
\(c_{tj} = \sum\limits_{x_i \in R_{tj}}r_{ti}\bigg / \sum\limits_{x_i \in R_{tj}}|r_{ti}|(1-|r_{ti}|)\)
除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，二元GBDT分类和GBDT回归算法过程相同。

多元GBDT分类算法:
多元GBDT要比二元GBDT复杂一些，对应的是多元逻辑回归和二元逻辑回归的复杂度差别。假设类别数为K，则此时我们的对数似然损失函数为：
\(L(y, f(x)) = - \sum\limits_{k=1}^{K}y_klog\;p_k(x)\)
其中如果样本输出类别为k，则\(y_k = 1\)。第k类的概率\(p_k(x)\)的表达式为：
\(p_k(x) = exp(f_k(x)) \bigg / \sum\limits_{l=1}^{K} exp(f_l(x))\)
集合上两式，我们可以计算出第t轮的第i个样本对应类别l的负梯度误差为
\(r_{til} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f_k(x) = f_{l, t-1}\;\; (x)} = y_{il} - p_{l, t-1}(x_i)\)
观察上式可以看出，其实这里的误差就是样本i对应类别l的真实概率和t−1轮预测概率的差值。
每一轮的训练实际上是训练了 K 棵树去拟合softmax的每一个分支模型的负梯度。
对于生成的决策树，我们各个叶子节点的最佳负梯度拟合值为
\(c_{tjl} = \underbrace{arg\; min}_{c_{jl}}\sum\limits_{i=0}^{m}\sum\limits_{k=1}^{K} L(y_k, f_{t-1, l}(x) + \sum\limits_{j=0}^{J}c_{jl} I(x_i \in R_{tjl}))\)
由于上式比较难优化，我们一般使用近似值代替
\(c_{tjl} = \frac{K-1}{K} \; \frac{\sum\limits_{x_i \in R_{tjl}}r_{til}}{\sum\limits_{x_i \in R_{til}}|r_{til}|(1-|r_{til}|)}\)
由于上式比较难优化，我们一般使用近似值代替
\(c_{tjl} = \frac{K-1}{K} \; \frac{\sum\limits_{x_i \in R_{tjl}}r_{til}}{\sum\limits_{x_i \in R_{til}}|r_{til}|(1-|r_{til}|)}\)

下图是Friedman在论文中对GBDT多分类给出的伪代码：

除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，多元GBDT分类和二元GBDT分类以及GBDT回归算法过程相同。

GBDT常用损失函数

这里我们再对常用的GBDT损失函数做一个总结。
对于分类算法，其损失函数一般有对数损失函数和指数损失函数两种:

• 如果是指数损失函数，则损失函数表达式为
  \(L(y, f(x)) = exp(-yf(x))\)
• 如果是对数损失函数，分为二元分类和多元分类两种,见上一节

对于回归算法，常用损失函数有如下4种:
均方误差(Mean Square Error，MSE):
这个是最常见的回归损失函数了
\(L(y, f(x)) =(y-f(x))^2\)
我们以 \(y-f(x)\) 为横坐标，MSE 为纵坐标，绘制其损失函数的图形：

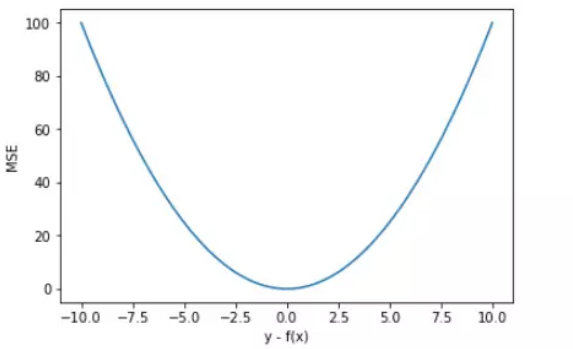
• MSE 曲线的特点是光滑连续、可导，便于使用梯度下降算法，是比较常用的一种损失函数。而且，MSE 随着误差的减小，梯度也在减小，这有利于函数的收敛，即使固定学习因子，函数也能较快取得最小值。

• 平方误差有个特性，就是当 \(y_i\) 与 \(f(x_i)\) 的差值大于 1 时，会增大其误差；当 \(y_i\) 与 \(f(x_i)\) 的差值小于 1 时，会减小其误差。这是由平方的特性决定的。也就是说， MSE 会对误差较大（>1）的情况给予更大的惩罚，对误差较小（<1）的情况给予更小的惩罚。从训练的角度来看，模型会更加偏向于惩罚较大的点，赋予其更大的权重。

• 如果样本中存在离群点，MSE 会给离群点赋予更高的权重，但是却是以牺牲其他正常数据点的预测效果为代价，这最终会降低模型的整体性能。

我们来看一下使用 MSE 解决含有离群点的回归模型。

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1, 20, 40)
y = x + [np.random.choice(4) for _ in range(40)]
y[-5:] -= 8
X = np.vstack((np.ones_like(x),x))    # 引入常数项 1
m = X.shape[1]
# 参数初始化
W = np.zeros((1,2))
 
# 迭代训练 
num_iter = 20
lr = 0.01
J = []
for i in range(num_iter):
   y_pred = W.dot(X)
   loss = 1/(2*m) * np.sum((y-y_pred)**2)
   J.append(loss)
   W = W + lr * 1/m * (y-y_pred).dot(X.T)
 
# 作图
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2])
plt.show()

拟合结果如下图所示：

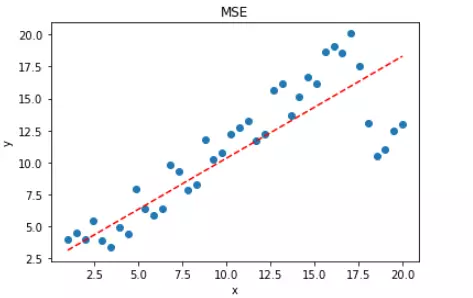
可见，使用 MSE 损失函数，受离群点的影响较大，虽然样本中只有 5 个离群点，但是拟合的直线还是比较偏向于离群点。这往往是我们不希望看到的。
平均绝对误差(Mean Absolute Error，MAE):
\(L(y, f(x)) =|y-f(x)|\)
对应负梯度误差为：\(sign(y_i-f(x_i))\)
以 y-f(x) 为横坐标，MAE 为纵坐标，绘制其损失函数的图形：

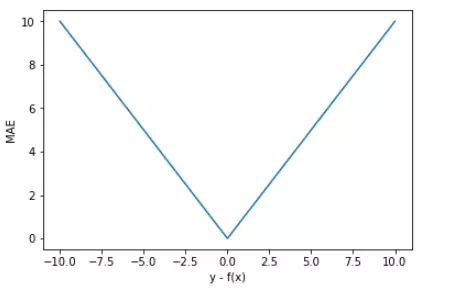
• 直观上来看，MAE 的曲线呈 V 字型，连续但在 y-f(x)=0 处不可导，计算机求解导数比较困难。而且 MAE 大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的。这不利于函数的收敛和模型的学习。

• 值得一提的是，MAE 相比 MSE 有个优点就是 MAE 对离群点不那么敏感，更有包容性。因为 MAE 计算的是误差 y-f(x) 的绝对值，无论是 y-f(x)>1 还是 y-f(x)<1，没有平方项的作用，惩罚力度都是一样的，所占权重一样。

针对 MSE 中的例子，我们来使用 MAE 进行求解，看下拟合直线有什么不同。

X = np.vstack((np.ones_like(x),x))    # 引入常数项 1
m = X.shape[1]
# 参数初始化
W = np.zeros((1,2))
 
# 迭代训练 
num_iter = 20
lr = 0.01
J = []
for i in range(num_iter):
   y_pred = W.dot(X)
   loss = 1/m * np.sum(np.abs(y-y_pred))
   J.append(loss)
   mask = (y-y_pred).copy()
   mask[y-y_pred > 0] = 1
   mask[mask <= 0] = -1
   W = W + lr * 1/m * mask.dot(X.T)
 
# 作图
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2],'r--')
plt.xlabel('x')
plt.ylabel('y')
plt.title('MAE')
plt.show()

拟合结果如下图所示：

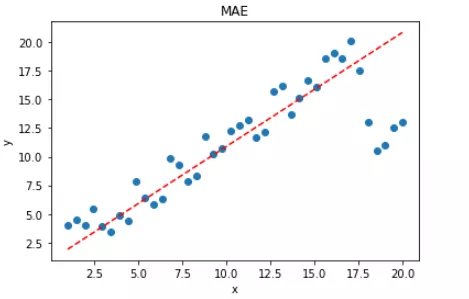
显然，使用 MAE 损失函数，受离群点的影响较小，拟合直线能够较好地表征正常数据的分布情况。这一点，MAE 要优于 MSE。二者的对比图如下：

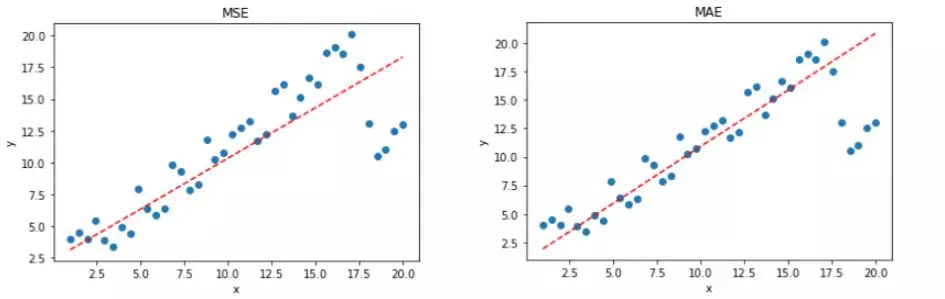
实际应用中，我们应该选择 MSE 还是 MAE 呢？

• 从计算机求解梯度的复杂度来说，MSE 要优于 MAE，而且梯度也是动态变化的，能较快准确达到收敛。

• 但是从离群点角度来看，如果离群点是实际数据或重要数据，而且是应该被检测到的异常值，那么我们应该使用MSE。

• 另一方面，离群点仅仅代表数据损坏或者错误采样，无须给予过多关注，那么我们应该选择MAE作为损失。

Huber损失:
它是均方差和绝对损失的折衷产物，对于远离中心的异常点，采用绝对损失，而中心附近的点采用均方差。这个界限一般用分位数点度量。损失函数如下：
\(L(y, f(x))= \begin{cases} \frac{1}{2}(y-f(x))^2& {|y-f(x)| \leq \delta}\\ \delta|y-f(x)| - \frac{1}{2}\delta^2& {|y-f(x)| > \delta} \end{cases}\)
对应的负梯度误差为：
\(r(y_i, f(x_i))= \begin{cases} y_i-f(x_i)& {|y_i-f(x_i)| \leq \delta}\\ \delta sign(y_i-f(x_i))& {|y_i-f(x_i)| > \delta} \end{cases}\)

• Huber Loss 是对MSE和MAE的综合，包含了一个超参数 δ。δ 值的大小决定了 Huber Loss 对 MSE 和 MAE 的侧重性，当 |y−f(x)| ≤ δ 时，变为 MSE；当 |y−f(x)| > δ 时，则变成类似于 MAE，因此 Huber Loss 同时具备了 MSE 和 MAE 的优点，减小了对离群点的敏感度问题，实现了处处可导的功能。

• Huber Loss 在 |y−f(x)| > δ 时，梯度一直近似为 δ，能够保证模型以一个较快的速度更新参数。当 |y−f(x)| ≤ δ 时，梯度逐渐减小，能够保证模型更精确地得到全局最优值。因此，Huber Loss 同时具备了前两种损失函数的优点。

通常来说，超参数 \(δ\) 可以通过交叉验证选取最佳值。下面，分别取 δ = 0.1、δ = 10，绘制相应的 Huber Loss，如下图所示：

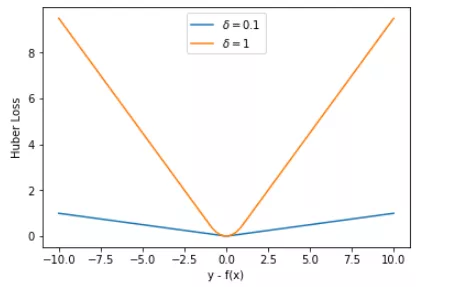
下面，我们用 Huber Loss 来解决同样的例子。

X = np.vstack((np.ones_like(x),x))    # 引入常数项 1
m = X.shape[1]
# 参数初始化
W = np.zeros((1,2))
 
# 迭代训练 
num_iter = 20
lr = 0.01
delta = 2
J = []
for i in range(num_iter):
   y_pred = W.dot(X)
   loss = 1/m * np.sum(np.abs(y-y_pred))
   J.append(loss)
   mask = (y-y_pred).copy()
   mask[y-y_pred > delta] = delta
   mask[mask < -delta] = -delta
   W = W + lr * 1/m * mask.dot(X.T)
 
# 作图
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2],'r--')
plt.xlabel('x')
plt.ylabel('y')
plt.title('MAE')
plt.show()

拟合结果如下图所示：

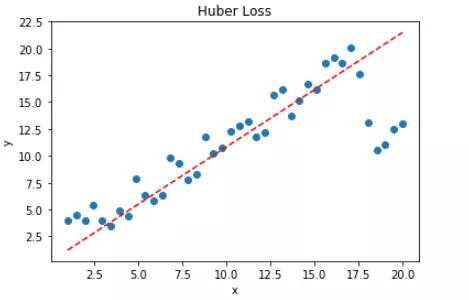
可见，使用 Huber Loss 作为损失函数，对离群点仍然有很好的抗干扰性，这一点比 MSE 强。另外，我们把这三种损失函数对应的 Loss 随着迭代次数变化的趋势绘制出来：

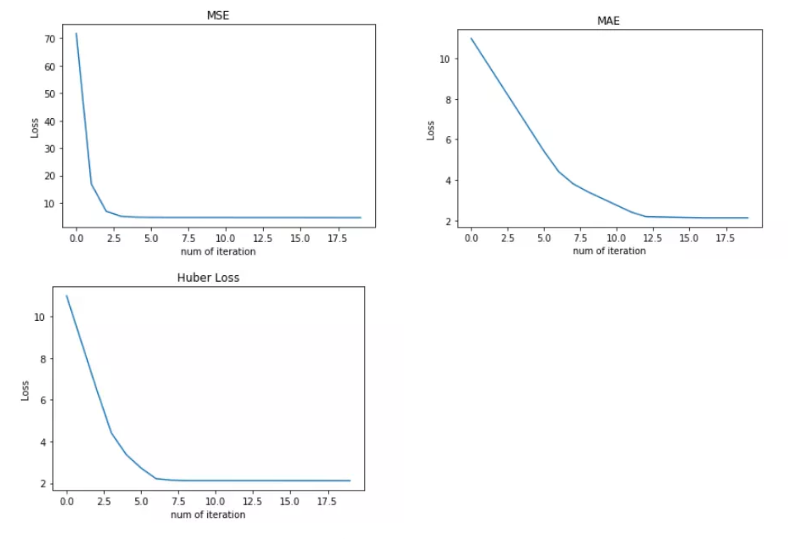
对比发现，MSE 的 Loss 下降得最快，MAE 的 Loss 下降得最慢，Huber Loss 下降速度介于 MSE 和 MAE 之间。也就是说，Huber Loss 弥补了此例中 MAE 的 Loss 下降速度慢的问题，使得优化速度接近 MSE。
最后，我们把以上介绍的回归问题中的三种损失函数全部绘制在一张图上。

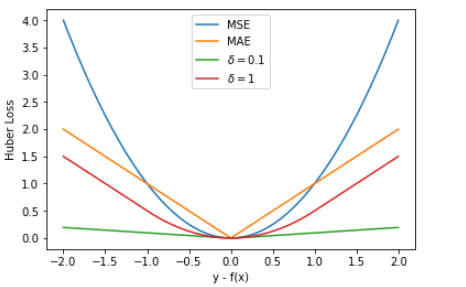
分位数损失。它对应的是分位数回归的损失函数，表达式为
\(L(y, f(x)) =\sum\limits_{y \geq f(x)}\theta|y - f(x)| + \sum\limits_{y < f(x)}(1-\theta)|y - f(x)|\)
其中\(θ\)为分位数，需要我们在回归前指定。对应的负梯度误差为：
\(r(y_i, f(x_i))= \begin{cases} \theta& { y_i \geq f(x_i)}\\ \theta - 1 & {y_i < f(x_i) } \end{cases}\)

对于Huber损失和分位数损失，主要用于健壮回归，也就是减少异常点对损失函数的影响。

GBDT的正则化

和Adaboost一样，我们也需要对GBDT进行正则化，防止过拟合。GBDT的正则化主要有三种方式。

• 第一种是和Adaboost类似的正则化项，即步长(learning rate)。定义为\(ν\),对于前面的弱学习器的迭代
  \(f_{k}(x) = f_{k-1}(x) + h_k(x)\)
  如果我们加上了正则化项，则有
  \(f_{k}(x) = f_{k-1}(x) + \nu h_k(x)\)
  \(ν\) 的取值范围为\(0<ν≤1\)。对于同样的训练集学习效果，较小的ν意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。

• 第二种正则化的方式是通过子采样比例（subsample）。取值为(0,1]。注意这里的子采样和随机森林不一样，随机森林使用的是放回抽样，而这里是不放回抽样。如果取值为1，则全部样本都使用，等于没有使用子采样。如果取值小于1，则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低。推荐在[0.5, 0.8]之间。
  使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样，程序可以通过采样分发到不同的任务去做boosting的迭代过程，最后形成新树，从而减少弱学习器难以并行学习的弱点。

• 第三种是对于弱学习器即CART回归树进行正则化剪枝。

小结

最后总结下GBDT的优缺点。
GBDT主要的优点有：

• 可以灵活处理各种类型的数据，包括连续值和离散值。

• 在相对少的调参时间情况下，预测的准确率也可以比较高。这个是相对SVM来说的。

• 使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。

GBDT的主要缺点有：

• 由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。

参考：
深入理解GBDT多分类算法
梯度提升树(GBDT)原理小结
[损失函数] MSE, MAE, Huber loss详解