Gradient Boosting Tree算法原理
基础知识
最优化方法
梯度下降法(Gradient descend method)
在机器学习任务中,需要最小化损失函数\(L(\theta)\), 其中\(\theta\)是要求解的模型参数。 梯度下降法常用来求解这种无约束最优化问题, 它是一种迭代方法:选取初值 \(\theta^0\),不断迭代,更新 \(\theta\) 的值,进行损失函数的极小化。
- 迭代公式:\(\theta^t = \theta^{t-1} + \Delta \theta\)
- 将\(L(\theta)\)在\(\theta^{t-1}\)处进行一阶泰勒展开:
\(\begin{align*} L(\theta^t) & = L(\theta^{t-1} + \Delta \theta) \\& \approx L(\theta^{t-1}) + L^{'}(\theta^{t-1})\Delta \theta \end{align*}\) - 要使\(L(\theta^t) < L(\theta^{t-1})\),可取:\(\Delta \theta = -\alpha L^{'}(\theta^{t-1})\),则\(\theta^t = \theta^{t-1} - \alpha L^{'}(\theta^{t-1})\)
这里\(\alpha\)是步长,可通过line search确定, 但一般直接赋一个小的数。
牛顿法(Newton's Method)
- 将\(L(\theta^t)\)在\(\theta^t\)处进行二阶泰勒展开:
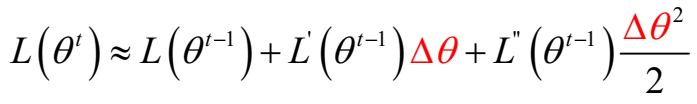
为了简化分析过程,假设参数是标量(即\(\theta\) 只有一维),则可将一阶和二阶导数分别记为 \(g\) 和 \(h\):
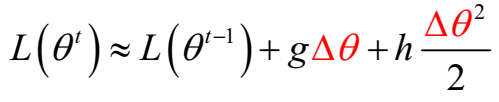
- 要使得\(L(\theta^t)\)极小,即让\(g\Delta \theta + h\frac{\Delta \theta^2}{2}\)极小,可令:
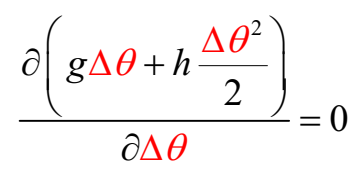
可得:\(\Delta \theta = - \frac{g}{h}\),故
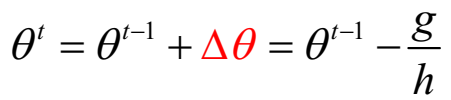
参数 \(\theta\) 推广到向量形式,迭代公式为:\(\theta^t = \theta^{t-1} - H^{-1}g\),这里\(H\)是海森矩阵。
从参数空间到函数空间
- GBDT 在函数空间中利用梯度下降法进行优化
- XGBoost 在函数空间中用牛顿法进行优化
注:实际上GBDT泛指所有梯度提升树算法,包括XGBoost,它也是GBDT的一种变种,这里为了区分它们,GBDT特指“ Greedy Function Approximation: A Gradient Boosting Machine” 里提出的算法,它只用了一阶导数信息。
Boosting算法是一种加法模型(additive training),
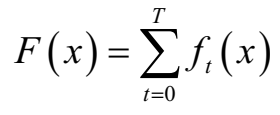
基分类器 \(f\) 常采用回归树[Friedman 1999]和逻辑回归[Friedman 2000]。 下文以回归树展开介绍。
树模型有以下优缺点:
优点:
- 可解释性强
- 可处理混合类型特征
- 具体伸缩不变性(不用归一化特征)
- 有特征组合的作用
- 可自然地处理缺失值
- 对异常点鲁棒
- 有特征选择作用
- 可扩展性强,容易并行
缺点:
- 缺乏平滑性(回归预测时输出值只能输出有限的若干种数值)
- 不适合处理高维稀疏数据
从Gradient Descend 到 Gradient Boosting:
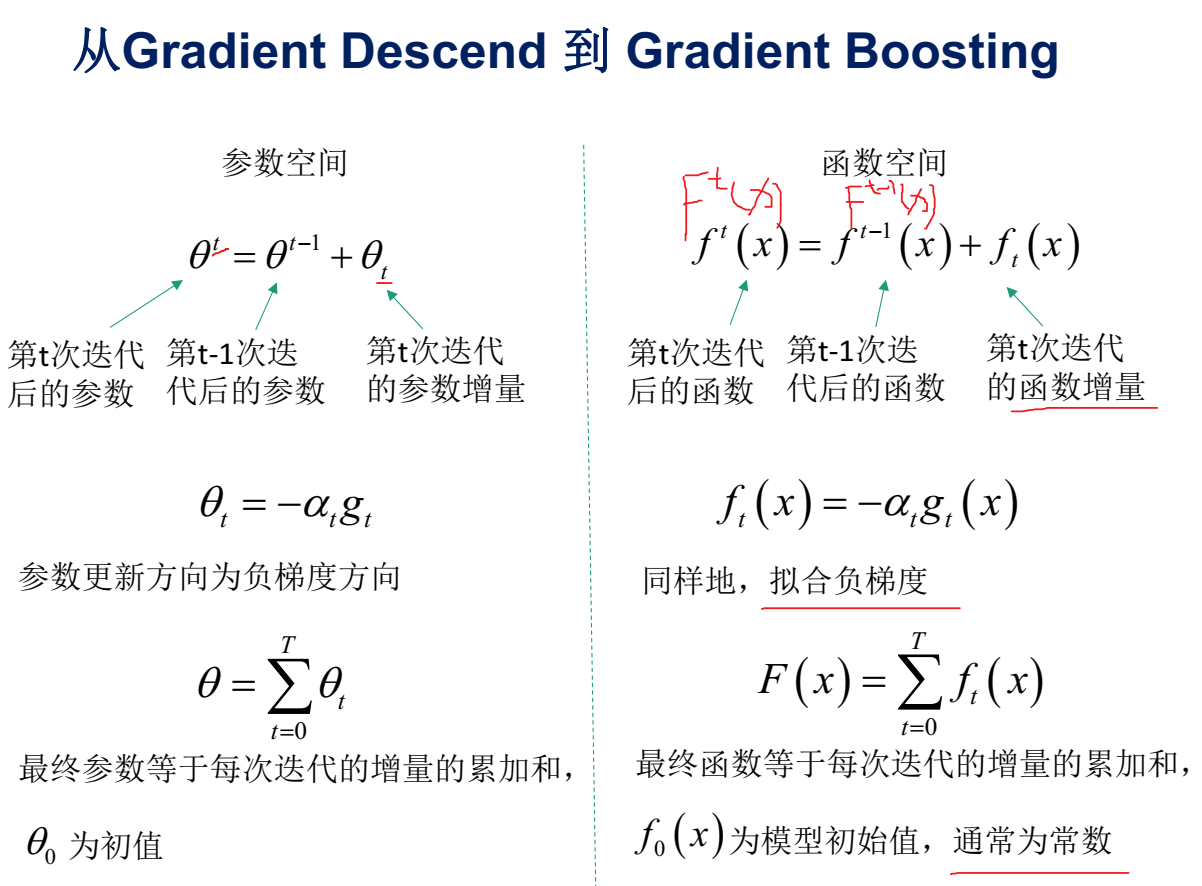
从Newton's Method 到 Newton Boosting:

Gradient Boosting Tree算法
Friedman于论文"Greedy Function Approximation:A Gradient Boosting Machine"中最早提出GBDT,其模型\(F\)定义为加法模型:
\(F(x;w) = \sum\limits_{t=0}^T \alpha_th_t(x;w_t) = \sum\limits_{t=0}^T f_t(x;w_t)\)
其中,\(x\)为输入样本,\(h\)为分类回归树,\(w\)是分类回归树的参数,\(\alpha\)是每棵树的权重。
通过最小化损失函数求解最优模型:
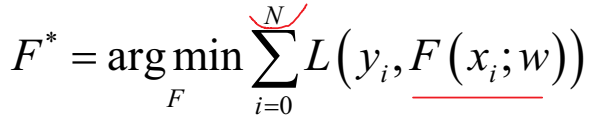
这是一个NP难问题,我们一般通过贪心法,迭代求局部最优解。


