LSTM、GRU网络详解

LSTM

长短期记忆网络（Long Short-Term Memory Network，LSTM[Gers et al.,2000; Hochreiter et al., 1997]是循环神经网络的一个变体，可以有效地解决简单循环神经网络的梯度爆炸或消失问题．
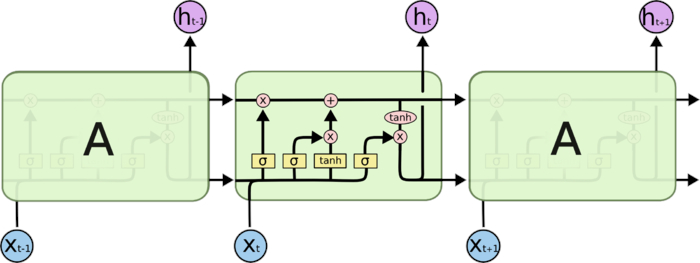
image
LSTM网络主要改进在以下两个方面：

  • 新的内部状态
    LSTM网络引入一个新的内部状态(internal state) \(𝒄_𝑡∈ℝ^𝐷\)

    • 专门进行线性的循环信息传递，
    • 同时(非线性地)输出信息给隐藏层的外部状态\(𝒉_t ∈ ℝ^𝐷\)(个人：最后的外部状态\(𝒉_t\)是从内部状态\(c_t\)中非线性输出的)．

  • 门控机制
    在数字电路中，门(gate)为一个二值变量{0, 1}，0代表关闭状态,不许任何信息通过；1代表开放状态，允许所有信息通过．
    LSTM网络引入门控机制(Gating Mechanism)来控制信息传递的路径．LSTM网络中的“门”是一种“软”门，取值在(0, 1)之间， 表示以一定的比例允许信息通过．
    (1) 遗忘门\(𝒇_𝑡\) 控制上一个时刻的内部状态\(𝒄_{𝑡−1}\)需要遗忘多少信息(个人：其实遗忘门是需要记住上一颗时刻内部状态的多少信息)
    (2) 输入门\(𝒊_𝑡\) 控制当前时刻的候选状态\(\tilde{c}_t\)有多少信息需要保存
    (3) 输出门\(𝒐_𝑡\) 控制当前时刻的内部状态 \(𝒄_𝑡\) 有多少信息需要输出给外部状态\(𝒉_𝑡\)

图6.7给出了LSTM网络的循环单元结构，其计算过程为：

  • 1） 首先利用上一时刻的外部状态\(𝒉_{𝑡−1}\)和当前时刻的输入\(𝒙_𝑡\)，计算出三个门，以及候选状态\(\tilde{c}_t\)
  • 2） 结合遗忘门\(𝒇_𝑡\)和输入门\(𝒊_𝑡\)来更新记忆单元\(𝒄_𝑡\)
  • 3） 结合输出门\(𝒐_𝑡\)，将内部状态的信息传递给外部状态\(𝒉_𝑡\)

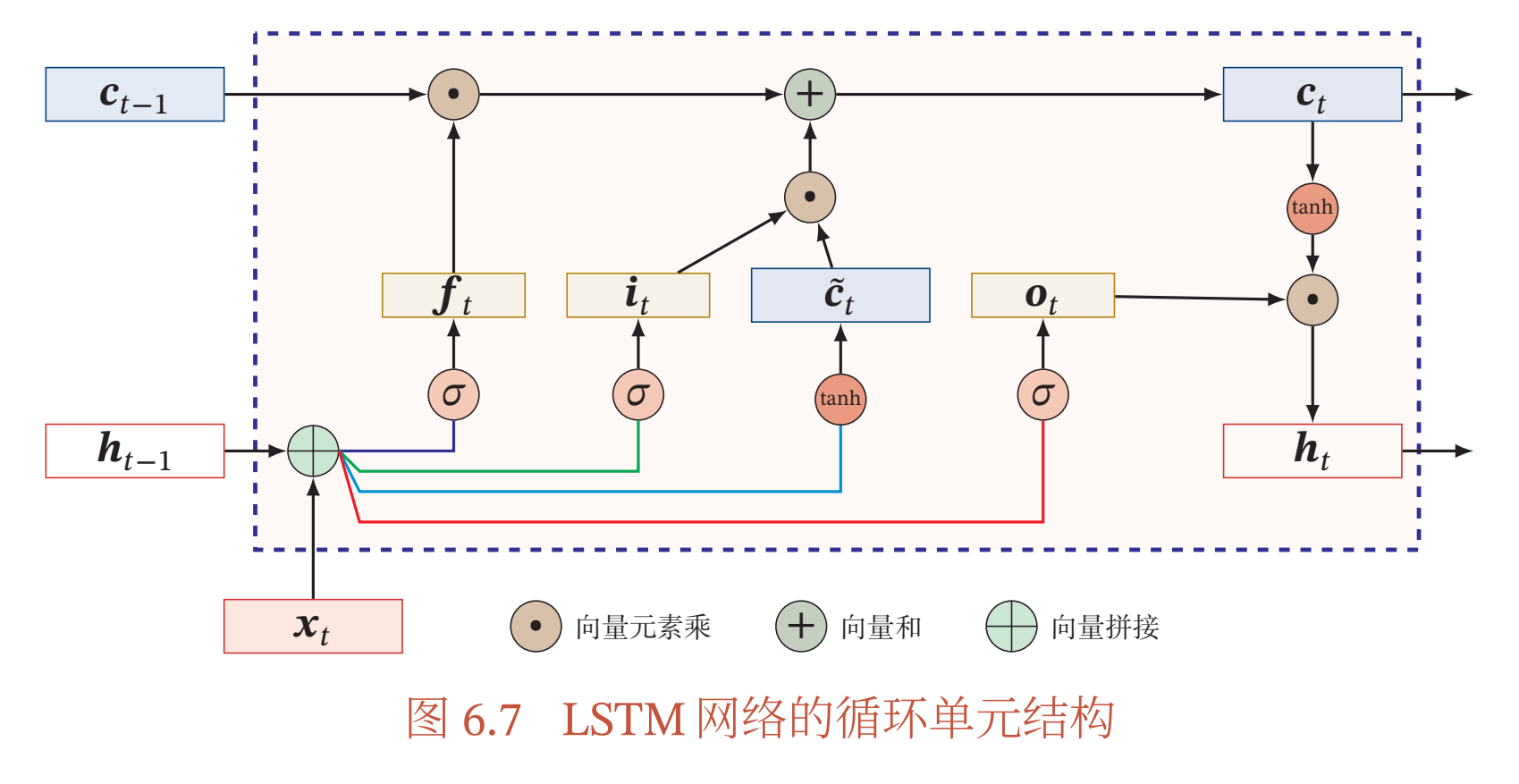
image

具体的计算公式为：

  • 遗忘门\(f_t\)： \(f_t=\sigma(W_fx_t + U_f h_{t-1} + b_f)\)
  • 输入门\(i_t\)： \(i_t=\sigma(W_ix_t + U_i h_{t-1} + b_i)\)
  • 输出门\(o_t\)： \(o_t=\sigma(W_ox_t + U_o h_{t-1} + b_o)\)
  • 候选状态\(\tilde{c}_t\)：\(\tilde{c}_t=\tanh(W_c x_t + U_c h_{t-1}+b_c)\)
  • 记忆单元\(𝒄_𝑡\)：\(c_t=f_t \odot c_{t-1} + i_t \odot \tilde{c}_t\)
    当\(f_t = 0, i_t = 1\)时，记忆单元将历史信息清空，并将候选状态向量\(\tilde{c}_t\)写入．但此时记忆单元\(𝒄_𝑡\)依然和上一时刻的历史信息相关．当\(𝒇_𝑡 = 1, 𝒊_𝑡 = 0\) 时，记忆单元将复制上一时刻的内容，不写入新的信息．
  • 隐含层输出外部状态\(𝒉_𝑡\)：\(h_t=o_t \odot \tanh(c_t)\)

通过LSTM循环单元，整个网络可以建立较长距离的时序依赖关系．上面的公式可以简洁地描述为：
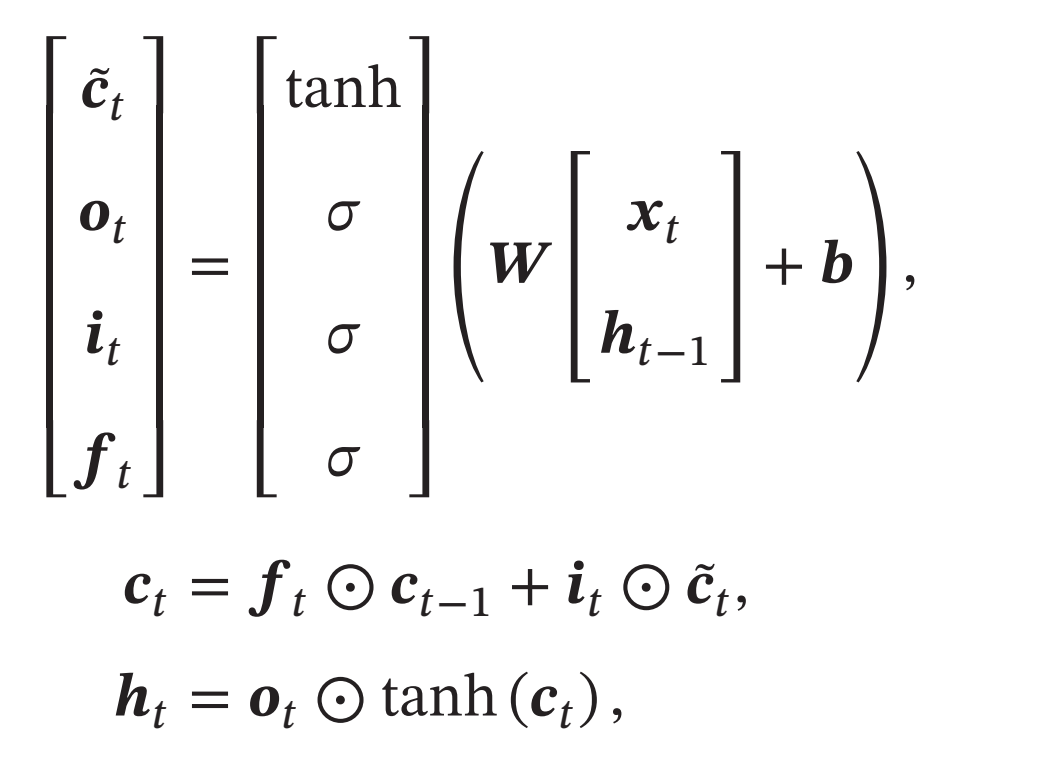
image
其中\(𝒙_𝑡∈ℝ^𝑀\)为当前时刻的输入，\(𝑾∈ℝ^{4𝐷×(𝑀+𝐷)}\)和\(𝒃∈ℝ^{4𝐷}\)为网络参数。

注：

  • LSTM名称的由来

    • 循环神经网络中的隐状态𝒉存储了历史信息，可以看作一种记忆(Memory)．在简单循环网络中，隐状态每个时刻都会被重写，因此可以看作一种短期记忆(Short-Term Memory)．
    • 在神经网络中，长期记忆(Long-Term Memory)可以看作网络参数，隐含了从训练数据中学到的经验，其更新周期要远远慢于短期记忆．
    • 而在LSTM网络中,记忆单元𝒄可以在某个时刻捕捉到某个关键信息,并有能力将此关键信息保存一定的时间间隔(个人：遗忘门)。记忆单元𝒄中保存信息的生命周期要长于短期记忆𝒉,但又远远短于长期记忆,因此称为长短期记忆(Long Short-Term Memory).长短期记忆是指长的“短期记忆”．

  • LSTM网络参数的初始化
    一般在深度网络参数学习时，参数初始化的值一般都比较小．但是在训练LSTM网络时，过小的值会使得遗忘门的值比较小．这意味着前一时刻的信息大部分都丢失了，这样网络很难捕捉到长距离的依赖信息．并且相邻时间间隔的梯度会非常小，这会导致梯度弥散问题．因此遗忘的参数初始值一般都设得比较大，其偏置向量\(𝒃_𝑓\)设为1或2．

GRU

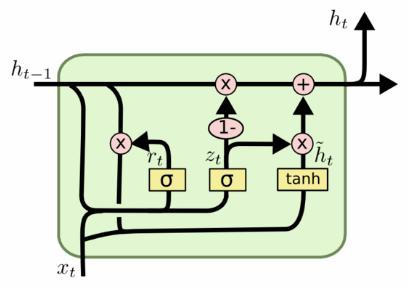
image

门控循环单元(Gated Recurrent Unit，GRU)网络[Cho et al., 2014; Chung et al.,2014]是一种比LSTM网络更加简单的循环神经网络.
图6.8给出了GRU网络的循环单元结构.
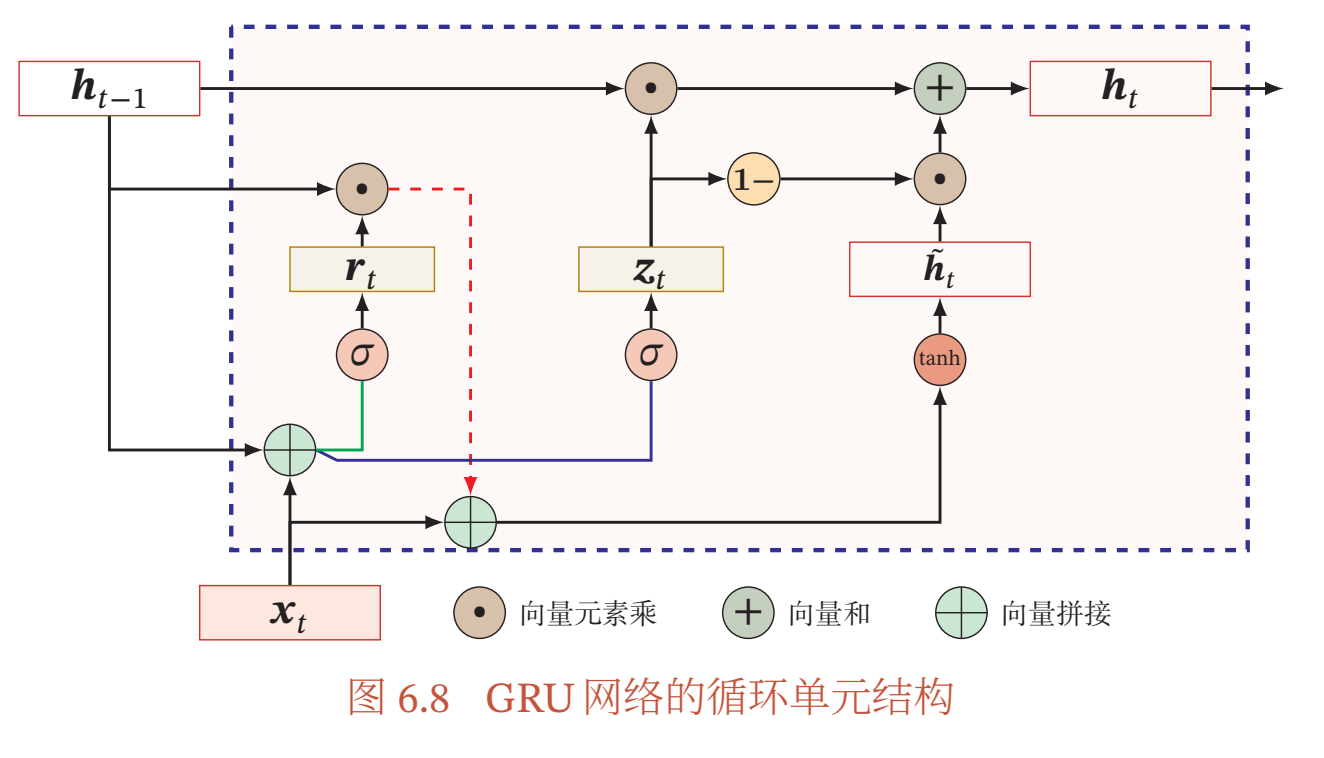
image

GRU网络引入门控机制来控制信息更新的方式.和LSTM不同，GRU不引入额外的记忆单元，

  • 更新门(Update Gate)\(z_t\)(个人：也就是那个比例系数) :控制当前状态需要从历史状态中保留多少信息(不经过非线性变换),以及需要从候选状态中接受多少新信息.在LSTM网络中，输入门和遗忘门是互补关系，具有一定的冗余性．GRU网络直接使用一个门\(z_t\)来控制输入和遗忘之间的平衡．
  • 重置门(Reset Gate)\(r_t\)(个人：计算候选状态时，对上一个时候状态的重置比例系数):用来控制候选状态\(\tilde{h}_t\)的计算是否依赖上一时刻的状态\(𝒉_{𝑡−1}\)．

计算公式：

  • 更新门\(z_t\)：\(z_t = \sigma(W_zx_t+U_zh_{t-1}+b_z)\),\(𝒛_𝑡 ∈ [0, 1]^𝐷\)
    当\(𝒛_𝑡=0\)时,当前状态\(𝒉_𝑡\)和前一时刻的状态\(𝒉_{𝑡−1}\)之间为非线性函数关系;当\(𝒛_𝑡=1\)时，\(𝒉_𝑡\)和\(𝒉_{𝑡−1}\)之间为线性函数关系
  • 重置门\(r_t\):\(r_t=\sigma(W_rx_t+U_rh_{t-1}+b_r)\),\(𝒓_𝑡 ∈ [0, 1]^𝐷\)
  • 候选状态\(\tilde{h}_t\):\(\tilde{h}_t=\tanh(W_hx_t+U_h(r_t \odot h_{t-1}) + b_h)\)
    当\(𝒓_𝑡 = 0\)时,候选状态\(\tilde{h}_t = \tanh(𝑾_𝑐𝒙_𝑡 + 𝒃)\)只和当前输入\(𝒙_𝑡\)相关,和历史状态无关.当\(𝒓_𝑡 = 1\)时,候选状态\(\tilde{h}_t = \tanh(𝑾_ℎ𝒙_𝑡 + 𝑼_ℎ𝒉_{𝑡−1} + 𝒃_ℎ)\)和当前输入\(𝒙_𝑡\)以及历史状态\(𝒉_{𝑡−1}\)相关,和简单循环网络一致
  • 隐藏状态\(h_t\)：\(h_t=z_t \odot h_{t-1} + (1-z_t) \odot \tilde{h}_t\)
    可以看出,当\(𝒛_𝑡 = 0, 𝒓_t = 1\)时,GRU网络退化为简单循环网络;若\(𝒛_𝑡 = 0, 𝒓_t = 0\)时， 当前状态\(𝒉_𝑡\)只和当前输入\(𝒙_𝑡\)相关,和历史状态\(𝒉_{𝑡−1}\)无关.当\(𝒛_𝑡 = 1\)时,当前状态\(𝒉_𝑡 = 𝒉_{𝑡−1}\)等于上一时刻状态\(𝒉_{𝑡−1}\),和当前输入\(𝒙_𝑡\)无关

posted on 2021-04-09 20:49  朴素贝叶斯  阅读(2191)  评论(0)  编辑  收藏  举报

导航