LogSumExp
机器学习中有很多巧妙的窍门,
- 可以加速训练
- 提升表现
- ...
今天我将讨论LogSumExp这一机器学习中常见的模式。
定义
首先给出定义:
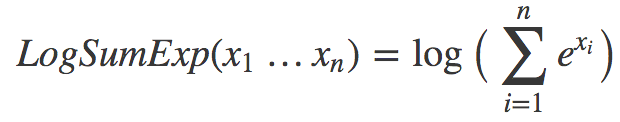
我们什么时候会见到这样的式子?常见的一个地方是计算softmax函数的交叉熵损失。softmax函数可以见下式所示:
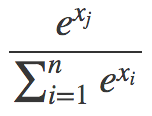
你可以把softmax函数看成一种接受任何数字并转换为概率分布的非线性方法。至于交叉熵,只需了解它是对softmax函数取对数。这就涌现出了LogSumExp模式:
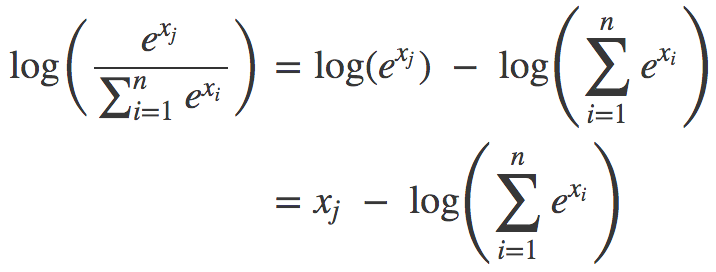
数值稳定性
首先,从纯数学的角度来说,LogSumExp没什么特别的。但是,当我们讨论计算机上的数学时,LogSumExp就特别起来了。原因在于计算机表示数字的方式。计算机使用固定数目的位元表示数字。几乎所有时刻这都没什么问题,但是,因为不可能用固定数目的位元精确表示数字的无限集合,所以有时这会导致误差。
例如,假设\(x_{i},i=1,2,3\),分别来自两个样本:{1000, 1000, 1000}和{-1000, -1000, -1000}。将这两个序列传入softmax函数会得到同一概率分布{1/3, 1/3, 1/3},然后1/3的对数是一个合理的负数。现在让我们尝试用Python算下求和中的一项:
>>> import math
>>> math.e**1000
Traceback (most recent call last):
File "", line 1, in
OverflowError: (34, 'Result too large')
再试试-1000,
>>> math.e**-1000
0.0
也不对劲。所以我们碰到了某种数值稳定性问题,即使看起来合理的输入值也会导致溢出。
解决方案
迂回方案,幸运的是,人们找到了一个很好的缓解方法,根据幂的乘法法则:
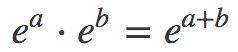
以及对数的和差公式:
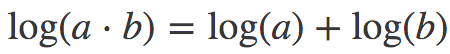
我们有:
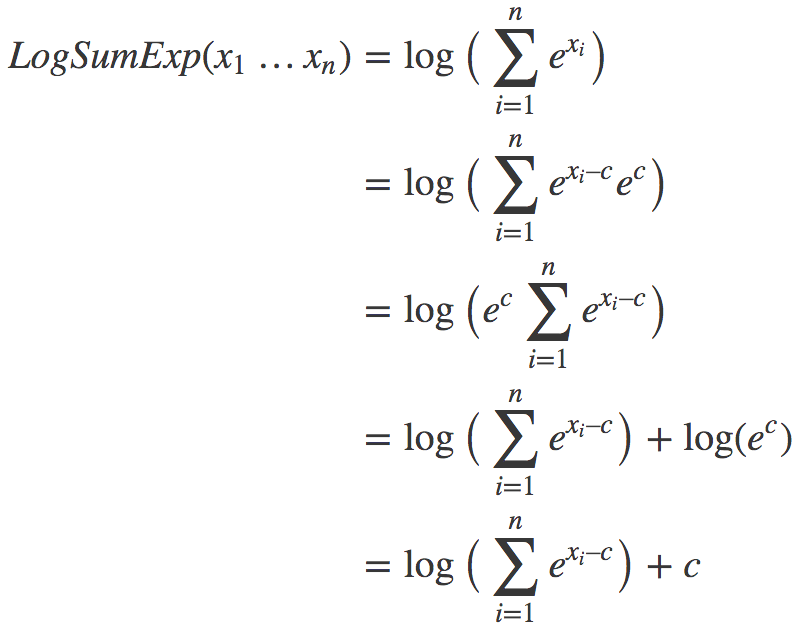
上述变换的关键在于,我们引入了一个不牵涉log或exp函数的常数项\(c\)。现在我们只需为\(c\)选择一个在所有情形下有效的良好的值。结果发现,\(max(x_1,...,x_n)\)很不错。
由此我们可以构建对数softmax的新表达式:
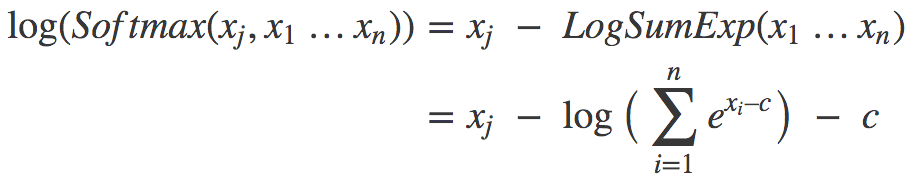
现在我们用这个新表达式计算之前的两个样本。
对{1000, 1000, 1000}而言,c = 1000,所以\(x_i-c\)恒为零,代入上式,我们有:
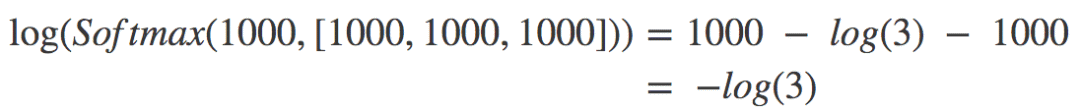
\(log(3)\)是一个很合理的数字,计算机计算起来毫无问题。所以上面的样本没问题。同理,{-1000, -1000, -1000}也没问题。
结论
如果\(x_i\)的值都不会造成稳定性问题,那么“朴素”版本的LogSumExp可以很好地工作。但“改良”版同样可以工作。如果至少有一个\(x_i\)的值很大,那么朴素版本会溢出,改良版不会。其他类似的大数值\(x_i\)同理,而并不大的那些\(x_i\),基本上逼近零。对于绝对值较大的负数,翻转下符号,道理是一样的。
所以,尽管并不完美,我们在大多数情况下能够得到相当合理的表现,而不会溢出。


