pytorch中的梯度累加(Gradient Accumulation)

PyTorch中，在反向传播前为什么要手动将梯度清零？

原因在于，在PyTorch中，计算得到的梯度值会进行累加,而这样的好处，可以从内存消耗的角度来看。
在PyTorch中，multi-task任务一个标准的train from scratch流程为:

for idx, data in enumerate(train_loader):
    xs, ys = data
    pred1 = model1(xs)
    pred2 = model2(xs)
    

    loss1 = loss_fn1(pred1, ys)
    loss2 = loss_fn2(pred2, ys)
    
    ******
    loss = loss1 + loss2
    optmizer.zero_grad()
    loss.backward()
    ++++++
    optmizer.step()

从PyTorch的设计原理上来说，在每次进行前向计算得到pred时，会产生一个用于梯度回传的计算图，这张图储存了进行back propagation需要的中间结果，当调用了.backward()后，会从内存中，将这张图进行释放。上述代码执行到******时，内存中是包含了两张计算图的，而随着求和得到loss，这两张图进行了合并，而且大小的变化可以忽略。执行到++++++时，得到对应的grad值并且释放内存。这样，训练时必须存储两张计算图，而如果loss的来源组成更加复杂，内存消耗会更大。

为了减小每次的内存消耗，借助梯度累加，又有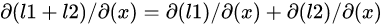image,有如下变种:

for idx, data in enumerate(train_loader):
    xs, ys = data
    
    optmizer.zero_grad()
    # 计算d(l1)/d(x)
    pred1 = model1(xs) #生成graph1
    loss1 = loss_fn1(pred1, ys)
    loss1.backward()  #释放graph1

    # 计算d(l2)/d(x)
    pred2 = model2(xs)#生成graph2
    loss2 = loss_fn2(pred2, ys)
    loss2.backward()  #释放graph2

    # 使用d(l1)/d(x)+d(l2)/d(x)进行优化
    optmizer.step()

借助梯度累加，避免同时计算多个损失时,存储多个计算图。可以从代码中看出，利用梯度累加，可以在最多保存一张计算图的情况下，进行multi-task任务的训练。另外一个理由就是，在内存大小不够的情况下，叠加多个batch的grad，作为一个大batch进行迭代，因为二者得到的梯度是等价的综上可知，这种梯度累加的思路是对内存的极大友好，是由FAIR的设计理念出发的。

梯度累加(Gradient Accumulation)

我们在训练神经网络的时候，超参数batch size的大小会对最终的模型效果产生很大的影响。一定条件下，batch size设置的越大，模型就会越稳定。batch size的值通常设置在 8-32 之间，但是当我们做一些计算量需求大的任务(例如语义分割、GAN等)或者输入图片尺寸太大的时候，我们的batch size往往只能设置为2或者4，否则就会出现 “CUDA OUT OF MEMORY” 的不可抗力报错。贫穷是促进人类进步的阶梯，如何在有限的计算资源的条件下，训练时采用更大的batch size呢？这就是梯度累加(Gradient Accumulation)技术了。
我们以Pytorch为例，一个神经网络的训练过程通常如下：

for i, (inputs, labels) in enumerate(trainloader):
    optimizer.zero_grad()                   # 梯度清零
    outputs = net(inputs)                   # 正向传播
    loss = criterion(outputs, labels)       # 计算损失
    loss.backward()                         # 反向传播，计算梯度
    optimizer.step()                        # 更新参数
    if (i+1) % evaluation_steps == 0:
        evaluate_model()

从代码中可以很清楚地看到神经网络是如何做到训练的：

  1. 将前一个batch计算之后的网络梯度清零
  2. 正向传播，将数据传入网络，得到预测结果
  3. 根据预测结果与label，计算损失值
  4. 利用损失进行反向传播，计算参数梯度
  5. 利用计算的参数梯度更新网络参数

下面来看梯度累加是如何做的：

for i, (inputs, labels) in enumerate(trainloader):
    outputs = net(inputs)                   # 正向传播
    loss = criterion(outputs, labels)       # 计算损失函数
    loss = loss / accumulation_steps        # 损失标准化
    loss.backward()                         # 反向传播，计算梯度
    if (i+1) % accumulation_steps == 0:
        optimizer.step()                    # 更新参数
        optimizer.zero_grad()               # 梯度清零
        if (i+1) % evaluation_steps == 0:
            evaluate_model()
  1. 正向传播，将数据传入网络，得到预测结果
  2. 根据预测结果与label，计算损失值
  3. 利用损失进行反向传播，计算参数梯度
  4. 重复1-3，不清空梯度，而是将梯度累加
  5. 梯度累加达到固定次数之后，更新参数，然后将梯度清零

总结来讲，梯度累加就是每计算一个batch的梯度，不进行清零，而是做梯度的累加，当累加到一定的次数之后，再更新网络参数，然后将梯度清零。通过这种参数延迟更新的手段，可以实现与采用大batch size相近的效果。在平时的实验过程中，我一般会采用梯度累加技术，大多数情况下，采用梯度累加训练的模型效果，要比采用小batch size训练的模型效果要好很多。
一定条件下，batch size越大,训练效果越好，梯度累加则实现了batch size的变相扩大，如果 accumulation_steps 为8，则batch size '变相' 扩大了8倍，是解决显存受限的一个不错的trick，使用时需要注意，学习率也要适当放大。
参考：
PyTorch中在反向传播前为什么要手动将梯度清零？
PyTorch中的梯度累加
梯度累加(Gradient Accumulation)

posted on 2021-07-25 12:37  朴素贝叶斯  阅读(2366)  评论(1)  编辑  收藏  举报

导航