CoNi-MPC: Cooperative Non-inertial Frame Based Model Predictive Control
CoNi-MPC: Cooperative Non-inertial Frame Based Model Predictive Control
摘要
- 提出了多机器人协同的系统,可用于在移动的平台上降落、和目标物保持特定的相对运动等任务
- 直接在目标的坐标系中控制UAV,不对目标的运动做假设
- 在非惯性系(non-inertial frame)中使用NMPC
- 需要目标的相对姿态和速度、角速度以及加速度
- 该框架不需要准确的状态估计、对目标运动模型的先验知识、频繁的重规划
引言
- 目标的相对姿态和速度可由相对定位方法获得
- 目标的角速度和加速度可由MEMS IMU传感器获得
主要贡献:
- 提出了在非惯性系中使用MPC的无人机-目标(drone-target)相对运动框架。不需要目标在世界坐标系中的姿态和运动。
- 通过相对运动模型,将和目标相关的元素组合在一起并使用目标坐标系中的IMU信息替换。避免了使用世界坐标系中的数据。
- MPC控制器作为一个统一的框架支持多种无人机-目标交互的任务。无需频繁的重规划。
![image-20240206000045533]()
相关工作
其他工作需要全局状态估计和频繁的全局路径重规划,本文的方法可避免这两项
问题表述和CoNi-MPC
符号
![Untitled]()
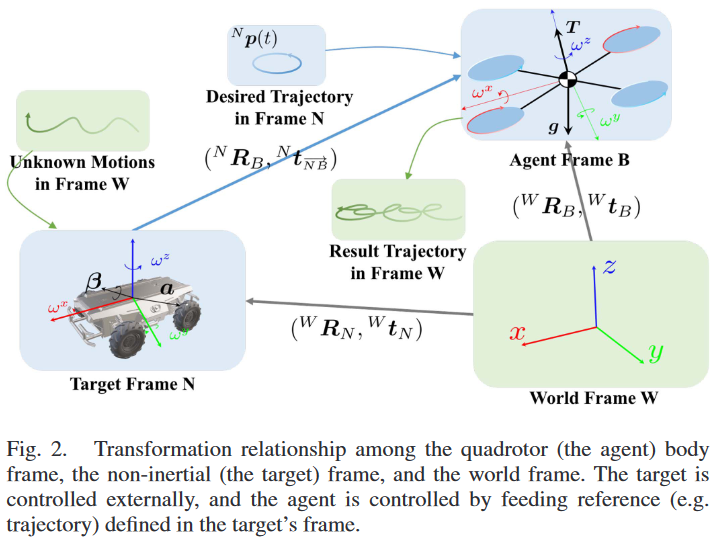
\(B\):智能体的自身坐标系;\(N\):目标的自身坐标系;\(W\):世界惯性坐标系
左侧上标:以该坐标系为参考;右侧下标:该坐标系的物理量
标量:小写字母;向量:加粗小写字母;矩阵:加粗大写字母
\(\odot\):四元数的Hamilton乘积;\([\boldsymbol{t}]_{\times}\):向量\(\boldsymbol{t}\)的反对称矩阵(skew-symmetric matrix)
四元数的Hamilton乘积,也称为四元数的乘法,是定义在四元数集合上的一种二元运算。
向量的反对称矩阵通常用于表示三维向量的叉积。给定一个三维向量\(\mathbf{v} = (v_1, v_2, v_3)\),其对应的反对称矩阵\(A\)定义如下:
\(A = \begin{pmatrix}
0 & -v_3 & v_2 \\
v_3 & 0 & -v_1 \\
-v_2 & v_1 & 0
\end{pmatrix}\)
两个向量\(\mathbf{u}\)和\(\mathbf{v}\)的叉积可以表示为\(\mathbf{u} \times \mathbf{v} = A\mathbf{u}\),其中\(A\)是向量\(\mathbf{v}\)的反对称矩阵。
非惯性系中的四旋翼系统模型
![Untitled]()
相对位置为
\[{ }^N \boldsymbol{p}_B={ }^N \boldsymbol{R}_W \boldsymbol{t}_{\overrightarrow{N B}}
\]
其中\(\boldsymbol{t}_{\overrightarrow{N B}}=\boldsymbol{t}_B-\boldsymbol{t}_N\)是由坐标系\(N\)指向坐标系\(B\)的平移向量(translational vector)
相对速度为
\[\begin{aligned}{ }^N \dot{\boldsymbol{p}}_B={ }^N \boldsymbol{v}_B & =\frac{d}{d t}\left({ }^N \boldsymbol{R}_W\right) \boldsymbol{t}_{\overrightarrow{N B}}+{ }^N \boldsymbol{R}_W \dot{\boldsymbol{t}}_{\overrightarrow{N B}} \\& =-\left[{ }^N \boldsymbol{\Omega}_N\right]_{\times}{ }^N \boldsymbol{R}_W \boldsymbol{t}_{\overrightarrow{N B}}+{ }^N \boldsymbol{R}_W \dot{\boldsymbol{t}}_{\overrightarrow{N B}} \\& =-\left[{ }^N \boldsymbol{\Omega}_N\right]{ }^N \boldsymbol{p}_B+{ }^N \boldsymbol{R}_W \dot{\boldsymbol{t}}_{\overrightarrow{N B}}\end{aligned}
\]
相对加速度为
\[\begin{aligned}{ }^N \dot{\boldsymbol{v}}_B= & -\frac{d}{d t}\left(\left[{ }^N \boldsymbol{\Omega}_N\right]_{\times}\right)^N \boldsymbol{p}_B-\left[{ }^N \boldsymbol{\Omega}_N\right]_{\times}{ }^N \dot{\boldsymbol{p}}_B \\& -\left[{ }^N \boldsymbol{\Omega}_N\right]_{\times}{ }^N \boldsymbol{R}_W \dot{\boldsymbol{t}}_{\overrightarrow{N B}}+{ }^N \boldsymbol{R}_W \ddot{\boldsymbol{t}}_{\overrightarrow{\mathrm{NB}}} \\= & -\frac{d}{d t}\left(\left[{ }^N \boldsymbol{\Omega}_N\right]_{\times}\right)^N \boldsymbol{p}_B-\left[{ }^N \boldsymbol{\Omega}_N\right]_{\times}{ }^N \boldsymbol{v}_B \\& -\left[{ }^N \boldsymbol{\Omega}_N\right]_{\times}\left({ }^N \boldsymbol{v}_B+\left[{ }^N \boldsymbol{\Omega}_N\right]_{\times}{ }^N \boldsymbol{p}_B\right)+{ }^N \boldsymbol{R}_W\left(\ddot{\boldsymbol{t}}_B-\ddot{\boldsymbol{t}}_N\right) \\= & -\left[{ }^N \boldsymbol{\beta}_N\right]_{\times}{ }^N \boldsymbol{p}_B-2\left[{ }^N \boldsymbol{\Omega}_N\right]_{\times}{ }^N \boldsymbol{v}_B-\left[{ }^N \boldsymbol{\Omega}_N\right]_{\times}^2 { }^N \boldsymbol{p}_B \\& +{ }^N \boldsymbol{R}_B{ }^B \boldsymbol{T}_B+\underbrace{{ }^N \boldsymbol{R}_W \boldsymbol{g}-{ }^N \boldsymbol{R}_W \boldsymbol{a}_N}_{\text {values relying on estimations in } W}\end{aligned}
\]
其中\(\ddot{t}_B\)是四旋翼无人机的加速度,其在世界坐标系中的表达式为
\[\ddot{\boldsymbol{t}}_B={ }^W \boldsymbol{R}_B{ }^B \boldsymbol{T}_B+\boldsymbol{g}
\]
\({ }^B \boldsymbol{T}_B=[0,0, T]^{\top}\)为四个电机的归一化合推力;
\(T=\sum_i T_i, i \in\{1,2,3,4\}\)为四个电机的归一化推力;
\(\boldsymbol{g}=[0,0,-g]^{\top}\)为重力;
由\(B\)到\(N\)的旋转矩阵为
\[{ }^N \boldsymbol{R}_B={ }^N \boldsymbol{R}_W{ }^W \boldsymbol{R}_B
\]
则其对时间的导数为
\[⁍
\]
下一节会用到的四元数为
\[\begin{aligned}{ }^N \dot{\boldsymbol{q}}_B & ={ }^N \dot{\boldsymbol{q}}_W \odot{ }^W \boldsymbol{q}_B+{ }^N \boldsymbol{q}_W \odot{ }^W \dot{\boldsymbol{q}}_B \\& =-\frac{1}{2}{ }^N \boldsymbol{\Omega}_N \odot{ }^N \boldsymbol{q}_B+\frac{1}{2}{ }^N \boldsymbol{q}_B \odot{ }^B \boldsymbol{\Omega}_B\end{aligned}
\]
此时只有\(\left({ }^N \boldsymbol{R}_W \boldsymbol{g}-{ }^N \boldsymbol{R}_W \boldsymbol{a}_N\right)\)一项依赖世界坐标系,这一项表示目标在目标坐标系中的合加速度,包含投影到目标坐标系下的重力加速度\({ }^N \boldsymbol{R}_W \boldsymbol{g}\)和非惯性系自身的加速度\({ }^N \boldsymbol{a}_N\left(={ }^N \boldsymbol{R}_W \boldsymbol{a}_N\right)\),可利用非惯性系下的IMU数据进行处理。
MEMS IMU传感器的真实加速度可利用目标坐标系下的负重力计算得到,为
\[{ }^N \boldsymbol{a}_N={ }^N \boldsymbol{R}_W\left[\begin{array}{c}0 \\0 \\-g\end{array}\right]+{ }^N\left[\begin{array}{l}\hat{a}^x \\\hat{a}^y \\\hat{a}^z\end{array}\right]
\]
其中\(\hat{a}^x, \hat{a}^y, \hat{a}^z\)为IMU测得的加速度。则相对加速度可重写为
\[\begin{aligned}{ }^N \dot{\boldsymbol{v}}_B= & -\left[{ }^N \boldsymbol{\beta}_N\right]_{\times}{ }^N \boldsymbol{p}_B-2\left[{ }^N \widehat{\boldsymbol{\Omega}}_N\right]_{\times}{ }^N \boldsymbol{v}_B-\left[{ }^N \widehat{\boldsymbol{\Omega}}_N\right]_{\times}^2{ }^N \boldsymbol{p}_B \\& +{ }^N \boldsymbol{R}_B{ }^B \boldsymbol{T}_B-{ }^N \widehat{\boldsymbol{a}}_N\end{aligned}
\]
其中\({ }^N \widehat{\boldsymbol{a}}_N ,{ }^N \widehat{\boldsymbol{\Omega}}_N\)分别为IMU测得的线加速度和角速度。
CoNi-MPC
CoNi-MPC:Cooperative Non-inertial Frame Based Model Predictive Control
系统的状态为\(\boldsymbol{x}=\left[{ }^N \boldsymbol{p}_B ;{ }^N \boldsymbol{v}_B ;{ }^N \boldsymbol{q}_B ;{ }^N \widehat{\boldsymbol{a}}_N ;{ }^N \widehat{\boldsymbol{\Omega}}_N ;{ }^N \boldsymbol{\beta}_N\right] \in \mathbb{R}^{19}\)
角速度的导数满足\(\frac{d}{d t}\left({ }^N \widehat{\boldsymbol{\Omega}}_N\right)={ }^N \boldsymbol{\beta}_N\)
假设线加速度和角加速度的变化率为0,即\(**{ }^N \dot{\hat{\boldsymbol{a}}}_N=0 ,\dot{\boldsymbol{\beta}}_N=0**\)(由于它们为高阶变量,该假设对系统性能不会有很大影响)
系统的输入为\(\boldsymbol{u}=\left[T ;{ }^B \Omega_B^x ;{ }^B \Omega_B^y ;{ }^B \Omega_B^z\right] \in \mathbb{R}^4\)
定义二次函数形式的成本为
\[\boldsymbol{C}(\boldsymbol{x}, \boldsymbol{u})=\left\|\boldsymbol{x}(t)-\boldsymbol{x}(t)_{r e f}\right\|_{\boldsymbol{Q}}+\left\|\boldsymbol{u}(t)-\boldsymbol{u}_h\right\|_{\boldsymbol{R}}
\]
其中\(\|\boldsymbol{x}\|_{\boldsymbol{M}}=\boldsymbol{x}^{\top} \boldsymbol{M} \boldsymbol{x}\)且\(\boldsymbol{u}_h=[g ; 0 ; 0 ; 0]\)为悬停输入(hover input)
最终的离散优化问题为
\[\begin{aligned}
\min _{\boldsymbol{u}_0, \ldots, \boldsymbol{u}_{N-1}} & \sum_{k=0}^{N-1}\left(\left\|\boldsymbol{x}(k)-\boldsymbol{x}(k)_{{ref }}\right\|_{\boldsymbol{Q}}+\left\|\boldsymbol{u}(k)-\boldsymbol{u}_h\right\|_{\boldsymbol{R}}\right) \\
& +\left\|\boldsymbol{x}(N)-\boldsymbol{x}(N)_{{ref }}\right\|_{\boldsymbol{Q}_{{final }}} \\
\text { s.t. } & \boldsymbol{x}(0)=\boldsymbol{x}_0 \\
& \boldsymbol{x}(k+1)=f_d(\boldsymbol{x}(k), \boldsymbol{u}(k)) \\
& T_{\min } \leq T \leq T_{\max } \\
& \left\|^B \Omega_B^x\right\| \leq \Omega_{\mathrm{rp}} \\
& \left\|^B \Omega_B^y\right\| \leq \Omega_{\mathrm{rp}} \\
& \left\|^B \Omega_B^z\right\| \leq \Omega_{\mathrm{yaw}}
\end{aligned}
\]
文中把参考轨迹分为两类:
- 固定点方案(Fixed Point Scheme,Leader and Follower)
- 固定计划方案(Fixed Plan Scheme,Complex Trajectories)
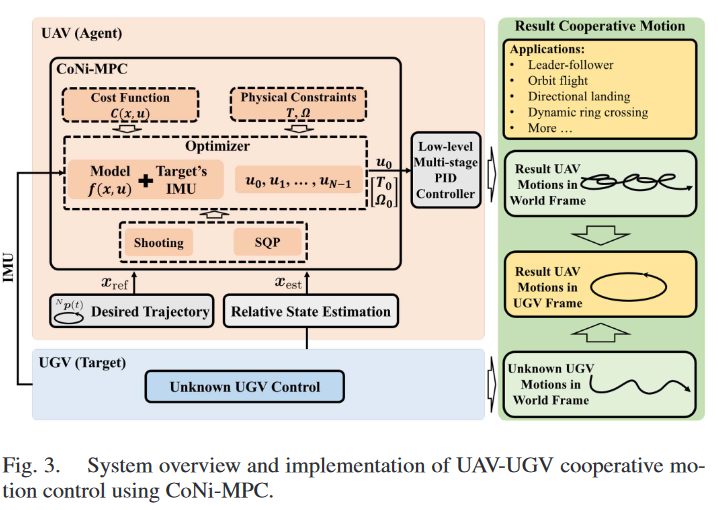
部署
![Untitled]()
- 上层控制器:使用ACADO工具包部署CoNi-MPC控制器,生成控制指令\(\boldsymbol{u}_0\)
- 下层控制器:多级PID
- CoNi-MPC通过多次打靶技术(multiple shooting technique)和Runge-Kutta积分求解优化问题
- 对非惯性系下的IMU数据进行平均信号滤波(average signal filter)
- 时间窗口为2s,离散时间步长为0.1s,MPC实际的控制回路实际约10ms
- \({ }^N \widehat{\boldsymbol{a}}_N,{ }^N \widehat{\boldsymbol{\Omega}}_N,{ }^N \boldsymbol{\beta}_N\)的惩罚项设置为\(\boldsymbol{Q}(i, i)=0, \forall i=10 \ldots 19\)
- 在仿真和实验中,角加速度很难获取,故在参数估计(estimation)和参考值(reference)中都设置为0
实验
把包含xy平面距离、线速度和角速度的\((r, v, \omega)\)纳入系统模型:
\[\begin{aligned}{ }^N \boldsymbol{v}_B^x & =\left({ }^N \boldsymbol{R}_W \dot{\boldsymbol{t}}_B\right)^x-v \\{ }^N \boldsymbol{v}_B^y & =\left({ }^N \boldsymbol{R}_W \dot{\boldsymbol{t}}_B\right)^y-w r \\{ }^N \boldsymbol{v}_B^z & =\left({ }^N \boldsymbol{R}_W \dot{\boldsymbol{t}}_B\right)^z \\{ }^N \dot{\boldsymbol{v}}_B^x & =2 \omega\left({ }^N \boldsymbol{R}_W \dot{\boldsymbol{t}}_B\right)^y+\left({ }^N \boldsymbol{R}_B{ }^B \boldsymbol{T}_B\right)^x-\left({ }^N \widehat{\boldsymbol{a}}_N\right)^x \\{ }^N \dot{\boldsymbol{v}}_B^y & =-2 \omega\left({ }^N \boldsymbol{R}_W \dot{\boldsymbol{t}}_B\right)^x+2 \omega v+\left({ }^N \boldsymbol{R}_B{ }^B \boldsymbol{T}_B\right)^y-\left({ }^N \widehat{\boldsymbol{a}}_N\right)^y \\{ }^N \dot{\boldsymbol{v}}_B^z & =\left({ }^N \boldsymbol{R}_B{ }^B \boldsymbol{T}_B\right)^z-9.8\end{aligned}
\]
其余没细看o( ̄︶ ̄)o
结论
- 提出了四旋翼无人机在非惯性系中具有线运动和角运动的动力学模型
- CoNi-MPC避免在世界坐标系下的全局状态估计
- 避免依赖先验知识,不需要进行复杂的轨迹重规划
- 相对状态(姿态和速度)、角速度和加速度可分别由相对定位方法和MEMS IMU传感器获得





 浙公网安备 33010602011771号
浙公网安备 33010602011771号