参数曲线(贝塞尔曲线、B样条曲线和NURBS曲线)
参数曲线
相关概念
齐次坐标:齐次坐标到笛卡尔坐标的变换
有理曲线:齐次形式的参数曲线称为有理曲线
连续性
几何连续性
-
以弧长为参数时,
-
存在两个参数化方式,使得
注意:
贝赛尔曲线
构建贝赛尔曲线
给定空间中
其中系数定义如下
-
贝塞尔曲线可视为对所有控制点的加权平均
-
线段
-
贝塞尔曲线具有以下性质:
-
-
贝塞尔曲线经过
-
非负性:所有基函数均非负
-
单位分解(partition of unity):所有基函数之和为1
-
凸包性质:贝塞尔曲线完全位于给定控制点的凸包内
-
变分递减性质(variation diminishing property):没有一条直线与贝塞尔曲线相交的次数多于与曲线控制折线相交的次数
-
仿射不变性(affine invariance):对贝塞尔曲线的仿射变换等价于对控制点的仿射变换
如果
移动控制点
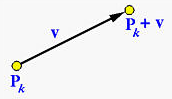
原控制点
更改单个控制点,贝塞尔曲线上所有的点都将移动到新位置,曲线形状会发生整体的变化
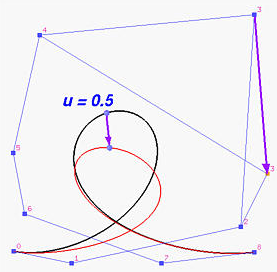
德卡斯特里奥算法(de Casteljau's algorithm)
直接法(直接把
几何解释
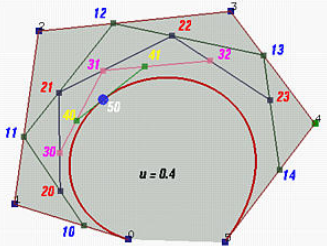
定义第
-
先对点
-
对点
-
该操作重复
实际计算
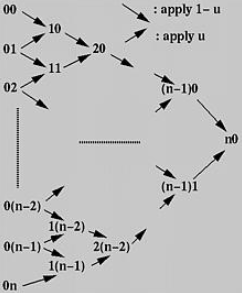
计算步骤如下:
-
把所有控制点
-
新点为左边两个点的加权和,左上方的点权重为
-
按此规则迭代至得到

递归关系
直接按递归关系计算的函数为

上述函数会有大量的重复计算,如下图中的
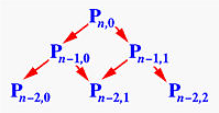
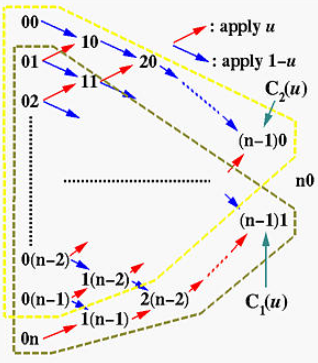
特殊性质
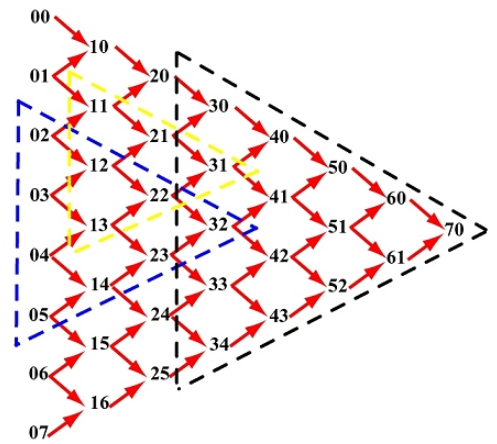
如果把某一列中一组连续的点作为贝塞尔曲线的控制点,那利用de Casteljau算法计算时,曲线上的点就是等边三角形内所选点形成的边的对面的顶点,如下图所示
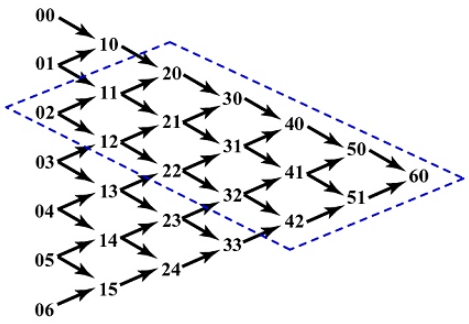
算法的正确性
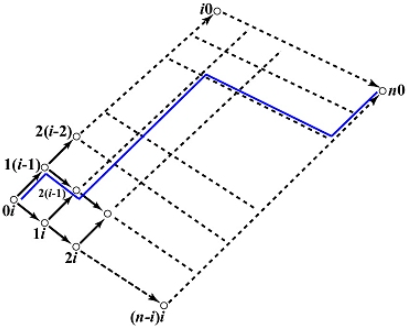
-
每个控制点对
-
控制点经过平行四边形中的每条路径都对
-
考虑到一条路径传播的贡献只和起点与终点的相对位置有关,和路径形状无关,由
-
平行四边形内路径的总数恰好为组合数
-
易得,所有路径的贡献总和满足贝塞尔曲线关系式
贝塞尔曲线的导数
由于控制点是与
定义
连接贝塞尔曲线
- 满足

- 满足
导数与de Casteljau算法的关系
贝塞尔曲线的导数可写为
定义
则贝塞尔曲线的导数可表示为
因此,理论上,可以使用de Casteljau算法来计算
高阶导数
定义
则贝塞尔曲线的
利用de Casteljau算法计算特定
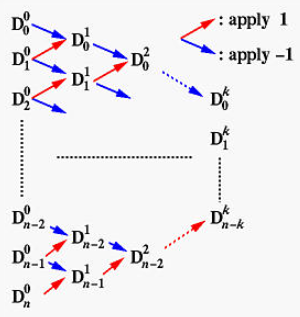
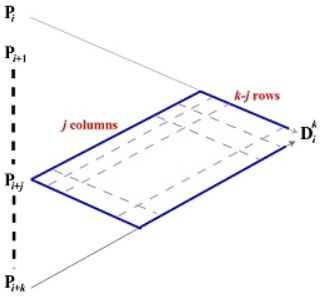
- 把de Casteljau算法应用在第
贝塞尔曲线的分段
贝塞尔曲线的分段需要满足以下条件:
-
将给定的贝塞尔曲线
-
新生成的贝塞尔曲线必须和原贝塞尔曲线同阶
贝塞尔曲线分段的新控制点可借助de Casteljau算法得到,以6阶贝塞尔曲线为例:
-
左侧折线由点
-
右侧折线由点
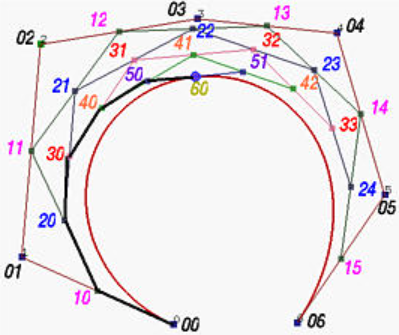
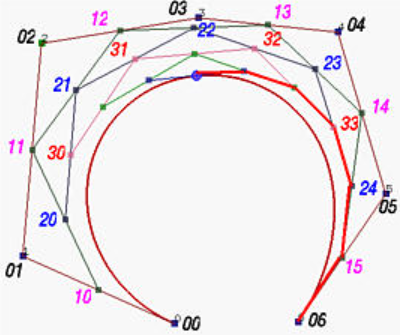
- 以上两组控制点也对应如下de Casteljau算法中红圈内顺箭头方向的一组点和蓝圈内逆箭头方向的一组点
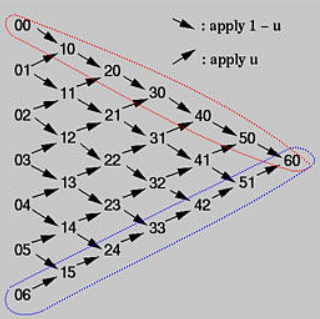
算法的正确性
以原贝塞尔曲线
- 设原曲线为
- 由de Casteljau算法的特殊性质可得,
- 将由
- 考虑点
- 由于
贝塞尔曲线的阶数提升(degree elevation)
阶数的提升要求不改变原贝塞尔曲线的形状,步骤如下
-
假设
-
由于升阶的曲线也经过
-
新控制点记为
阶数提升算法类似de Casteljau算法,但比例不是常数
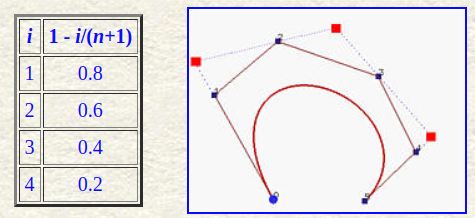
随着阶数提升,控制折线逐渐收敛至贝塞尔曲线
算法的正确性
整体推导思路类似数学归纳法,利用两条曲线的任意阶导数处处相等的性质,通过使
该推导只说明了必要性,推导过程见网页
B样条(B-spline)曲线
B样条基函数
定义
不同于贝塞尔基函数,B样条基函数具有以下特点:
-
定义域(domain)由节点划分
-
只在几个相邻的子区间非零,而非在整个区间内都非零
首先引入如下定义:
| 概念 | 定义 |
|---|---|
| 节点(knots) | 非递减序列 |
| 节点向量(knot vector) | |
| 第 |
半开半闭区间 |
| 均匀(uniform)节点向量/节点序列 | 所有节点区间的跨度都相等 |
| 非均匀(non-uniform) 节点向量/节点序列 | 存在节点区间的跨度不相等 |
| 单节点(simple knot) | 只出现1次的节点 |
| 重数(multiplicity)为 |
出现 |
第
该递归公式可通过三角形的方案计算
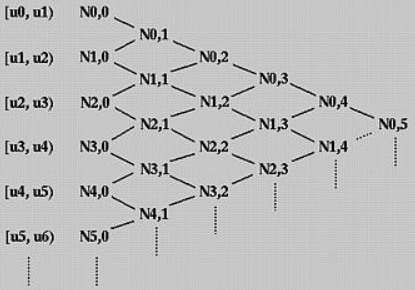
特殊性质
-
基函数
-
任意节点区间
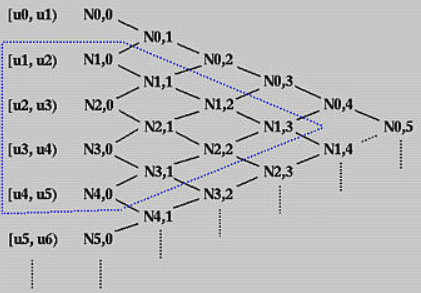
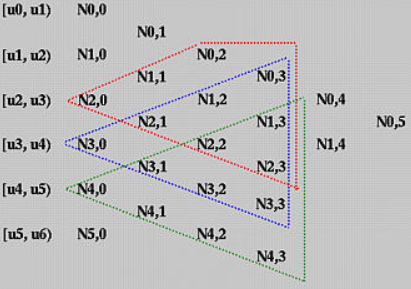
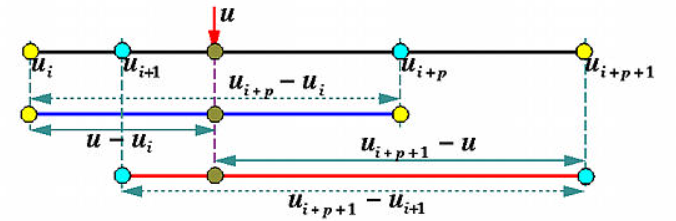
重要性质
-
-
非负性:
-
局部支撑(local support):
-
任意节点区间
-
单位分解(partition of unity):区间
-
节点数为
-
基函数
-
多重节点的影响
-
每个
-
在
-
单节点
-
将
-
将
-
B样条曲线
定义
给定
其中节点
B样条曲线可分为如下3类:开放(open)B样条曲线,固定(clamped)B样条曲线,闭合(closed)B样条曲线
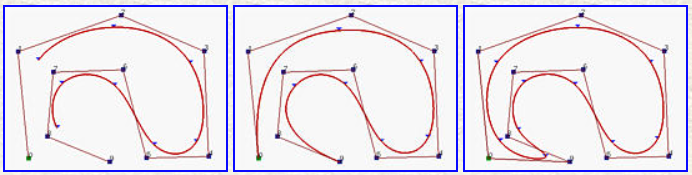
固定曲线
固定曲线的前
除首尾节点外其余节点分布均匀,故也称准均匀B样条曲线
开放曲线
如果首末节点的重数小于
“完全支撑”(full support):节点区间
在节点区间
考虑
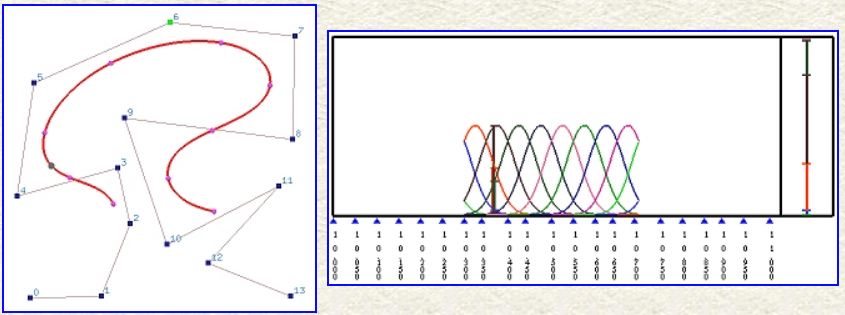
闭合曲线
构造由
-
包裹控制点(wrapping control points)
-
构造步骤:
-
设计均匀节点序列
-
让首尾
-
-
曲线在
-
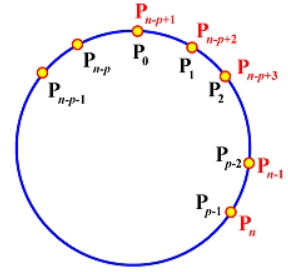
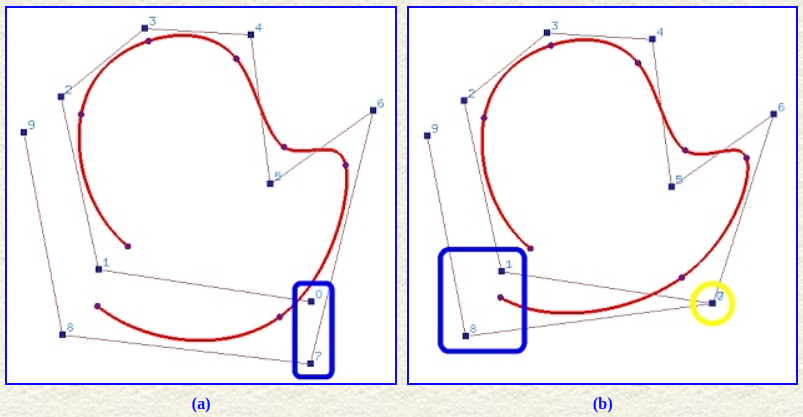
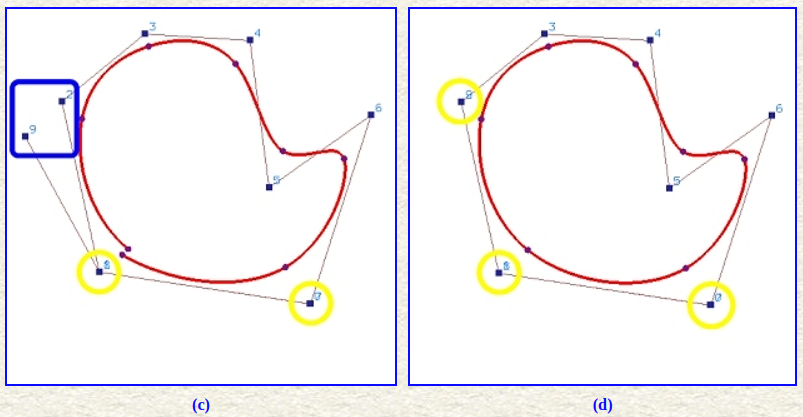
-
包裹节点(wrapping knots)
-
网页中内容有误,思路可能是利用给定控制点,和与原节点向量部分相同的新节点向量,新构造一段B样条曲线使得原开放曲线闭合
-
构造步骤:-
添加新的控制点,由于首尾控制点重合,此时控制点个数可认为仍是 -
找到合适的节点序列,该节点序列的优势在于不必为均匀的 -
添加和前个节点相等的个节点,即,以引导受影响的曲线末端和受影响的曲线开端重合,此时节点数量为 -
由上述个控制点和个节点定义的次开放曲线即为闭合曲线
-
-
曲线在处满足连续 -
曲线定义域为
-
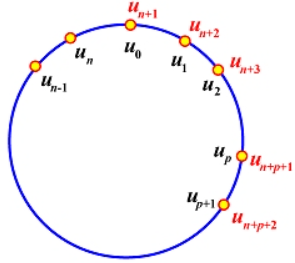
重要性质
-
B样条曲线是分段曲线,每一段都是
- 一般来说,次数越低,B样条曲线越接近其控制折线(以下三图的次数分别为7、5、3)
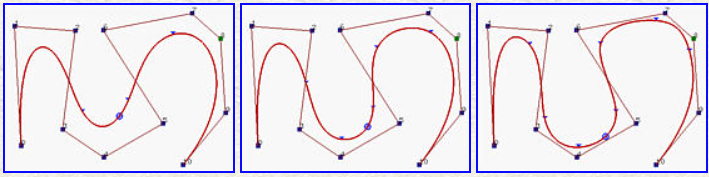
-
必满足
-
固定B样条曲线经过
- 由于
- 由于
-
强凸包性质:如果
- 在
- 在
-
局部修改性质(local modification scheme):改变控制点
-
-
变分递减性质:如果曲线位于平面(或空间)中,则直线(或平面)与B样条曲线相交的次数不超过与曲线的控制折线相交的次数
-
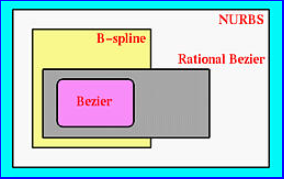
贝塞尔曲线是B样条曲线的特例:当
-
仿射不变性:对B样条曲线的仿射变换等价于对控制点的仿射变换
优点:
-
B样条曲线可以转化为贝塞尔曲线
-
B样条曲线满足贝塞尔曲线的所有性质
-
B样条曲线控制更灵活
-
曲线的次数与控制点的数量相对独立,使用较低次数的曲线仍可保持大量控制点
-
可改变控制点的位置进行局部而非全局修改
-
强凸包性质带来更精细的形状控制
-
缺点:
- 不能表示部分曲线,例如圆和椭圆,需要用到NURBS曲线
重要算法
节点插入
单次插入
节点插入:
-
在现有的节点向量中添加一个新的节点,而不改变曲线的形状
-
新节点可以和原节点相等,使得其重数加1
-
控制点数量必须加1(曲线次数改变会影响全局的形状,因此须保持不变)
若新节点
-
-
需要找到
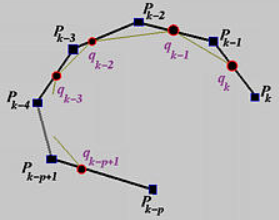
- 新控制点
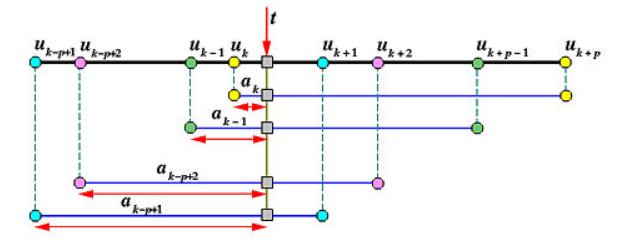
多次插入
如在
- 系数
-
插入
-
列出受影响的
-
忽略最后
-
依次计算第1到第
-
新的控制点如下图蓝色多边形内所示
-
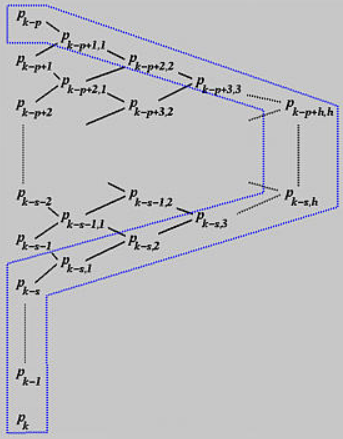
计算步骤总结如下图

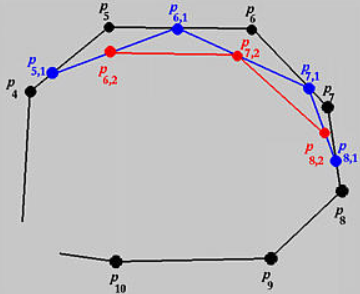
计算过程可理解为如下割角(corner cutting)的过程
德布尔算法(de Boor's algorithm)
de Boor算法用于计算在特定
-
增加节点重数会减少该节点处非零基函数的数量
-
-
考虑单位分解性质,该唯一非零基函数在该
-
如果重复插入新节点
de Boor算法的流程可总结如下

得到最后生成的新控制点
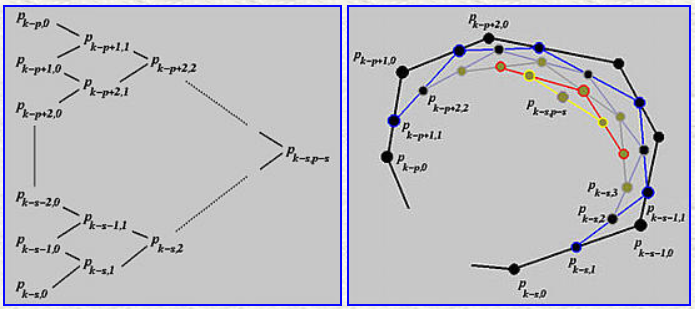
de Boor算法和de Casteljau算法的不同如下
| de Boor算法 | de Casteljau算法 | |
|---|---|---|
| 计算新控制点的系数 | 由列和控制点的序数决定 | 为定值 |
| 参与计算的控制点 | 只有 |
所有控制点 |
当节点向量中只有两个重数为
B样条曲线的分段
B样条曲线的分段使用de Boor算法,其余和贝塞尔曲线的分段完全相同
把B样条曲线分为
-
选择控制点
-
使用de Boor算法插入新节点
-
从
-
上述过程中选中的点作为
-
-
上述操作如下左图所示,选出的控制点满足下右图的三角形计算方案中蓝色多边形显示的关系
-
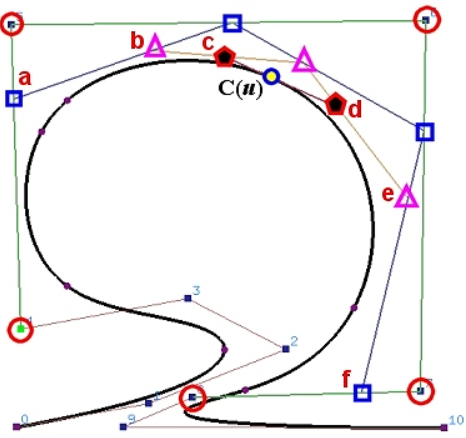
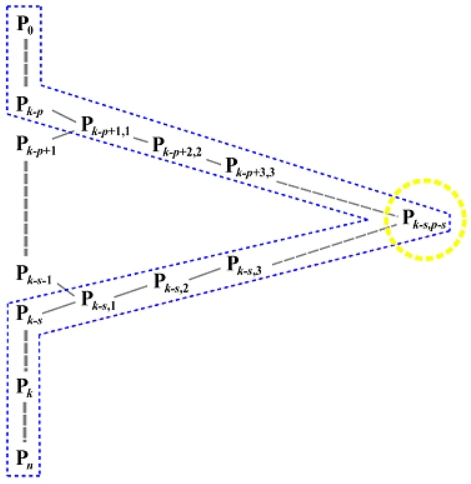
-
选择节点
-
增加
-
-
-
如果
-
会引入大量新的控制点
-
B样条曲线在
NURBS曲线
NURBS(Non-Uniform Rational B-Splines)曲线,即非均匀有理B样条曲线,是B样条曲线通过齐次坐标到有理曲线的推广,可表示圆、椭圆和许多其他不能用多项式表示的曲线
定义
给定
把控制点
将上述
把
最后得到的表达式为
NURBS曲线有如下易得的结论:
-
若所有权中均为1,则NURBS曲线退化为B样条曲线
-
NURBS曲线是有理的
-
三维空间中的NURBS曲线仅仅是四维空间中B样条曲线的射影
重要性质
给定
其中
NURBS基函数的重要性质
-
-
非负性:
-
局部支撑:假设
-
在任意节点区间
-
单位分解:节点区间
-
节点数为
-
基函数
-
-
如果
NURBS曲线的重要性质
-
NURBS曲线
-
必有
-
强凸包性质:如果
-
局部修改性质:改变控制点
-
-
变分递减性质:如果曲线位于平面(或空间)中,则直线(或平面)与B样条曲线相交的次数不超过与曲线的控制折线相交的次数
-
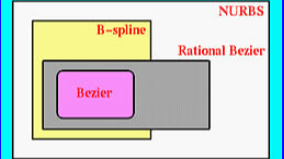
贝塞尔曲线和B样条曲线是NURBS曲线的特例
-
当所有权重相等,NURBS曲线等价于B样条曲线
-
当所有权重相等,
-
-
射影不变性(projective invariance):对NURBS曲线的射影变换等价于对控制点的射影変換
节点插入算法
节点插入的步骤如下(例子见网页):
-
把给定的三维NURBS曲线转换为四维的B样条曲线
-
对四维的B样条曲线进行节点插入
-
把新的控制点集射影回三维
有理贝塞尔曲线
把四维贝塞尔曲线射影到超平面
其中
有理贝塞尔曲线具有以下特点:
-
不具有局部修改性质
-
满足射影不变性质(仿射变换是射影变换的子集)
圆锥曲线
唯一确定圆锥曲线的五个条件:
-
由三个非共线点
-
假设圆锥曲线经过
- 如果
- 方程的梯度如下
-
目前可以得到四个方程
-
-
-
在
-
在
-
-
第五个方程则需要再找到一个在曲线上的点,改点应位于控制三角形的内部,以保持凸包性质
-
该点受控制点
- 2次有理贝塞尔曲线的表达式为
- 通过把
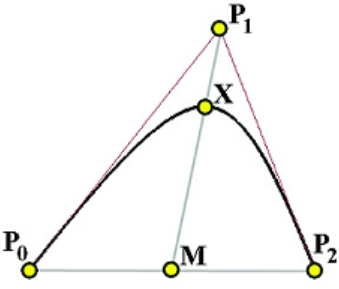
-
根据射影几何中的定理,由三个非共线控制点
-
-
-
-
圆弧和圆
圆弧使用有理贝塞尔曲线表示,整圆使用NURBS曲线表示,详情见网页
圆弧
圆是椭圆的特例,根据下图所示关系和圆锥曲线小节内容,
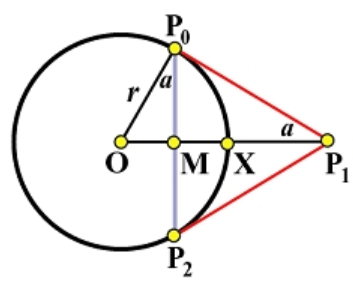
整圆
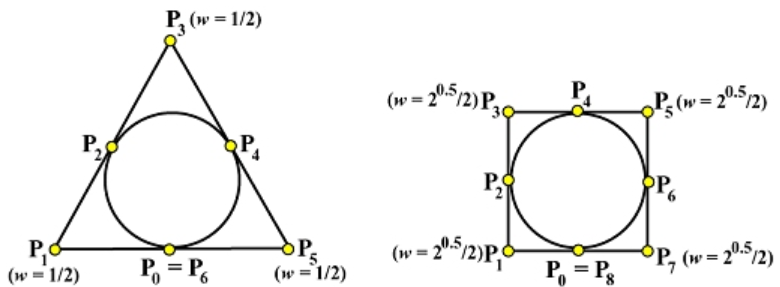
多个圆弧拼接在一起即为整圆:
-
用三角形定义整圆,则节点为
-
用正方形定义整圆,则节点为



 https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/
https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具