1.什么是卡诺图
将n变量的所有最小项用一个小方块表示,并使具有逻辑相邻的最小项在几何位置上也相邻的排列起来,所得到的图形成为n变量最小项的卡诺图。
!!!逻辑相邻性--切忌不可以按自然二进制数从小到大的顺序排列,必须按照下图进行排列,确保相邻的两个最小项仅有一个变量不同。
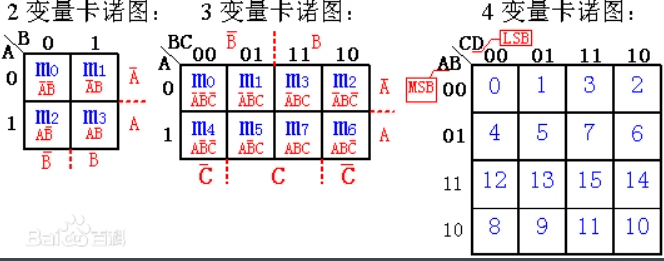
其中任何一行或者一列的两端处的最小项也仅有一个变量不同,他们也具有逻辑相邻性。
2.用拉诺图表示逻辑函数
1)把逻辑函数化为最小项之和的形式
2)在卡诺图对应最小项填1,其他位置补零
3.卡诺图化简
1)合并最小项原则
两个最小项相邻,可合并为一项并消去一对因子;
四个最小项相邻可合并为一项消去两对因子;
八个最小项相邻可合并为一项并消去三对因子。
4.具有无关项的逻辑函数及其化简
约束项:对输入变量取值所加的限制称为约束,同时将这一组变量成为具有约束的一组变量,约束项的值恒等于0。
任意项:即输入变量的值可以为0也可以为1,不影响电路的性能。在这些变量取值下,其值为1的最小项称为任意项。
这里将约束项和任意项统称为逻辑函数的无关项。在卡诺图中用“X”表示无关项,在化简逻辑函数时可以认为它是1,也可以认为它是0。
!!!化简原则:相邻最小项矩形组合最大,且矩形组合数目最少。



