虚树学习小结
虚树一开始听的时候觉得很高深,其实也是一个比较容易的东西。
可以称它是个数据结构,也可以称它是个算法,反正比较好用啦~
定义
虚树就是将原树中的点集 \(S\) 拿出来,构成一棵新的并能保持原树结构的一棵树。
保持结构,意味着对于 \(\forall x, y \in S\) ,他们的最近公共祖先 \(lca\) 也得出现在虚树中来。
举个栗子:
对于这颗树来说
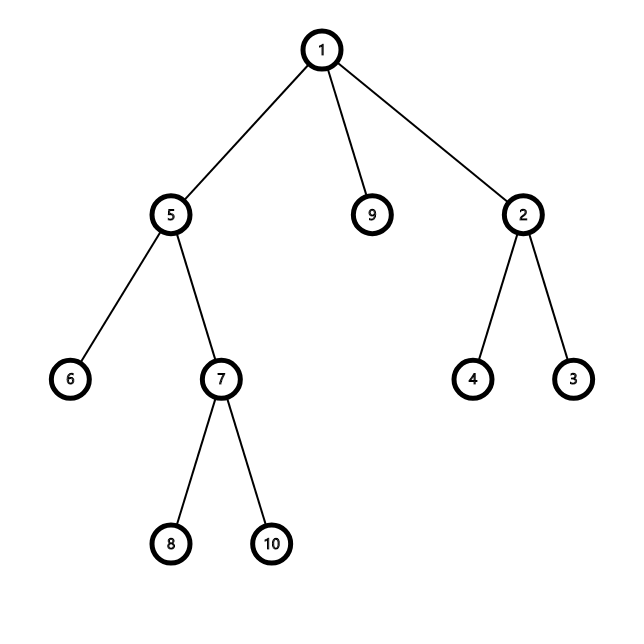
我们将 \(\{3, 6, 7\}\) 取出来变成一棵虚树就是这样的:
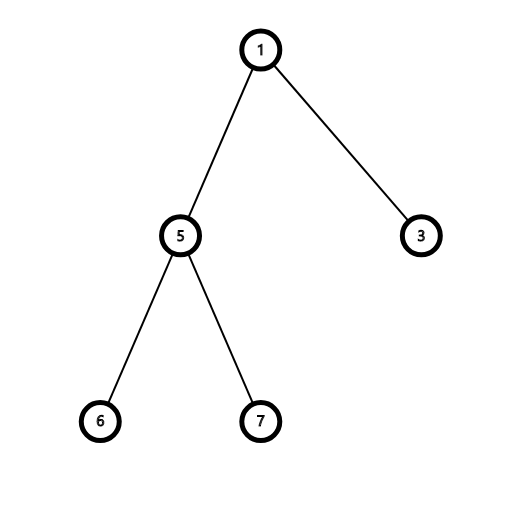
我们保留了这些点的 \(lca\) 以及它本身,然后根据他们在原树中的相对关系建了出来。
所有点对的 \(lca\) 个数是严格 \(< |S|\) 的,后面能利用构造的方式进行证明。
构建
首先我们讲所有可能出现的点拿出来,也就是 \(S\) 集合中点对的 \(lca\) ,以及 \(S\) 本身,我们称这些点为关键点,他们构成了一个集合 \(T\) 。
-
我们将所有点按照他们的 \(dfs\) 序进行排序,然后相邻两个求 \(lca\) 就是所有点对的 \(lca\) 了。
不知道 \(dfs\) 序能看看我 这篇博客 。
接下来我们证明一下为什么这样就是对的。
证明:
如果有点对 \((x, y)\) 排序后不是相邻点对,他们的 \(lca\) 必然出现在别的里面。
如图所示
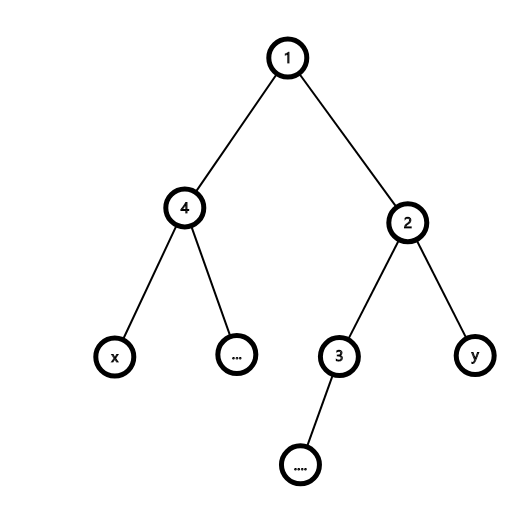
\(x, y\) 的 \(lca\) 为 \(1\) ,那么选择一个 \(dfs\) 序最大且在 \(dfs\) 序在 \(x\) 后面的 \(4\) 的子树的点 \(a\),
不难发现 \(a\) 的 \(dfs\) 序下一个点只能存在与 \(2\) 的子树当中,而这一对的 \(lca\) 为 \(1\) ,就已经包括了 \(x, y\) 的 \(lca\) 。
同理,就算不存在 \(a\) ,我们用 \(x\) 来替代 \(a\) 也能达到相同的效果。
其他情况全都可以类比论证,那么证毕。
怎么觉得证得很伪啊 -
然后将这些点再按 \(dfs\) 序排序,然后用
std :: unqiue去重。 -
用一个栈维护一条从根下来的关键点链,然后不断对于这个栈进行操作,每次将新加进来的点与栈顶连一条边。
因为是按照 \(dfs\) 序进行排序,所以一条链上的点是按照从高到低一个个出现的。
- 每次假设进来一个点 \(x\) ,我们把这个点与栈顶进行比较,如果 \(x\) 在栈顶点的子树中,连一条边我们就可以直接入栈。
- 否则我们一直弹掉栈顶元素,直至满足上面的要求(或者栈为空)
判断是否在子树中,我们可以记一下这个点进来的时间戳(也就是他的 \(dfs\) 序)
pre[u]以及离开的时间戳post[u]如果这个post[u] >= pre[v],那么意味着 \(v\) 在 \(u\) 的子树中。(因为有按pre排序的前提)这个过程可以形象地理解成有一条链从左往右不断在晃,然后每个点只需要连上他在这条链的父亲就行了。
代码
形象地看看代码实现吧qwq。。(其实很短)并且因为已经有了顺序,此处可以只加单向边了~
但需要注意的是,我们常常要把原来的点和新产生的 \(lca\) 进行区分,这个我们一开始打上标记就行了。
void Build() {
sort(lis + 1, lis + k + 1, Cmp);
for (int i = k; i > 1; -- i) lis[++ k] = Get_Lca(lis[i], lis[i - 1]);
sort(lis + 1, lis + k + 1, Cmp); k = unique(lis + 1, lis + k + 1) - lis - 1;
for (int i = 1; i <= k; ++ i) {
while (top && post[sta[top]] < pre[lis[i]]) -- top;
if (top) add_edge(sta[top], lis[i]); sta[++ top] = lis[i];
}
}
应用
对于每次只拿一些特殊点出来,然后对于这些点进行 \(dp\) 或者其他神奇操作的题。
虚树常常是解决这些题的利器。但要注意点数和 \(\sum k\) 不能很大。
它的构建的复杂度是 \(O((\sum k) \times \log n)\) 的,常数也不大。
题目
LOJ #2219. 「HEOI2014」大工程
题意
给你一棵有 \(n\) 个点的树,有 \(q\) 次询问,每次给你 \(k\) 个点,然后两两都有一条通道。
询问这 \(\displaystyle \binom {k}{2}\) 条通道中:
- 他们的距离和
- 他们之中距离最小的是多少
- 他们之中距离最大的是多少
\(n \le 10^6, \sum k \le 2 \times n\)
题解
每次考虑把那些点拿出来构造出虚树。
注意此处那些虚树的边权要换成原树中对应的那条链的边权和。(也就是两个 \(u, v\) 的深度之差)
然后我们就转化成求树上最长链,最短链,以及所有链长度之和。
前面两个可以利用一个很容易的 \(dp\) 来解决。
首先考虑最长链,具体来说令 \(f_u\) 为 \(u\) 向下延伸的最长链,\(f'_u\) 为 \(u\) 向下延伸的次长链。
然后最长链就是 \(\max \{f_u + f'_u\}\) 。
其实这个 \(f'_u\) 并不需要显式地记下来,只需要每次转移上来的时候和原来的 \(f_u\) 算一遍,然后尝试着更新即可。
最短链也是同理的。
然后对于所有链长度之和,这个很类似于 Wearry 当初出的那道题 [HAOI2018]苹果树 。
我们仍然是考虑一条边的贡献,它的贡献是边两边的子树点的乘积,再乘上这条边的边权。
然后就可以顺便记一下子树中关键点个数,然后转移就可以了qwq
复杂度是 \(O((\sum k) \log n)\)
代码
/**************************************************************
Problem: 3611
User: zjp_shadow
Language: C++
Result: Accepted
Time:4436 ms
Memory:204588 kb
****************************************************************/
#include <bits/stdc++.h>
#define For(i, l, r) for(register int i = (l), i##end = (int)(r); i <= i##end; ++i)
#define Fordown(i, r, l) for(register int i = (r), i##end = (int)(l); i >= i##end; --i)
#define Set(a, v) memset(a, v, sizeof(a))
#define Cpy(a, b) memcpy(a, b, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define DEBUG(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
typedef long long ll;
inline bool chkmin(ll &a, ll b) {return b < a ? a = b, 1 : 0;}
inline bool chkmax(ll &a, ll b) {return b > a ? a = b, 1 : 0;}
inline int read() {
int x = 0, fh = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') fh = -1;
for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
return x * fh;
}
void File() {
#ifdef zjp_shadow
freopen ("3611.in", "r", stdin);
freopen ("3611.out", "w", stdout);
#endif
}
const ll inf = 1e18;
const int N = 2e6, M = N << 1;
int Head[N], Next[M], to[M], val[M], e = 0;
inline void add_edge(int u, int v, int w) {
to[++ e] = v; Next[e] = Head[u]; val[e] = w; Head[u] = e;
}
inline void Add(int u, int v, int w) {
add_edge(u, v, w); add_edge(v, u, w);
}
#define Travel(i, u, v) for(register int i = Head[u], v = to[i]; i; v = to[i = Next[i]])
int dep[N], sz[N], fa[N], son[N];
void Dfs_Init(int u = 1, int from = 0) {
sz[u] = 1; dep[u] = dep[fa[u] = from] + 1;
Travel(i, u, v) if (v != from) {
Dfs_Init(v, u), sz[u] += sz[v];
if (sz[son[u]] < sz[v]) son[u] = v;
}
}
int top[N], pre[N], post[N];
void Dfs_Part(int u = 1) {
static int clk = 0; pre[u] = ++ clk;
top[u] = son[fa[u]] == u ? top[fa[u]] : u;
if (son[u]) Dfs_Part(son[u]);
Travel(i, u, v) if (v != fa[u] && v != son[u]) Dfs_Part(v);
post[u] = clk;
}
inline int Get_Lca(int x, int y) {
for (; top[x] != top[y]; x = fa[top[x]])
if (dep[top[x]] < dep[top[y]]) swap(x, y);
return dep[x] < dep[y] ? x : y;
}
inline bool Cmp(const int &a, const int &b) {
return pre[a] < pre[b];
}
ll Sum, Min, Max;
namespace Virtual_Tree {
bitset<N> Tag;
void Init() {
Tag.reset(); Set(Head, 0); e = 0;
Sum = 0; Min = inf, Max = -inf;
}
int lis[N * 2], cnt = 0, k;
void Build() {
cnt = k = read();
For (i, 1, k) Tag[lis[i] = read()] = true;
sort(lis + 1, lis + k + 1, Cmp);
For (i, 1, k - 1) lis[++ k] = Get_Lca(lis[i], lis[i + 1]); lis[++ k] = 1;
sort(lis + 1, lis + k + 1, Cmp); k = unique(lis + 1, lis + k + 1) - lis - 1;
static int Top, sta[N * 2]; Top = 0;
For (i, 1, k) {
while (Top && post[sta[Top]] < pre[lis[i]]) -- Top;
if (Top) add_edge(sta[Top], lis[i], dep[lis[i]] - dep[sta[Top]]); sta[++ Top] = lis[i];
}
}
void Clear() {
For (i, 1, k) Tag[lis[i]] = false, Head[lis[i]] = 0; e = 0;
Sum = 0; Min = inf, Max = -inf;
}
ll minv[N], maxv[N];
int Dp(int u = 1) {
int tot;
if (Tag[u]) tot = 1, minv[u] = maxv[u] = 0;
else tot = 0, minv[u] = inf, maxv[u] = -inf;
Travel(i, u, v) {
ll tmp = Dp(v); tot += tmp; Sum += 1ll * val[i] * (cnt - tmp) * tmp;
tmp = minv[v] + val[i]; chkmin(Min, minv[u] + tmp); chkmin(minv[u], tmp);
tmp = maxv[v] + val[i]; chkmax(Max, maxv[u] + tmp); chkmax(maxv[u], tmp);
}
return tot;
}
}
int main() {
File();
int n = read();
For (i, 1, n - 1) {
int u = read(), v = read(); Add(u, v, 0);
}
Dfs_Init(); Dfs_Part();
Virtual_Tree :: Init();
for (int m = read(); m; -- m) {
Virtual_Tree :: Build(); Virtual_Tree :: Dp();
printf ("%lld %lld %lld\n", Sum, Min, Max);
Virtual_Tree :: Clear();
}
return 0;
}
BZOJ 2286: [SDOI 2011]消耗战
题意
给你 \(n\) 个点以 \(1\) 为根的树,每条边有边权 \(w\) 。
有 \(q\) 次询问,每次询问 \(k\) 个点,问这些点与根节点断开的最小代价。
题解
显然又把这些关键点拿出来建出虚树。
然后我们可以用一个很显然的 \(dp\) 来解决,
令 \(f_u\) 为 \(u\) 子树中所有关键点到根的路径断掉最小代价。
为了方便转移,我们令 \(val_u\) 为 \(u\) 到根节点路径上边权最小值,这个显然可以预处理。
如果这个点是一个关键点,那么显然有 \(f_u = val_u\) ,因为必选向上最小的边,而下面的边选的话只会增大代价。
如果这个点不是关键点,那么就有 \(f_u = \min \{\sum_{v} f_v, val_u\}\) (此处 \(v\) 是 \(u\) 在虚树上的儿子)
这样就可以做完啦qwq
复杂度是 \(O((\sum k)\log n)\) 的。
代码
自己写吧qwq 很好写的。。。
。。。。。。
LOJ #2496. 「AHOI / HNOI2018」毒瘤
题意
给你一个有 \(n\) 个点 \(m\) 条边的联通图,求它的独立集数量。
\(n \le 10^5, n - 1 \le m \le n + 10\)
题解
一道好题。
可惜考试时候连状压都没调出来,暴力滚粗啦TAT 可惜可惜真可惜
首先考虑树的时候怎么做,令 \(f_{u, 0/1}\) 为 \(u\) 选与不选对于 \(u\) 的子树的方案数。
然后显然有
我们再考虑多了那些边如何处理,不难发现就是这些边连着的点(关键点)不能同时选择。
所以对于这些点就有三种状态 \((0, 0), (0, 1), (1, 0)\) 。
这样可以直接暴力枚举这些状态,然后到这些点的时候强制使这些关键点的 \(f_{u, 0/1} = 0~or~1\) 。
不难发现 \((0, 0)\) 和 \((0, 1)\) 可以合并到一起(强制使得前面那个点不选)
令 \(S = m - (n - 1)\) 。
然后这个直接做就是 \(O(2 ^ S \times n)\) ,期望得分 \(75\sim 85pts\) 。
然后不难发现这个可以使用虚树进行优化,因为每次的关键点是比较少的。
我们可以考虑把这个关键点对应的虚树建出来,然后为了方便,一开始就把这些点对应的虚树建出来就行了。
我们可以在 Dfs_Init() 中预处理出这个虚树,只需要考虑它有至少有两个子树都有关键点,那么它就是一个关键点。
不难发现这个关键点个数最多只有 \(4S\) 个。然后我们相当于把树上一些链合并成了一条边,然后对于剩下的点进行 \(dp\) 。
不难发现我们可以把 \(u, v\) 这两个点的关系表示成 \(k_{0/1,0/1}\) 也就是 \(f_{v,0/1}\) 对于 \(f_{u,0/1}\) 的贡献系数。
我们就可以考虑一开始处理出这个贡献系数。
我们令 \(g_{u,0/1}\) 为 \(u\) 不考虑它虚子树的方案数,这个转移和上面 \(f\) 的转移是类似的。
如果当前考虑的 \(v\) 是虚子树的话,分两种情况。
- \(u\) 是一个关键点,我们考虑连上 \(v\) 子树中的那个最高的关键点,边权就是之前的那个系数。
- \(u\) 不是一个关键点,那么继承 \(v\) 的转移系数(此处转移和 \(g\) 转移类似)
然后遍历完它所有儿子后,如果 \(u\) 是关键点,把它的 \(k\) 清空,重新为下一条链做准备。
如果不是的话,注意要把 \(g\) 乘到 \(k\) 上去。(因为这部分系数需要转移到后面去)
代码
建议看看代码,加强码力QwQ
#include <bits/stdc++.h>
#define For(i, l, r) for(register int i = (l), i##end = (int)(r); i <= i##end; ++i)
#define Fordown(i, r, l) for(register int i = (r), i##end = (int)(l); i >= i##end; --i)
#define Set(a, v) memset(a, v, sizeof(a))
#define Cpy(a, b) memcpy(a, b, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define DEBUG(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
inline bool chkmin(int &a, int b) {return b < a ? a = b, 1 : 0;}
inline bool chkmax(int &a, int b) {return b > a ? a = b, 1 : 0;}
inline int read() {
int x = 0, fh = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') fh = -1;
for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
return x * fh;
}
void File() {
#ifdef zjp_shadow
freopen ("2496.in", "r", stdin);
freopen ("2496.out", "w", stdout);
#endif
}
int n, m;
const int Mod = 998244353;
typedef long long ll;
typedef pair<ll, ll> PLL;
#define fir first
#define sec second
#define mp make_pair
inline PLL operator + (const PLL &a, const PLL &b) {
return mp((a.fir + b.fir) % Mod, (a.sec + b.sec) % Mod);
}
inline PLL operator * (const PLL &a, const int b) {
return mp(a.fir * b % Mod, a.sec * b % Mod);
}
inline PLL operator * (const PLL &a, const PLL b) {
return mp(a.fir * b.fir % Mod, a.sec * b.sec % Mod);
}
inline void operator *= (PLL &a, const int &b) { a = a * b; }
inline void operator += (PLL &a, const PLL &b) { a = a + b; }
inline ll Calc(PLL a, PLL b) {
PLL tmp = a * b; return (tmp.fir + tmp.sec) % Mod;
}
const int N = 1e5 + 1e3, M = N << 1;
PLL val0[M], val1[M];
struct Graph {
int Head[N], Next[M], to[M], e;
Graph() { e = 0; }
void add_edge(int u, int v, PLL wa = mp(0, 0), PLL wb = mp(0, 0)) {
to[++ e] = v; Next[e] = Head[u]; val0[e] = wa; val1[e] = wb; Head[u] = e;
}
} G1, G2;
#define Travel(i, u, v, G) for(register int i = G.Head[u], v = G.to[i]; i; i = G.Next[i], v = G.to[i])
ll g[N][2], f[N][2]; PLL k[N][2];
bitset<N> key, vis;
int Build(int u = 1) {
g[u][0] = g[u][1] = 1;
int son = 0; vis[u] = true;
Travel(i, u, v, G1) if (!vis[v]) {
int to = Build(v);
if (!to) {
(g[u][0] *= (g[v][0] + g[v][1])) %= Mod,
(g[u][1] *= g[v][0]) %= Mod;
}
else if (key[u])
G2.add_edge(u, to, k[v][0] + k[v][1], k[v][0]);
else
k[u][0] = k[v][0] + k[v][1],
k[u][1] = k[v][0], son = to;
}
if (key[u]) k[u][0] = mp(1, 0),
k[u][1] = mp(0, 1);
else k[u][0] *= g[u][0],
k[u][1] *= g[u][1];
return key[u] ? u : son;
}
int dfn[N], lv[N], rv[N], cnt = 0;
int Dfs_Init(int u = 1, int fa = 0) {
static int clk = 0; int tot = 0; dfn[u] = ++ clk;
Travel(i, u, v, G1) if (v != fa) {
if (!dfn[v]) tot += Dfs_Init(v, u);
else {
key[u] = true;
if (dfn[u] < dfn[v])
lv[++ cnt] = u, rv[cnt] = v;
}
}
key[u] = key[u] || (tot > 1);
return tot || key[u];
}
bool Shall[N][2]; ll dp[N][2];
void Dp(int u = 1) {
if(Shall[u][1]) dp[u][0] = 0; else dp[u][0] = g[u][0];
if(Shall[u][0]) dp[u][1] = 0; else dp[u][1] = g[u][1];
Travel(i, u, v, G2) {
Dp(v); PLL tmp = mp(dp[v][0], dp[v][1]);
(dp[u][0] *= Calc(val0[i], tmp)) %= Mod;
(dp[u][1] *= Calc(val1[i], tmp)) %= Mod;
}
}
int main () {
File();
n = read(); m = read();
For (i, 1, m) {
int u = read(), v = read();
G1.add_edge(u, v); G1.add_edge(v, u);
}
Dfs_Init(); key[1] = true; Build();
ll ans = 0;
For (sta, 0, (1 << cnt) - 1) {
For (i, 1, cnt)
if ((sta >> (i - 1)) & 1)
Shall[lv[i]][1] = Shall[rv[i]][0] = true;
else
Shall[lv[i]][0] = true;
Dp(); (ans += dp[1][1] + dp[1][0]) %= Mod;
For (i, 1, cnt)
if ((sta >> (i - 1)) & 1)
Shall[lv[i]][1] = Shall[rv[i]][0] = false;
else
Shall[lv[i]][0] = false;
}
printf ("%lld\n", ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号