图
1. 学习总结
1.1图的思维导图

1.2图结构学习体会
①深度优先遍历:从图中某个初始顶点v出发,首先访问初始顶点v,然后选择一个与顶点v相邻且没有被访问过的顶点w为初始顶点,再从w出发进行深度优先遍历,直到图中与当前顶点v邻接的所有顶点都被访问过为止。深度优先遍历的一个递归的过程。
②广度优先遍历:首先访问初始顶点v,接着访问顶点v的所有未被访问过的邻接点v1,v2…,然后按照v1,v2…的次序,访问每个顶点的所有未被访问过的邻接点,以此类推,直到图中所有和初始顶点相通的顶点都被访问过。
③Prim和Kruscal算法:Prim算法是一种构造性算法,Kruscal算法是一种按权值的递增顺序选择合适的边来构造最小生成树的方法。根据Kruskal算法的特性可得,在边越少的情况下,Kruskal算法相对Prim算法的优势就越大。
④Dijkstra算法:是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。不能解决最长路径的问题。
⑤拓扑排序算法:在一个有向图中找一个拓扑序列的过程。可以用于判断一个图中是否存在回路。
2.PTA实验作业
2.1.1 题目1:7-2 排座位
2.1.2 设计思路:
1和2是朋友,2和3是朋友。1和3之间就连通了,题目说朋友的朋友也是朋友,所以1和3也是朋友。我们用数组a[]表示下标对应的下一个点多少。每个点都有自己的下一个点。当下一个点没有了,找不到了,他就是最后一个点,所有的点只要能找到最后这个点的都是朋友。
2.1.3 代码截图

2.1.4 PTA提交列表说明
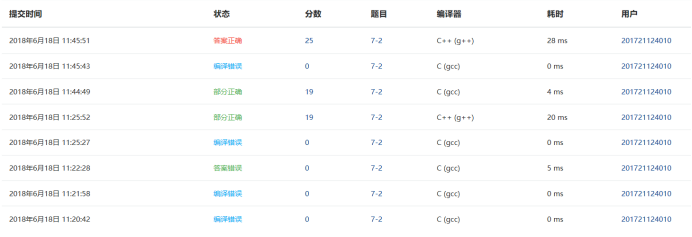
①答案错误:他们并不是朋友的状态没有考虑到他们还存在敌对状态都输出OK。
②部分正确:改进了上述错误,但是在最大N全连通环和最大N最大M全查询时发生错误。后来查了网络上这道题并查集的解法才全部正确。
2.2.1 题目2:7-1 图着色问题
2.2.2 设计思路:
用一个二维数组代表两个顶点和他们之间的边。创建两个分别存编号为i的点的颜色号和用来检查该种颜色是否是新出现的颜色的数组,若颜色数超过给定就不用判断下去直接输出no。接下来如果查到有不符合条件的边,或者方案中使用的颜色种类不是k种,说明该方案不可行,否则就可行。
2.2.3 代码截图

2.2.4 PTA提交列表说明

多种错误:刚开始想用图的广度优先遍历来判断是否相邻顶点用了相同颜色,但是在写的过程中用了比较复杂的邻接表形式存储图,而且也没有判断颜色数是否超过给定,因此多种错误。后来跟同学讨论后发现了较为简单的完成办法。
2.3.1 题目:7-4 公路村村通
2.3.2 设计思路:用prim算法求出城镇图的最小生成树,题目所给预算即图中每条边的权重。最小生成树的总权重就是最省预算。
2.3.3 代码截图

2.3.4 PTA提交列表说明
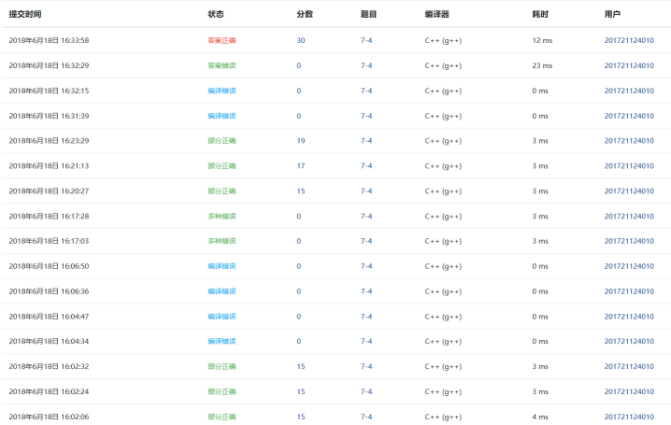
部分正确:没有考虑到当边的数量小于连通图最少需要的边数或者图不连通时,直接不存在最小生成树的情况,所以没有全部正确。后来仔细阅读了题目,再结合查阅的一些资料,得出了正确答案。
3. 截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分:1.5分
4. 阅读代码
/*
注意注意注意!!!
相同距离最短取最少结点
相同时间最少取最短路程
搞混了然后弄了好长时间。。。。。
然后例如vis_t, vis_d、sum_d, sum_node、dis_t, dis_d等
两个数组可以分别只用一个数组表示
*/
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
int Map_d[510][510];
int Map_t[510][510];
int pre_d[510];
int pre_t[510];
int vis_d[510];
int vis_t[510];
int sum_d[510];
int sum_node[510];
int dis_d[510];
int dis_t[510];
int M, N, S, D;
void Path(int pre[510], int i)
{
if(pre[i] == i)
return;
else
Path(pre, pre[i]);
printf("%d => ", pre[i]);
}
int cmp(int pre_a[150], int pre_b[150], int i)
{
if(pre_a[i] != pre_b[i])
return -1;
else if(pre_a[i] == pre_b[i] && pre_a[i] == i)
return 1;
else
cmp(pre_a, pre_b, pre_a[i]);
}
void Dijk_d()//相同距离最短取最少结点
{
int mind, mini;
for(int i = 0; i < N; ++i)
{
vis_d[i] = 0;
sum_node[i] = 0;
pre_d[i] = i;
dis_d[i] = inf;
}
vis_d[S] = 1;
dis_d[S] = 0;
for(int i = 0; i < N; ++i)
{
mind = inf, mini = S;
for(int j = 0; j < N; ++j)
{
if(vis_d[j] == 0 && mind > dis_d[j])
{
mini = j;
mind = dis_d[j];
}
}
vis_d[mini] = 1;
for(int j = 0; j < N; ++j)
{
/*
这里dis[mini]不能用mind代替, 因为当i = 0时
mini = S, mind = def 而实际的mind = dis[mini] = 0;
*/
if(vis_d[j] == 0 && dis_d[j] > dis_d[mini] + Map_d[mini][j])
{
dis_d[j] = dis_d[mini] + Map_d[mini][j];
pre_d[j] = mini;
sum_node[j] = sum_node[mini] + 1;
}
else if(vis_d[j] == 0 && dis_d[j] == dis_d[mini] + Map_d[mini][j])
{
if(sum_node[j] > sum_node[mini] + 1)
{
pre_d[j] = mini;
sum_node[j] = sum_node[mini] + 1;
}
}
}
}
}
void Dijk_t()//相同时间最少取最短路程
{
int mind, mini;
for(int i = 0; i < N; ++i)
{
vis_t[i] = 0;
sum_d[i] = 0;
//sum_node[i] = 0;
pre_t[i] = i;
dis_t[i] = inf;
}
vis_t[S] = 1;
dis_t[S] = 0;
for(int i = 0; i < N; ++i)
{
mind = inf, mini = S;
for(int j = 0; j < N; ++j)
{
if(vis_t[j] == 0 && mind > dis_t[j])
{
mini = j;
mind = dis_t[j];
}
}
vis_t[mini] = 1;
for(int j = 0; j < N; ++j)
{
/*
这里dis[mini]不能用mind代替, 因为当i = 0时
mini = S, mind = def 而实际的mind = dis[mini] = 0;
*/
if(vis_t[j] == 0 && dis_t[j] > dis_t[mini] + Map_t[mini][j])
{
dis_t[j] = dis_t[mini] + Map_t[mini][j];
pre_t[j] = mini;
sum_d[j] = sum_d[mini] + Map_d[mini][j];
}
else if(vis_t[j] == 0 && dis_t[j] == dis_t[mini] + Map_t[mini][j])
{
if(sum_d[j] > sum_d[mini] + Map_d[mini][j])
{
pre_t[j] = mini;
sum_d[j] = sum_d[mini] + Map_d[mini][j];
}
}
}
}
}
int main()
{
int minti, mindi, mind, mint;
scanf("%d %d", &N, &M);
for(int i = 0; i < N; ++i)
for(int j = 0; j < N; ++j)
if(i == j)
{
Map_t[i][j] = Map_d[i][j] = 0;
}
else
{
Map_t[i][j] = Map_d[i][j] = inf;
}
for(int i = 0; i < M; ++i)
{
int v1, v2, flag, len, time;
scanf("%d %d %d %d %d", &v1, &v2, &flag, &len, &time);
Map_t[v1][v2] = time;
Map_d[v1][v2] = len;
if(!flag)
{
Map_t[v2][v1] = time;
Map_d[v2][v1] = len;
}
}
scanf("%d %d", &S, &D);
Dijk_t();
Dijk_d();
// printf("******%d \n", sum_node[D]);
if(cmp(pre_t, pre_d, D) == 1)
{
printf("Time = %d; Distance = %d: ", dis_t[D], dis_d[D]);
Path(pre_t, D);
printf("%d\n", D);
}
else
{
printf("Time = %d: ", dis_t[D]);
Path(pre_t, D);
printf("%d\n", D);
printf("Distance = %d: ", dis_d[D]);
Path(pre_d, D);
printf("%d", D);
}
}




