【JZOJ1900】【2010集训队出题】矩阵 （经典2-SAT问题）

题意

有一个\(n*n\)的矩阵\(B\)，一个\(1*n\)的矩阵\(C\)，你现在要构造一个\(1*n\)的\(0/1\)矩阵，令\((A*B-C)*A^T=D\)，\(D\)只有一个元素，你要使得这个元素值最大。
\(n\leq 600\)

分析

推一下矩阵乘法的式子就能转换为这样的问题：

有\(n\)个元素编号为\(1 \sim n\)，选择\(i\)将获得\(-c_i\)的贡献，同时选择\(i,j\)将获得\(b_{i,j}\)的贡献，找出一种方案使得贡献最大。

这是一个典型的2-SAT问题，建模方法如下：

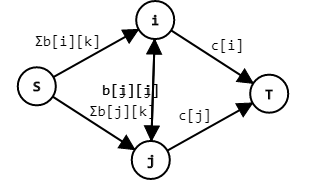
建立源点\(S\)，向中间一排\(n\)个点连边，边权为\(\sum b_{i,k}\)，这些边存在的意义是\(a_i=1\)。中间一排点向汇点\(T\)连边，边权为\(c_i\)，这些边存在的意义是\(a_i=0\)。中间的点两两连边，边权为\(b_{i,j}\)。

思考这个网络的最小割的意义。对于中间某个点\(i\)，显然\((S,i)\)和\((i,T)\)两条边有且仅有一条被割，割\((S,i)\)意义为\(a_i=0\)，割\((i,T)\)意义为\(a_i=1\)。当\(a_i,a_j\)有一个为\(0\)时，必定存在\(S,i,j,T\)的路径，\(b_{i,j}\)这条边就会割掉，贡献就会减去。综上，这个网络的最小割就对应原模型的解。

Code

#include <cstdio>
#include <cstring>

const int N = 617, INF = 2147483647;
inline int read()
{
	int x = 0, f = 0;
	char c = getchar();
	for (; c < '0' || c > '9'; c = getchar()) if (c == '-') f = 1;
	for (; c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) + (c ^ '0');
	return f ? -x : x;
}
int min(int a, int b) { return a < b ? a : b; }

int n;
int ans, b[N][N], c[N];

int tot = 1, st[N], to[N * N * 4], nx[N * N * 4], len[N * N * 4], gap[N];
int cur[N];
void add(int u, int v, int w)
{
	to[++tot] = v, nx[tot] = st[u], len[tot] = w, st[u] = tot;
	to[++tot] = u, nx[tot] = st[v], len[tot] = 0, st[v] = tot;
}

int S, T, h, t, q[N], dep[N];
void bfs()
{
	memset(dep, -1, sizeof(dep));
	memset(gap, 0, sizeof(gap));
	h = 1, q[t = 1] = T, dep[T] = 0;
	while (h <= t)
	{
		int u = q[h++];
		++gap[dep[u]];
		for (int i = st[u]; i; i = nx[i]) if (dep[to[i]] == -1) dep[to[i]] = dep[u] + 1, q[++t] = to[i];
	}
}
int dinic(int u, int flow)
{
	if (u == T) return flow;
	int rest = flow, tmp;
	for (int i = cur[u]; i; i = nx[i])
	{
		cur[u] = i;
		if (len[i] > 0 && dep[u] == dep[to[i]] + 1)
		{
			tmp = dinic(to[i], min(rest, len[i]));
			len[i] -= tmp, len[i ^ 1] += tmp, rest -= tmp;
			if (!rest) return flow;
		}
	}
	--gap[dep[u]];
	if (gap[dep[u]] == 0) dep[S] = n + 3;
	++dep[u];
	++gap[dep[u]];
	return flow - rest;
}

int main()
{
	//freopen("matrix.in", "r", stdin);
	n = read();
	for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) b[i][j] = read(), ans += b[i][j];
	for (int i = 1; i <= n; i++) c[i] = read();
	S = 0, T = n + 1;
	for (int i = 1; i <= n; i++)
	{
		int s = 0;
		for (int j = 1; j <= n; j++) s += b[i][j];
		add(S, i, s), add(i, T, c[i]);
	}
	for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) if (i != j) add(i, j, b[i][j]);
	bfs();
	while (dep[S] < n + 2) memcpy(cur, st, sizeof(st)), ans -= dinic(S, INF);
	printf("%d\n", ans);
	return 0;
}