树的重心(模板)
代码定义:树的重心也叫树的质心。对于一棵树n个节点的无根树,找到一个点,使得把树变成以该点为根的有根树时,最大子树的结点数最小。换句话说,删除这个 [1] 点后最大连通块(一定是树)的结点数最小。
性质:
-
树中所有点到某个点的距离和中,到重心的距离和是最小的,如果有两个距离和,他们的距离和一样。
-
把两棵树通过一条边相连,新的树的重心在原来两棵树重心的连线上。
-
一棵树添加或者删除一个节点,树的重心最多只移动一条边的位置。
-
一棵树最多有两个重心,且相邻。
算法分析:
和树的最大独立问题类似,先任选一个结点作为根节点,把无根树变成有根树,然后设d(i)表示以i为根的子树的结点的个数。不难发现d(i)=∑d(j)+1,j∈s(i)。s(i)为i结点的所有儿子结点的编号的集合。程序也十分简单:只需要DFS一次,在无根树有根数的同时计算即可,连记忆化都不需要——因为本来就没有重复计算。
那么,删除结点i后,最大的连通块有多少个呢?结点i的子树中最大有max{d(j)}个结点,i的“上方子树”中有n-d(i)个结点
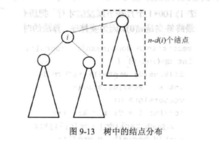
代码:
#include<iostream> #include<vector> #include<cstdio> #include<cstring> using namespace std; typedef long long ll; const int maxn=200005; vector<int> tree[maxn]; int n,minNode,minBalance; //minNode当前重心节点 //minBalance当前重心节点的最大子树节点个数 int d[maxn]; //d[i]表示以i为根的子树节点个数 void dfs(int u,int fa){ d[u]=1; //节点本身 int maxSub=0,size=tree[u].size(); //maxSub为节点u的最大子树节点个数 for(int i=0;i<size;i++){ int v=tree[u][i]; if(v!=fa){ dfs(v,u); d[u]+=d[v]; maxSub=max(maxSub,d[v]); } } maxSub=max(maxSub,n-d[u]); if(maxSub<minBalance){ minNode=u; minBalance=maxSub; } } int main(){ int t; cin>>t; while(t--){ cin>>n; for(int i=1;i<=n;i++) tree[i].clear(); memset(d,0,sizeof(d)); for(int i=1;i<n;i++){ int u,v; cin>>u>>v; tree[u].push_back(v); tree[v].push_back(u); } minNode=0; minBalance=0x3f3f3f3f; dfs(1,0); printf("%d %d\n",minNode,minBalance); } return 0; }




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步